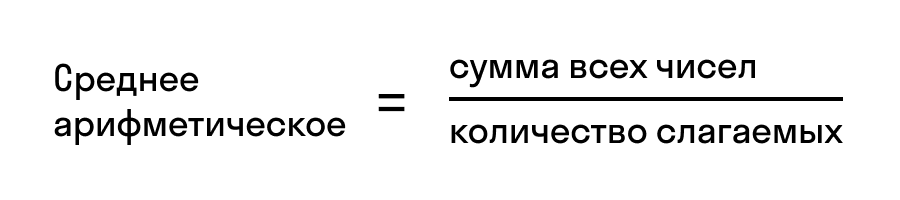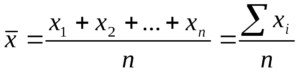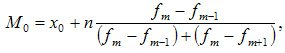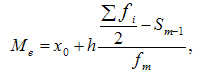Что называют средним арифметическим нескольких чисел 5 класс

3 простых формулы, чтобы посчитать среднее арифметическое

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие среднего арифметического

Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Вот так:

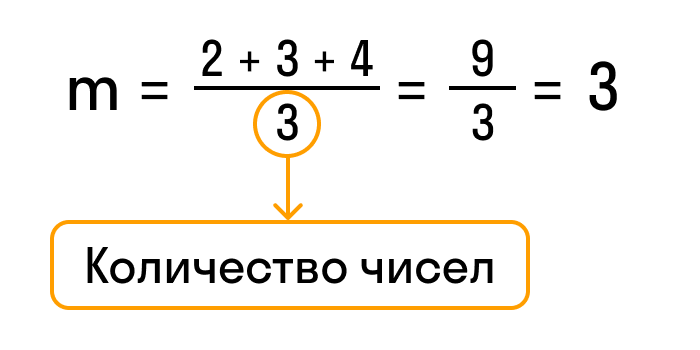
Например, найдем среднее арифметическое чисел 5, 6 и 7. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.

Разделим результат на количество чисел в задании, то есть на три.

Так получилась формула среднего арифметического:

Способы вычисления среднего арифметического

Стандартная формула. Чтобы найти среднее арифметическое, нужно сложить все числа и поделить эту сумму на их количество. Формула выглядит так:

Вычисление моды или наиболее часто встречающегося значения. Формула такая:

Вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. Если такого значения нет, за медиану принимают среднее число между границами половин выборки. Формула выглядит так:

Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: в магазине, на работе, в диалоге с другом или во время презентации перед инвесторами. Еще пригодятся, чтобы рассчитать среднюю скорость движения.

Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:

Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.

Примеры расчета среднего арифметического

Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.

Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.

Пример 2. Посчитать среднее арифметическое 7,5 и 8 и 0,5.

Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.

Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.

Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.

Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.

Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.

Ответ: школьник в неделю тратит в среднем 81 рубль.

В 5 классе можно искать среднее арифметическое с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Источник

Мерзляк 5 класс — § 36. Среднее арифметическое. Среднее значение величины

Вопросы к параграфу

1. Что называют средним арифметическим нескольких чисел?

Средним арифметическим чисел называют частное от деления суммы этих чисел на количество слагаемых.

2. Приведите примеры средних значений величин.

Часто используются следующие средние величины:

Решаем устно

1. Заполните цепочку вычислений:

2. Найдите четвёртую часть разности 5,2 — 2,4.

3. Найдите пятую часть произведения 1,8 • 1,5.

(1,8 • 1,5) : 5 = 1,8 • (1,5 : 5) = 1,8 • 0,3 = 0,54

5. От села до станции 2 км. Успеет ли пешеход на поезд, если выйдет из села за 0,6 ч до отхода поезда и будет двигаться со скоростью 2,5 км/ч?

2,5 • 0,6 = 1,5 (км) — можно пройти за 0,6 ч при скорости движения 2,5 км/ч.

Ответ: пешеход не успеет.

Упражнения

1033. Найдите среднее арифметическое чисел:

1) 10,3 и 9,1

(10,3 + 9,1) : 2 = 19,4 : 2 = 9,7

2) 2,8; 16,9 и 22

(2,8 + 16,9 + 22) : 3 = 41,7 : 3 = 13,9

1034. Найдите среднее арифметическое чисел:

1) 4,2 и 2,1

(4,2 + 2,1) : 2 = 6,3 : 2 = 3,15

2) 3,9; 6; 9,18 и 15,8

(3,9 + 6 + 9,18 + 15,8) : 4 = 34,88 : 4 = 8,72

1035. В течение недели в 8 ч утра Саша измерял температуру воздуха. Он получил такие результаты: 20 °С; 18 °С; 16 °С; 15 °С; 14 °С; 17 °С; 19 °С. Найдите среднее значение проведённых измерений.

(20 + 18 + 16 + 15 + 14 + 17 + 19) : 7 = 119 : 7 = 17 ( °С) — средняя температура воздуха в 8 ч утра.

1036. Найдите среднюю оценку по математике учащихся вашего класса за II четверть. Ответ округлите до единиц.

Для этого надо сложить все оценки учащихся классы, выставленные за II четверть, затем разделить полученное число на количество учащихся и округлить его до единиц.

Например, в классе 10 учеников, которые за II четверть получили оценки: 4, 5, 5, 3, 3, 4, 3, 5, 5, 5. Рассчитаем среднее арифметическое:

(4 + 5 + 5 + 3 + 3 + 4 + 3 + 5 + 5 + 5) : 10 = (4 • 2 + 5 • 5 + 3 • 3) : 10 = (8 + 25 + 9) : 10 = 42 : 10 = 4,2 ≈ 4.

Значит средняя оценка по математике — 4.

1037.1) Поезд ехал 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч. Найдите среднюю скорость поезда на протяжении всего пути.

1) 64 • 4 = 256 (км) — проехал поезд в первый отрезок времени.

2) 53,2 • 5 = 266 (км) — проехал поезд во второй отрезок времени.

3) 256 + 266 = 522 (км) — проехал поезд всего.

4) 4 + 5 = 9 (часов) — двигался поезд всего.

5) 522 : 9 = 58 (км/ч) — средняя скорость поезда.

2) В автомастерской работает 10 человек. У двоих из них месячная зарплата составляет 22 800 р., у четверых — 28 000 р., у троих 31 000 р., а у одного 32 000 р. Какова средняя зарплата работников мастерской?

(22 800 • 2 + 28 000 • 4 + 31 000 • 3 + 32 000) : 10 = 282 600 : 10 = 28 260 (рублей) — средняя месячная зарплата работников.

Ответ: 28 260 рублей.

1038.1) Автомобиль ехал 3 ч со скоростью 56,4 км/ч и 4 ч со скоростью 62,7 км/ч. Найдите среднюю скорость автомобиля на всём пути.

1) 56,4 • 3 = 169,2 (км) — проехал автомобиль в первый отрезок времени.

2) 62,7 • 4 = 250,8 (км) — проехал автомобиль во второй отрезок времени.

3) 169,2 + 250,8 = 420 (км) — проехал автомобиль всего.

4) 3 + 4 = 7 (часов) — двигался автомобиль всего.

5) 420 : 7 = 60 (км/ч) — средняя скорость автомобиля.

2) Фермер собрал с каждого гектара поля площадью 30 га по 30,2 ц пшеницы, а с каждого гектара поля площадью 20 га — по 32,3 ц пшеницы. Какой средний урожай с одного гектара собрал фермер?

1) 30,2 • 30 = 906 (ц) — собрали с первого поля.

2) 32,3 • 20 = 646 (ц) — собрали со второго поля.

3) 906 + 626 = 1552 (ц) — собрали всего.

4) 30 + 20 = 50 (га) — площадь двух полей.

5) 1552 : 50 = 31,04 (ц/га) — средняя урожайность.

1039.Среднее арифметическое чисел 7,8 и х равно 7,2. Найдите х.

(7,8 + х) : 2 = 7,2
7,8 + х = 7,2 • 2
7,8 + х = 14,4
х = 14,4 — 7,8
х = 6,6

1040.Среднее арифметическое чисел 6,4 и у равно 8,5. Найдите у.

(6,4 + у) : 2 = 8,5
6,4 + у = 8,5 • 2
6,4 + у = 17
у = 17 — 6,4
у = 10,6

1041.Среднее арифметическое двух чисел, одно из которых в 4 раза меньше второго, равно 10. Найдите эти числа.

Пусть первое число равно х, тогда второе число равно 4х. Составим уравнение:

(х + 4х) : 2 = 10
5х : 2 = 10
5х = 10 • 2
5х = 20
х = 20 : 5
х = 4 — первое число.

4 • 4 = 16 — второе число.

Ответ: первое число равно 4, а второе число равно 16.

1042.Среднее арифметическое двух чисел, одно из которых на 4,6 больше второго, равно 8,2. Найдите эти числа.

Пусть первое число равно х, тогда второе число равно (х — 4,6). Составим уравнение:

(х + (х — 4,6)) : 2 = 8,2
(2х — 4,6) : 2 = 8,2
2х — 4,6 = 8,2 • 2
2х — 4,6 = 16,4
2х = 16,4 + 4,6
2х = 21
х = 21 : 2
х = 10,5 — первое число.

10,5 — 4,6 = 5,9 — второе число.

Ответ: первое число 10,5, а второе число 5,9.

1043. Отметьте на координатном луче числа а и b и их среднее арифметическое, если:

1) а = 2, b = 6

с = (2 + 6) : 2 = 8 : 2 = 4 — среднее арифметическое.

2) а = 4, b = 7

с = (4 + 7) : 2 = 11 : 2 = 5,5 — среднее арифметическое.

Как расположена точка, соответствующая среднему арифметическому чисел а и b, относительно точек, соответствующих числам а и b?

Точка, соответствующая среднему арифметическому, расположена ровно посередине между точками а и b.

1044.Принимая участие в математической олимпиаде, Дима решил 10 задач. За каждую задачу он мог получить не более 12 баллов. За первые восемь задач мальчик получил среднюю оценку 7 баллов. Сколько баллов получил Дима за каждую из оставшихся двух задач, если среднее количество баллов за одну задачу составляло 8 баллов?

1) 8 • 10 = 80 (баллов) — получил Дима всего.

2) 7 • 8 = 56 (баллов) — получил Дима за первые 8 задач.

3) 80 — 56 = 24 (балла) — получил Дима за 9-ю и 10-ю задачу.

4) 24 : 2 = 12 (баллов) — средний бал за последние две задачи.

Так как, по условию, Дима не мог получить за задачу более 12 баллов, то оценка двух последних задач равна среднему баллу за них, а именно 12 баллам.

Ответ: за 9-ю и 10-ю задачу Дима получил по 12 баллов.

1045.Автомобиль ехал 3,4 ч по шоссе со скоростью 90 км/ч и 1,6 ч по грунтовой дороге. С какой скоростью ехал автомобиль по грунтовой дороге, если средняя скорость на протяжении всего пути составляла 75,6 км/ч?

1) 3,4 + 1,6 = 5 (часов) — всего двигался автомобиль.

2) 75,6 • 5 = 378 (км) — всего проехал автомобиль.

3) 3,4 • 90 = 306 (км) — проехал автомобиль по шоссе.

4) 378 — 306 = 72 (км) — проехал автомобиль по грунтовой дороге.

5) 72 : 1,6 = 45 (км/ч) — скорость автомобиля по грунтовой дороге.

1046.Купили 2 кг конфет одного вида по 255 р. за килограмм, 4 кг конфет второго вида по 285 р. за килограмм и ещё 3 кг конфет третьего вида. Средняя цена купленных конфет составляла 260 р. за килограмм. Сколько стоил килограмм конфет третьего вида?

1) 255 • 2 = 510 (р) — заплатили за конфеты первого вида.

2) 285 • 4 = 1 140 (р) — заплатили за конфеты второго вида.

3) 1 140 + 510 = 1 640 (р) — заплатили за конфеты первых двух видов.

4) 2 + 4 + 3 = 9 (кг) — конфет купили всего.

5) 260 • 9 = 2340 (р) — заплатили за все конфеты.

6) 2340 — 1650 = 690 (р) — заплатили за конфеты третьего вида.

7) 690 : 3 = 230 (р) — цена за кг конфет третьего вида.

1047. Среднее арифметическое четырёх чисел равно 2,1, а среднее арифметическое трёх других чисел — 2,8. Найдите среднее арифметическое этих семи чисел.

(2,1 • 4 + 2,8 • 3) : 7 = (8,4 + 8,4) : 7 = 16,8 : 7 = 2,4 — среднее арифметическое семи чисел.

Ответ: среднее арифметическое 2,4.

1048.Среднее арифметическое семи чисел равно 10,2, а среднее арифметическое трёх других чисел — 6,8. Найдите среднее арифметическое этих десяти чисел.

(10,2 • 7 + 6,8 • 3) : 10 = (71,4 + 20,4) : 10 = 91,8 : 10 = 9,18 — среднее арифметическое десяти чисел.

Ответ: среднее арифметическое 9,18.

1049. Средний возраст одиннадцати футболистов команды равен 22 годам. Во время игры одного из футболистов удалили с поля, после чего средний возраст оставшихся игроков составил 21 год. Сколько лет было футболисту, который покинул поле?

1) 22 • 11 = 242 (года) — суммарный возраст всех одиннадцати игроков команды.

2) 21 • 10 = 210 (лет) — суммарный возраст оставшихся десяти игроков команды.

3) 242 — 210 = 32 (года) — возраст удалённого игрока.

1050. На сколько среднее арифметическое всех чётных чисел от 1 до 1 000 включительно больше, чем среднее арифметическое всех нечётных чисел от 1 до 1 000 включительно?

1051.Семь гномов собрались вечером вокруг костра. Оказалось, что рост каждого гнома равен среднему арифметическому роста двух его соседей. Докажите, что все гномы были одного роста.

Упражнения для повторения

1052. Найдите числа, которых не хватает в цепочке вычислений:

1) a = 9,88 : 3,8 = 2,6

Ответ: a = 2,6; b =2,06; с = 3,5.

Ответ: x = 2,8; y = 2,74; z = 13,4.

1053.1) Периметр прямоугольника равен 36,8 см, а одна из его сторон — 13,8 см. Вычислите площадь прямоугольника.

Дано:

P = 36,8 см
a = 13,8 см

Найти:

Решение:

P = (a + b) • 2. Составим уравнение:

36,8 = (13,8 + b) • 2
13,8 + b = 36,8 : 2
13,8 + b = 18,4
b = 18,4 — 13,8
b = 4,6 (см) — длина второй стороны прямоугольника.

S = 13,8 • 4,6 = 63,48 (см²) — площадь прямоугольника.

2) Ширина прямоугольного параллелепипеда равна 7,2 см, что составляет 0,8 его длины и 0,18 его высоты. Вычислите объём параллелепипеда.

1) 7,2 : 8 • 10 = 0,9 • 10 = 9 (см) — длина прямоугольного параллелепипеда.

2) 7,2 : 18 • 100 = 0,4 • 100 = 40 (см) — высота прямоугольного параллелепипеда.

3) 9 • 7,2 • 40 = 360 • 7,2 = 2592 (см³) — объём прямоугольного параллелепипеда.

1054. В 25 банок разлили поровну 32 кг мёда. Сколько мёда налили в каждую банку? Ответ округлите до десятых.

32 : 25 = 1,28 (кг) ≈ 1,3 (кг) — мёда налили в каждую банку.

Задача от мудрой совы

1055.Одновременно на сковороду можно положить двух карасей. Чтобы поджарить одного карася с одной стороны, нужна 1 мин. Можно ли за 3 мин поджарить с двух сторон трёх карасей?

Да, если действовать следующим образом:

Источник

Среднее арифметическое. Среднее значение величины

Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на количество слагаемых.

Говоря о значениях каких − то величин, часто имеют в виду их средние значения. Например, когда говорят, что с 1 га поля собрали 38 ц пшеницы, то это не означает, что с каждого гектара поля было собрано именно такое количество центнеров пшеницы. Эту величину получили, разделив массу всего урожая, выраженную в центнерах, на площадь всего поля, выраженную в гектарах. Величина 38 ц является средней урожайностью с 1 га данного поля.

Еще один пример. Если автомобиль проехал 120 км за 1,5 ч, то, разделив длину пути на время, получим среднюю скорость движения автомобиля. Она равна 80 км/ч. При этом автомобиль мог останавливаться, ехать со скоростью большей либо меньшей, чем 80 км/ч.

Средний возраст футболиста команды, средняя за один матч результативность футболиста, среднее количество молока, потребляемое одним жителем России в год, и т.п. также являются примерами средних величин.

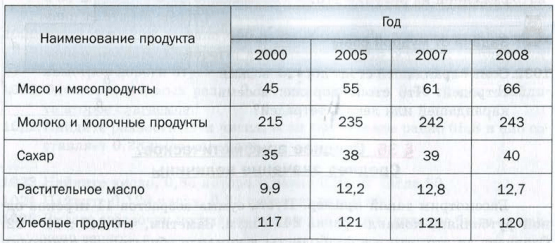
В повседневной жизни мы часто встречаемся со средними значениями величин. Например, приведем таблицу потребления некоторых продуктов питания в России (в килограммах на человека в год).

Такую таблицу могут использовать, например, экономисты и диетологи в своих исследованиях, крупные производители и поставщики сельхозпродукции при планировании своей деятельности.

1 ) 54 * 4 = 216 (км) − проехал автомобиль со скоростью 54 км/ч.

2 ) 60 * 2 = 120 (км) − проехал автомобиль со скоростью 60 км/ч.

3 ) 216 + 120 = 336 (км) − весь путь, пройденный автомобилем.

4 ) 4 + 2 = 6 (ч) − общее время движения автомобиля.

5 ) 336 : 6 = 56 (км/ч) − средняя скорость движения автомобиля.

1 ) 2,4 + 3,6 = 6 (кг) − печенья купила мама.

2 ) 73 * 6 = 438 (р.) − стоит все печенье.

3 ) 55 * 2,4 = 132 (р.) − стоит печенья первого вида.

4 ) 438 − 132 = 306 (р.) − стоит печенье второго вида.

5 ) 306 : 3,6 = 85 (р.) − цена 1 кг печенья второго вида.

Источник

Урок математики в 5 классе «Среднее арифметическое нескольких чисел»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

ПЛАН-КОНСПЕКТ УРОКА
Среднее арифметическое нескольких чисел

Мурашова Людмила Петровна

МАОУ «СОШ №26 с углубленным изучением химии и биологии

Тема и номер урока в теме

Среднее арифметическое нескольких чисел (первый урок из пяти по данной теме).

Цель урока: формировать представление о среднем арифметическом нескольких чисел; познакомить учащихся с правилом нахождения среднего арифметического и его использованием при решении несложных задач.

— образовательные ( формирование познавательных УУД ) :

научить в процессе реальной ситуации использовать определения следующих понятий: «среднее арифметическое нескольких чисел», «правило нахождения среднего арифметического»

— воспитательные ( формирование коммуникативных и личностных УУД ) :

умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

— развивающие ( формирование регулятивных УУД )

умение обрабатывать информацию и ранжировать ее по указанным основаниям; представлять информацию в табличной форме, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

10.Тип урока Урок первичного предъявления новых знаний.

11.Формы работы учащихся: Фронтальная, парная, индивидуальная

12.Организация деятельности учащихся на уроке:

-самостоятельно выходят на проблему и решают её;

-самостоятельно определяют тему, цели урока;

-выводят определение и правило среднего арифметического нескольких чисел;

-работают с текстом учебника;

-работают с технологической картой при выполнении заданий;

-отвечают на вопросы;

-решают самостоятельно задачи;

-оценивают себя и друг друга;

13. Необходимое техническое оборудование: Компьютер, проектор, интерактивная доска, учебники по математике, раздаточный материал (технологическая карта, карточки с дополнительным заданием, карточки с домашним заданием), электронная презентация, выполненная в программе Power Point

14.Структура и ход урока

Название используемых ЭОР

(с указанием действий с ЭОР, например, демонстрация)

Источник

Среднее арифметическое чисел. Мода. Медиана. Размах ряда чисел

Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.

Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.

Например: найдем среднее арифметическое чисел 2; 6; 9; 15.

У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.

Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.

Например: найдем размах чисел 2; 5; 8; 12; 33.

Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.

Мода ряда чисел – это число, которое встречается в данном ряду чаще других.

Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.

Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.

Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.

Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.

В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.

Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?

Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

Найдите медиану и размах ряда.

Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

Найдите моду ряда и среднее арифметическое ряда.

Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.

Найдите среднюю заработную плату.

Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.

Найдите разность среднего арифметического и медианы этого набора.

Найдите объем и медиану числового ряда.

Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:

Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.

Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.

Найдите среднее арифметическое этого набора чисел.

Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.

Найдите медиану этого набора чисел.

Провели несколько измерений случайной величины:

800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.

Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.

Найдите разность среднего арифметического и медианы этого набора.

Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.

Найдите среднее арифметическое, размах и моду.

Источник