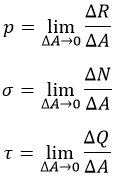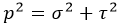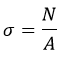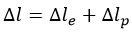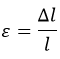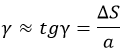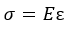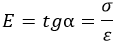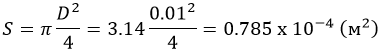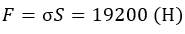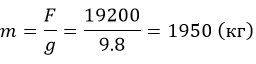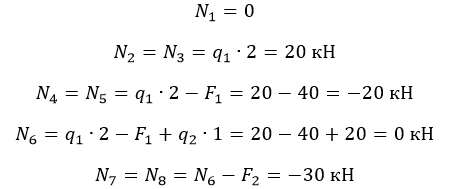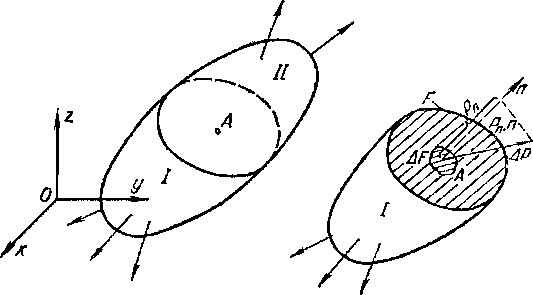Что называют сопротивлением материалов
iSopromat.ru
Сопротивление материалов
Сопротивление материалов (сокр. — сопромат) — это инженерная наука, изучающая методы расчёта элементов машин и сооружений на прочность, жесткость и устойчивость для обеспечения их надежной и безопасной эксплуатации.
Другими словами, сопромат — это грамотное проектирование конструкций.
Сопромат — наука о прочности
С точки зрения сопромата, машины и сооружения должны быть прочными и надежными, но при этом желательно, чтобы они были как можно легче и дешевле.
Видео о том, что такое сопромат и для чего он нужен:
Сопротивление материалов — раздел технической механики, в котором изучаются экспериментальные и теоретические основы и методы расчета наиболее распространенных элементов различных конструкций, находящихся под воздействием внешних нагрузок, на прочность, жесткость и устойчивость, с учетом требований надежности, экономичности, технологичности изготовления, удобства транспортировки и монтажа, а также безопасности при эксплуатации.
Сопротивление материалов является одной из фундаментальных дисциплин общеинженерной подготовки специалистов в сфере высшего технического образования.
База знаний для изучения сопромата
Студенты высших технических учебных заведений приступают к изучению дисциплины «Сопротивление материалов» после освоения курса теоретической механики. Кроме того необходимы базовые знания физики и высшей математики.
Основные характеристики и строение металлов рассматривается в курсе материаловедения.
Объект изучения
В сопромате главным объектом для расчета является брус, нагруженный системой внешних усилий (сил, моментов и распределенных нагрузок).
Для него могут проводится следующие виды расчетов:
Расчет на прочность является основным, т.к. абсолютно все конструкции должны быть прочными.
При расчетах на жесткость определяются деформации бруса и перемещение его сечений, на основании чего делается заключение о жесткости бруса. При невыполнении условия жесткости определяются необходимые размеры сечения.
Структура курса «Сопротивление материалов»
Курс сопротивления материалов в ВУЗах имеет, как правило, следующую структуру:
Изучение дисциплины включает выполнение расчетно-графических и лабораторных работ с последующей защитой, после чего студенты сдают экзамен.
Учебные материалы по сопромату
Для успешного освоения данного курса предлагаем следующие материалы для самостоятельного изучения:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Многочисленные учебники «Cопромат для чайников» создают для развенчания мифа о непостижимой сложности дисциплины. Этой наукой пугают на первых курсах вузов. Для начала расшифруем грозный термин «сопротивление материалов».
На деле – проста и решение почти не выходит за рамки школьной задачи о растяжении и сжатии пружины. Другое дело – найти слабое звено конструкции и свести расчет к несложной постановке. Так что не стоит зевать на лекциях по основам механики. При подготовке к урокам можно пользоваться решениями онлайн, но на экзаменах помогут только свои знания.
Что такое сопромат
Это методика расчета деталей, конструкций на способность выдерживать нагрузки в требуемой степени. Или хотя бы для предсказания последствий. Не более, хотя почему-то относят руководство к наукам.
Этой «наукой» прекрасно владели древнегреческие и древнеримские инженеры, сооружавшие сложнейшие механизмы. Понятия не имея о структуре, уравнении состояния вещества и прочих теориях, египтяне строили исполинские плотины и пирамиды.
Основные задачи по сопротивлению материалов
Задача следует напрямую из определения. А вот каковы критерии упомянутого слова «выдерживать»? Неясно, что скрывается под «материалом» и как реальные вещи схематизировать.
Требования
Перечислены далеко не все, но для статики и базовой программы хватит:
Прочность – способность образца воспринимать внешние силы без разрушения. Слегка мнущаяся под весом оборудования подставка никого не интересует. Основную-то функцию она выполняет.
Жесткость – свойство воспринимать нагрузку без существенного нарушения геометрии. Гнущийся под силой резания инструмент даст дополнительную погрешность обработки. К ошибке приведет деформация станины агрегата.
Устойчивость – способность конструкции сохранять стабильность равновесия. Поясним на примере: стержень находится под грузом, будучи прямым – выдерживает, а чуть изогнется – характер напряжения изменится, груз рухнет.
Материал и силы
Как всякая методика, сопромат принимает массу упрощений и прямо неверных допущений:
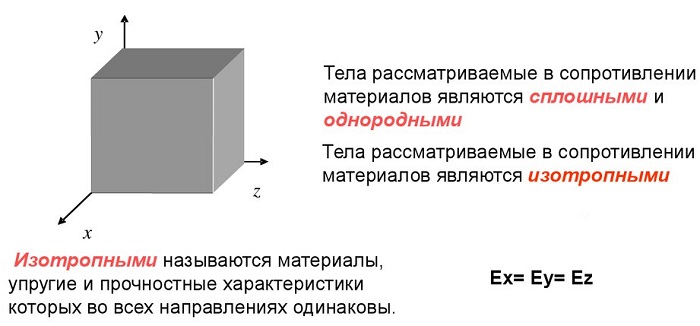
материал однороден, среда сплошная. Внутренние особенности в расчет не берутся;
свойства не зависят от направления;
образец восстанавливает начальные параметры при снятии нагрузки;
поперечные сечения не меняются при деформации;
в удаленных от места нагрузки местах усилие распределяется равно по сечению;
результат воздействия нагрузок равен сумме последствий от каждой;
деформации не влияют на точки приложения сил;
отсутствуют изначальные внутренние напряжения.
Схемы
Служат для создания возможности расчета реальных конструкций:
тело – объект с практически одинаковыми «длина х ширина х высота»;
брус (балка, стержень, вал) – характеризуется значительной длиной.
На рисунке показаны опоры с воспринимаемыми реакциями (обозначены красным цветом):
Рис. 1. Опоры с воспринимаемыми реакциями:
в) жесткая заделка (защемление).
Силы в сопромате
Приложенные извне, уравновешиваются возникающими изнутри. Напомним, рассматривается статическая ситуация. Материал «сопротивляется».
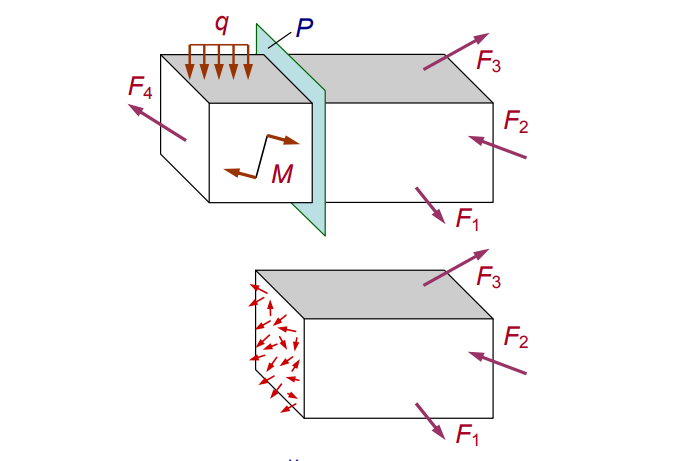
Разделим нагруженное тело виртуальным сечением P (см. рис. 2).
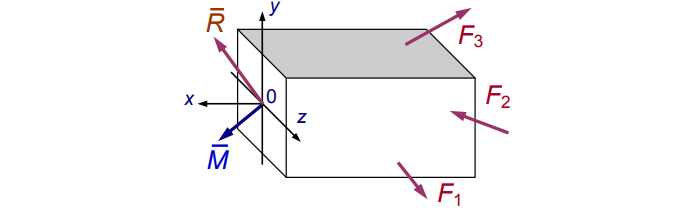
Заменим хаос равнодействующей R и моментом M (см. рис. 3):
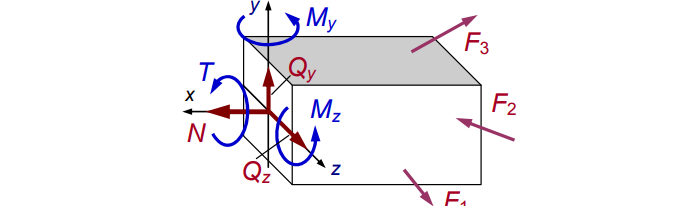
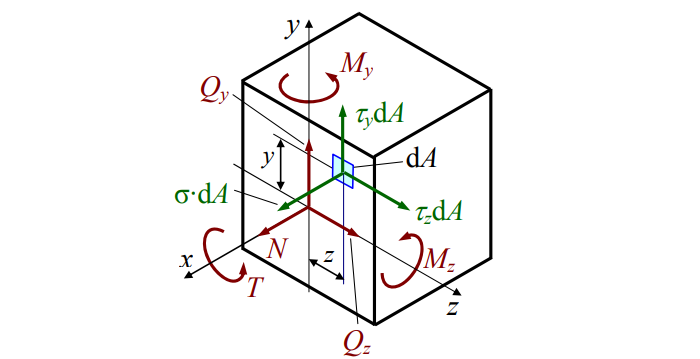
Распределив по осям, получим картину нагрузки сечения (см. рис. 4):
Нагрузки и деформации, изучаемые в сопромате
Изучим несколько принятых терминов.
Напряжения
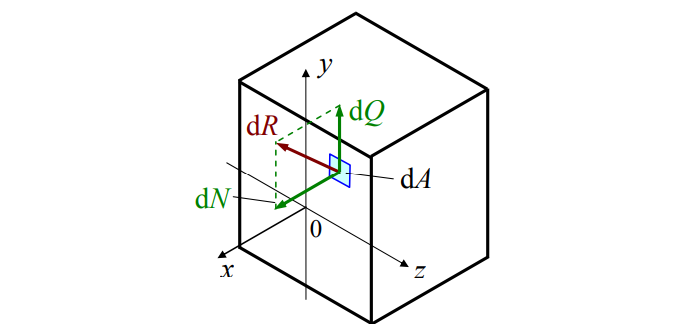
В теле приложенные силы распределяются по сечению. Нагружен каждый элементарный «кусочек». Разложим силы:
Элементарные усилия таковы:
σ – «сигма», нормальное напряжение. Перпендикулярно сечению. Характерно для сжатия / растяжения;
τ – «тау», касательное напряжение. Параллельно сечению. Появляется при кручении;
p – полное напряжение.
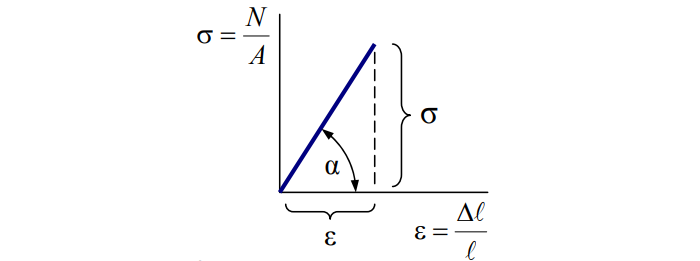
Просуммировав элементы, получим:
N – нормальная сила;
A – площадь сечения.
В принятой в России системе СИ сила измеряется в ньютонах (Н). Напряжения – в паскалях (Па). Длины в метрах (м).
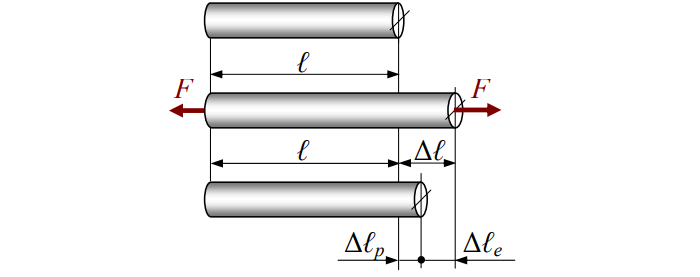
Деформации
Различают деформацию упругую (с индексом «e») и пластическую (с индексом «p»). Первая исчезает по снятии растягивающей / сжимающей силы, вторая – нет.
Полная деформация будет равна:
Деформация относительная обозначается «ε» и рассчитывается так:
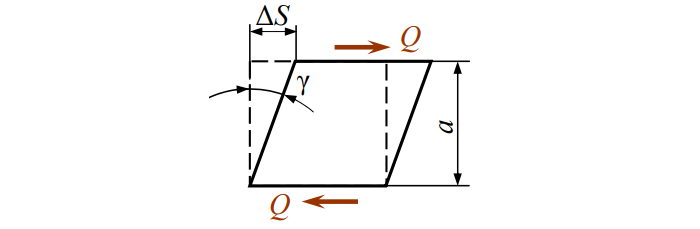
Под «сдвигом» понимается смещение параллельных слоев. Рассмотрим рисунок:
Здесь γ – относительный сдвиг.
Виды нагрузки
Растяжение и сжатие – нагрузка нормальной силой (по оси стержня).
Кручение – действует момент. Обычно рассчитываются передающие усилия валы.
Изгиб – воздействие направлено на искривление.
Основные формулы
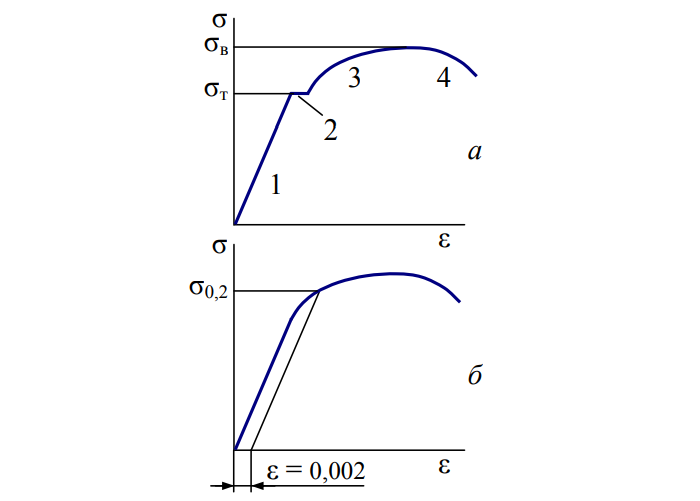
Базовый принцип сопромата единственный. В упомянутой задаче о пружине применим закон Гука:
E – модуль упругости (Юнга). Величина зависит от используемого материала. Для стали полагают равным 200 х 10 6 Па.
Сопротивление материала прямо пропорционально деформации:
Закон верен не всегда и не для всех материалов. Как уже упоминалось, принимается как одно из допущений.
Реальная диаграмма
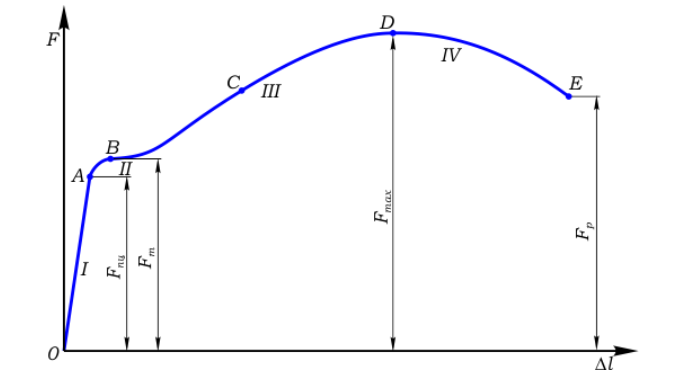
Растяжение стержня из низкоуглеродистой стали выглядит следующим образом:
График (б) относится к большей части конструкционных материалов: подкаленные стали, сплавы цветных металлов, пластики.
Расчеты обычно ведут по σт (а) и σ0.2 (б). С незначительными пластическими деформациями конструкции или без таковых.
Пример решения задачи
Какой груз допустимо подвесить на пруток из стали 45 Ø10 мм?
σ0,2 для стали 45 равна 245 МПа (из ГОСТ).
Площадь сечения прутка:
Допустимая сила тяжести:
Для получения веса следует разделить на ускорение свободного падения g:
Ответ: необходимо подвесить груз массой 1950 кг.
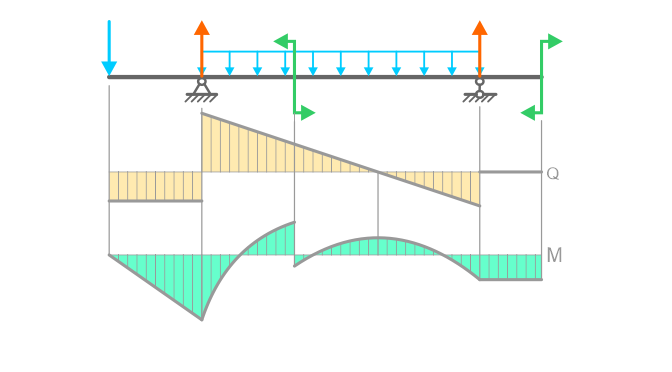
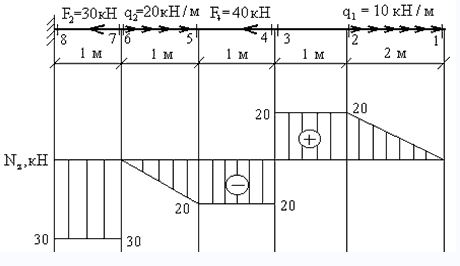
Как найти опасное сечение
Наиболее простой способ – построение эпюры. На закрепленную балку действуют точечные и распределенные силы. Считаем на характерных участках, начиная с незакрепленного конца.
Усилие положительно, если направлено на растяжение.
На схеме показано, что:
Зачем и кому нужен сопромат
Даже не имеющий отношения к прочностным расчетам инженер-универсал должен иметь понятие о приблизительных (на 10-20%) значениях. Знать конструкционные материалы, представлять свойства. Чувствовать заранее слабые места агрегатов.
Совершенно необходим разработчикам различных конструкций, машиностроительных изделий. Будущим архитекторам в вузах преподается в виде предмета «Строительная механика».
Методика помогает на стадии проектирования обеспечивать необходимый запас прочности изделий. Стойкость к постоянным и динамичным нагрузкам. Это сберегает массу времени и затрат в дальнейших изготовлении, испытании и эксплуатации изделия. Обеспечивает надежность и долговечность.
Сопротивление материалов
Сопротивление материалов (в обиходе — сопромат) — часть механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности. Сопротивление материалов относится к фундаментальным дисциплинам общеинженерной подготовки специалистов с высшим техническим образованием, за исключением специальностей, не связанных с проектированием объектов, для которых прочность является важным показателем.
Содержание
Определение
Сопротивление материалов базируется на понятии «прочность», что является способностью материала противостоять приложенным нагрузкам и воздействиям без разрушения. Сопротивление материалов оперирует такими понятиями как: внутренние усилия, напряжения, деформации. Приложенная внешняя нагрузка к некоторому телу порождает внутренние усилия в нём, противодействующие активному действию внешней нагрузки. Внутренние усилия, распределенные по сечениям тела называются напряжениями. Таким образом, внешняя нагрузка порождает внутреннюю реакцию материала, характеризующуюся напряжениями,которые в свою очередь прямо пропорциональны деформациям тела. Деформации бывают линейные такие как удлинение,укорочение, сдвиг и углы поворота сечений. Основные понятия сопротивления материалов оценивающие способность материала сопротивляться внешним воздействиям являются:
Связь с другими науками
В теоретической части сопротивление материалов базируется на математике и теоретической механике, в экспериментальной части — на физике и материаловедении и применяется при проектировании машин, приборов и конструкций. Практически все специальные дисциплины подготовки инженеров по разным специальностям содержат разделы курса сопротивления материалов, так как создание работоспособной новой техники невозможно без анализа и расчета её прочности, жёсткости и надёжности.
Задачей сопротивления материалов, как одного из разделов механики сплошной среды, является определение деформаций и напряжений в твёрдом упругом теле, которое подвергается силовому или тепловому воздействию.
Эта же задача среди других рассматривается в курсе теории упругости. Однако методы решения этой общей задачи в том и другом курсах существенно отличаются друг от друга. Сопротивление материалов решает её главным образом для бруса, базируясь на ряде гипотез геометрического или физического характера. Такой метод позволяет получить, хотя и не во всех случаях, вполне точные, но достаточно простые формулы для вычисления напряжений. Также поведением деформируемых твёрдых тел под нагрузкой занимается теория пластичности и теория вязкоупругости.
Гипотезы и допущения
Расчет конструкций и их элементов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов существует модель идеализированного деформируемого тела.
Эти положения ограниченно применимы к решению конкретных закдач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.
Теории прочности
Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупко и пластично. В зависимости от условий (например, температура, состояние напряжений, виды нагрузки) большинство материалов может быть отнесено к хрупким или пластичным или обоим видам одновременно. Тем не менее, для большинства практических ситуаций, материалы могут быть классифицированы как хрупкие или пластичные. Несмотря на то, что теория разрушения находится в разработке уже более 200 лет, уровень её приемлемости для механики сплошных сред, не всегда достаточен.
В математических терминах, теория разрушения выражается в виде различных критериев разрушения, которые справедливы для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение. Поэтому это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения.
Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:
1. Теория наибольших нормальных напряжений.
2. Теория наибольших деформаций.
3. Теория наибольших касательных напряжений Треска (Tresca).
4. Теория наибольшей удельной потенциальной энергии формоизменения фон Мизеса (von Mises).
Классические теории прочности имеют существенные ограничения для их применения. Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причём только для некоторых определённых условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона. Кулон (Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок. Математическая формулировка закона Кулона совпадает с теорией Мора, если в ней выразить главные напряжения через касательные и нормальные напряжения на площадке среза. Достоинством теории Мора является то, что она применима к материалам, имеющим разные сопротивления сжатию и растяжению, а недостатком то, что она учитывает влияние только двух главных напряжений — максимального и минимального. Поэтому теория Мора не точно оценивает прочность при трехосном напряженном состоянии, когда необходимо учитывать все три главных напряжения. Кроме того, при использовании эта теория не учитывается поперечное расширение (дилатацию) материала при сдвиге. На эти недостатки теории Мора неоднократно обращал внимание А. А. Гвоздев, который доказал неприменимость теории Мора для бетона [2].
На смену «классическим» теориям прочности в современной практике пришли многочисленные новые новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения:
Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчёта анизотропных материалов.
Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементов и вычислительной техники. При макро-моделировании предварительно выполняется гомогенизация — условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учётом их физических характеристик. Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий. Критерии разрушения каменных конструкций учитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму.
Применение
Методы сопротивления материалов широко используются при расчете несущих конструкций зданий и сооружений, в дисциплинах связанных с проектированием деталей машин и механизмов.
Как правило, именно из-за оценочного характера результатов, получаемых с помощью математических моделей этой дисциплины, при проектировании реальных конструкций все прочностные характеристики материалов и изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах).
В студенческой среде сопротивление материалов считается одной из наиболее сложных общепрофессиональных дисциплин, что дало богатую пищу студенческому фольклору и породило целый ряд шуток и анекдотов.
См. также
Литература
Лекция 1. Сопротивление материалов. Основные понятия и определения
Основные определения
Сопротивление материалов позволяет определить прочность, жесткость и устойчивость элементов строительных конструкций и деталей машин, тем самым обеспечить долгую и надежную работу сооружений, машин и механизмов.
Вещества и комбинации веществ, из которых состоят тела, и являются рассматриваемыми материалами. Все твердые тела по геометрической форме можно условно разделить на 3 группы:
Это можно выразить соотношением длины к высоте или ширине. Стержни можно условно разделить на 3 категории:
1.1. Стержни с соотношением l/h ≥ 10.
Таким образом линия, изображающая стержень на чертежах, совпадает с осью стержня. Часто ось стержня называется упругой линией, нейтральной линией или нейтральной осью.
при которых исключается возможность разрушения конструкции при действии заданных нагрузок. Другими словами напряжения, возникающие в рассматриваемых поперечных сечениях, не должны превышать расчетного сопротивления материала.
возникающих под действием заданных нагрузок. Так как не существует материалов, имеющих бесконечно большую жесткость, то деформации материала конструкции приводят к изменению геометрической формы элементов конструкции, а значит и к перераспределению внутренних напряжений.
при котором изменение первоначальной геометрической формы под действием нагрузок и возникающего при этом перераспределения внутренних напряжений не приводит к разрушению конструкции.
Деформации рассматриваются как перемещение точек, линий и плоскостей.
Линейная деформация измеряется в единицах длины.
относительно некоторой точки.
на рассматриваемом участке длины элемента конструкции.
остающиеся после снятия нагрузки.
Другими словами остаточные деформации, при упругой деформации равны нулю.
после снятия нагрузок.
Все материалы обладают определенными упругими и пластичными свойствами. Например изготовление профилированного листа из листа металлопроката происходит в результате накопления остаточных деформаций.
Если силы направлены по оси, то такой элемент конструкции называют центрально сжатым или центрально растянутым. Если силы приложены на некотором расстоянии от оси, то такой элемент называют внецентренно сжатым или внецентренно растянутым, при этом расстояние от оси до точки приложения силы называется эксцентриситетом е.
т.е. в плоскости поперечного сечения
т.е. в плоскости, перпендикулярной плоскости поперечного сечения.
Моменты могут быть крутящими и изгибающими. Момент, возникающий при внецентренном растяжении или сжатии, является изгибающим.
К изотропным материалам условно можно отнести металлы, камень, стекло.
Представителем такого материала является древесина.
Свойства анизотропных материалов не являются предметом рассмотрения теории сопротивления материалов. Между тем не существует природных или искусственных материалов, имеющих идеальную упругость, изотропию или отротропию. Кроме того изготовить конструкцию идеальной геометрической формы практически невозможно. Это означает, что для точных расчетов необходимо учитывать все изменения геометрической формы, а также возможные отклонения от заданных физико-механических свойств. Однако в подавляющем большинстве случаев для обеспечения надежной работы строительной конструкции, машины или механизма достаточно выполнить приближенный (упрощенный) расчет. Выполняется такой расчет на основании следующих допущений.
Основные допущения, принимаемые в теории сопротивления материалов
1. Рассматриваемый материал является изотропным (или ортотропным) и идеально упругим.
2. Деформации материала пропорциональны приложенной нагрузке, не превышающей некоторой предельной величины, т.е рассматриваемые тела являются линейно-деформируемыми.
3. При составлении уравнений равновесия деформациями материала можно пренебречь, так как деформации рассматриваемых элементов значительно меньше геометрических размеров элементов. В данном случае не только значительно меньше длины, но также высоты и ширины.
4. При расчетах допускается использовать принцип независимости действия сил, т.е. упругую деформацию под действием нескольких сил можно рассматривать как сумму упругих деформаций от каждой отдельно взятой силы.
5. Предполагается, что сечения которые были плоскими до приложения нагрузок, остаются плоскими при деформациях материала.
Внешние и внутренние силы
Все силы, действующие на тело, можно условно разделить на внешние и внутренние. Условно потому, что силы тяжести, действующие на каждую частицу тела, находятся как бы внутри тела, а внутренние силы (силы взаимодействия между элементарными частицами вещества) действуют и до того, как к телу приложена какая-либо внешняя сила.
Внешние силы по характеру приложения можно разделить на четыре вида:
Так как при расчетах изначально рассматривается ось стержня, не имеющая высоты и ширины, то объемные и плоские нагрузки часто приводятся к линейной. Это допускается делать без каких-либо поправочных коэффициентов, если интенсивность объемной или плоской нагрузки является постоянной.
В природе точечных нагрузок не существует. Любая нагрузка прикладывается к некоторой площади, но если площадь приложения нагрузки, точнее длина приложения нагрузки после приведения плоской нагрузки к линейной, значительно меньше длины тела, то такую нагрузку можно условно рассматривать, как сосредоточенную в одной точке. Переход от сосредоточенной нагрузки к равномерно распределенной и наоборот осуществляется только с помощью соответствующих коэффициентов.
По времени действия нагрузки делятся на постоянные и временные
Постоянные нагрузки, например, собственный вес конструкции, действуют в течение всего срока службы. Временные нагрузки ограничены по времени действия.
По характеру изменения во времени нагрузки делятся на статические и динамические
Статические нагрузки прикладываются как бы постепенно, поэтому инертные силы, возникающие при движении инертных масс, при расчетах не учитываются. Динамические нагрузки прикладываются очень быстро и потому при расчетах влияние инертных сил необходимо учитывать.
Все вышеприведенные нагрузки рассматриваются как активные.
Равнодействующую внутренних сил, действующую на рассматриваемую площадь, называют внутренним усилием.
Уравнения равновесия. Метод сечений
Кроме того, если рассечь тело в любом месте, то чтобы тело по-прежнему оставалось в состоянии равновесия к полученному сечению нужно приложить некоторую внешнюю силу Q. Значение внешней силы определяется, исходя из условий равновесия. А так как сила действия равна силе противодействия, то считается, что внутренние усилия Р или напряжения р, возникающие в результате действия внешних сил (нагрузок) равны по значению нагрузкам, приложенным в рассматриваемом сечении и направлены в противоположную сторону. Такой метод расчета и называется методом сечений.
Примечание: Для решения статически неопределимых задач одних только уравнений равновесия и уравнения моментов недостаточно.
Рисунок 317.1
Так как напряжения, возникающие в рассматриваемых сечениях под действием внешних сил, редко бывают равномерно распределенными (не имеют постоянной интенсивности), то для решения задач сопротивления материалов важно знать не просто значение внутренних усилий, но также и значение напряжений в наиболее опасных точках сечения. Отношение внутреннего усилия ΔР, действующего на некоторой площади ΔF рассматриваемого сечения будет приближаться к некоторому пределу, если площадь ΔF будет стремиться к нулю (к точке А). Этот предел, как мы выяснили ранее, называется напряжением и определяет интенсивность внутренних усилий, действующих на рассматриваемую площадку в точке А. Напряжения могут быть различны не только в разных точках одного сечения, но и в одной и той же точке А, общей для различных сечений, т.е. сечений, рассекающих тело под различными углами.
Ось, перпендикулярная плоскости сечения, называется нормалью.
Полное напряжение в точке А, имеющей координаты (х, у, z) для сечения с нормалью n определяется по формуле:

где ΔР — элементарное внутреннее усилие, возникающее при отбрасывании части II тела и замене этой части элементарной внешней силой ΔQ, действующей на оставшуюся часть I для соблюдения условий равновесия.
Нормальное напряжение σn действует в направлении нормали
Если усилие ΔР не перпендикулярно рассматриваемой плоскости сечения (как на рисунке 317.1), то значение нормального напряжения можно определить по формуле:

Касательное напряжение тn действует в плоскости сечения
Значение касательного напряжения можно определить по формуле:

дальше
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).