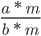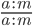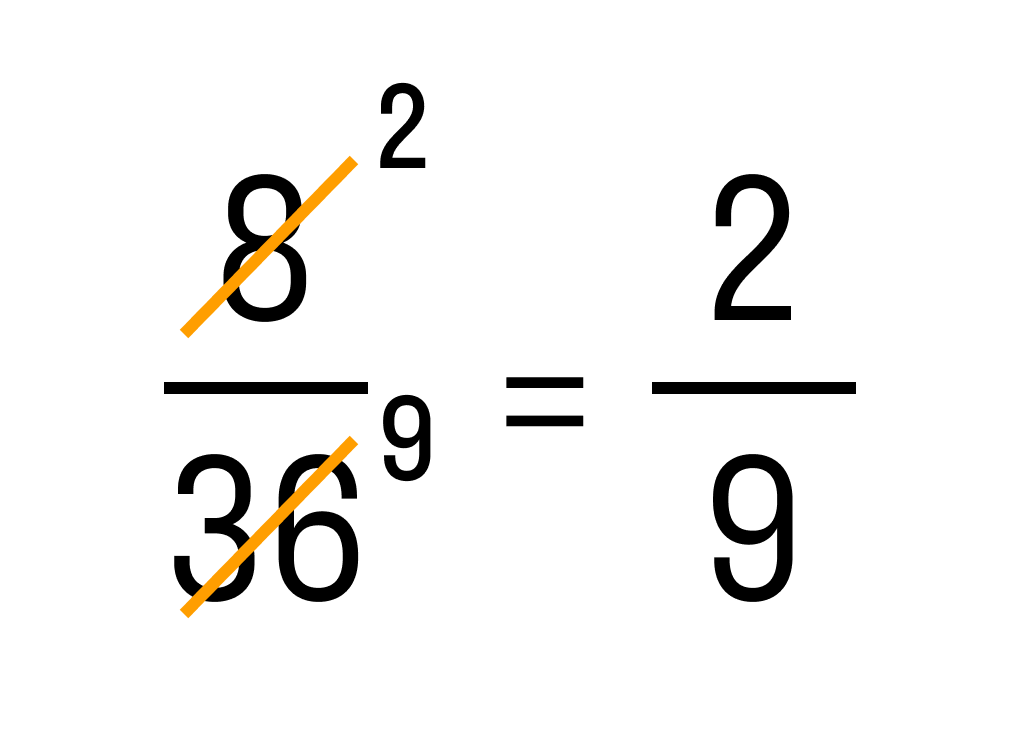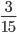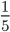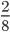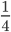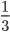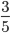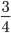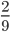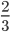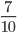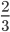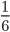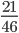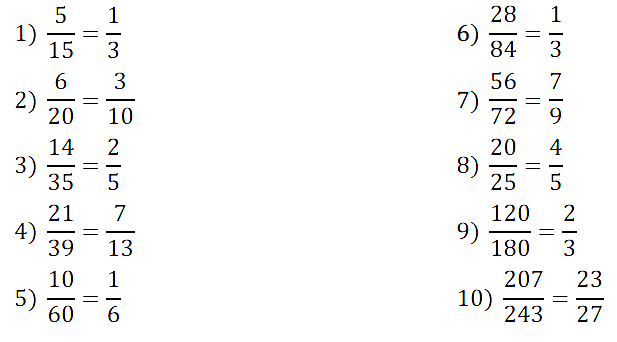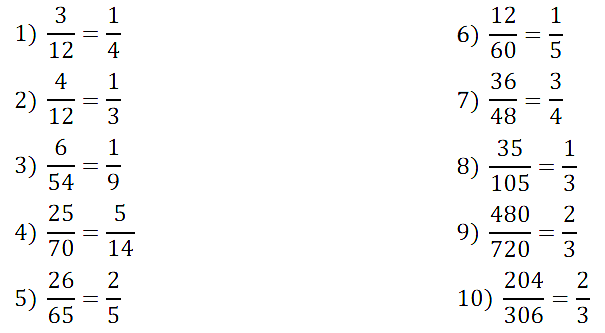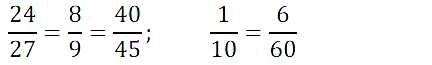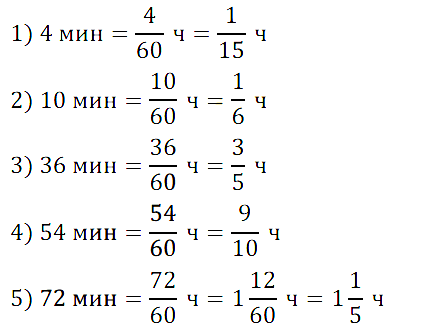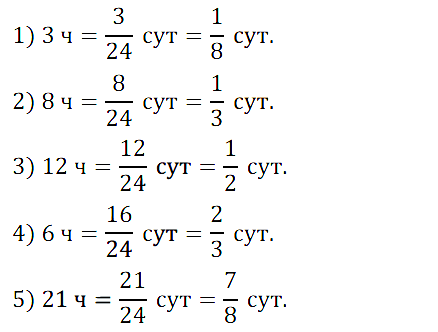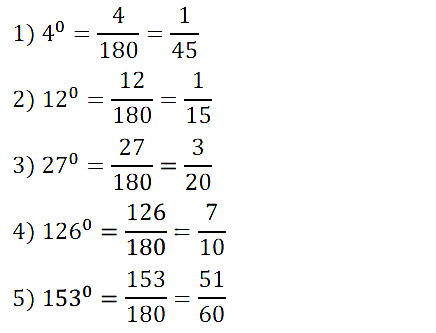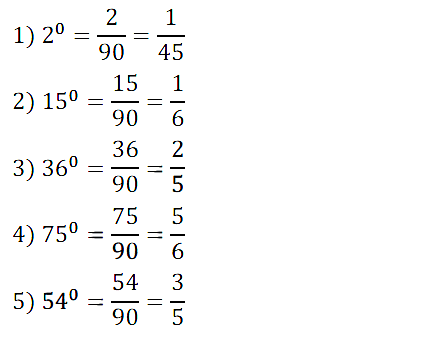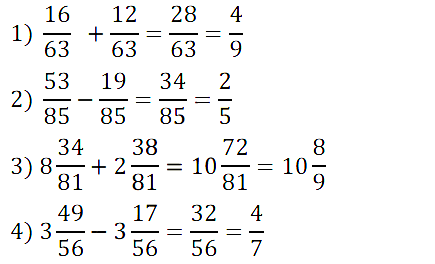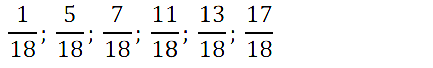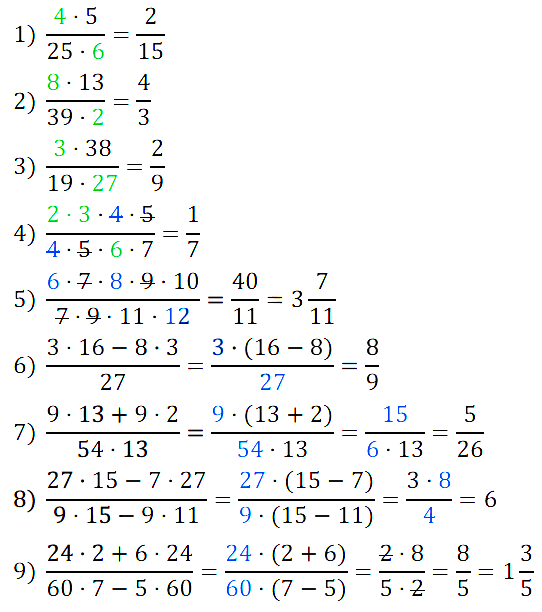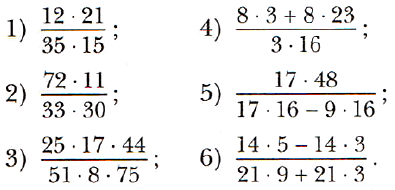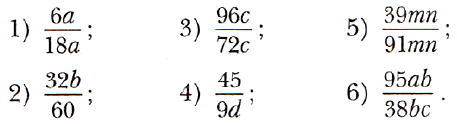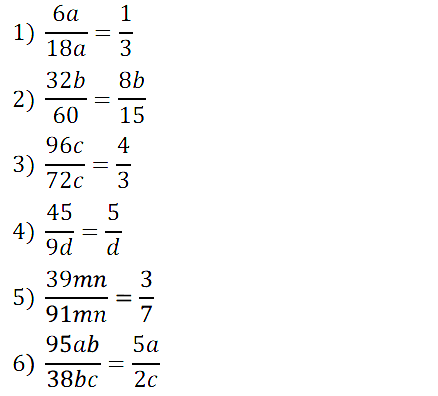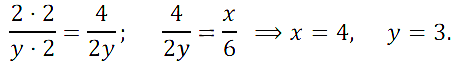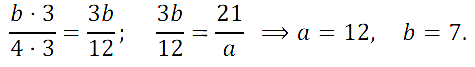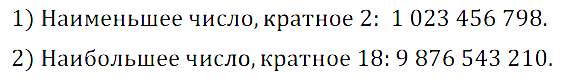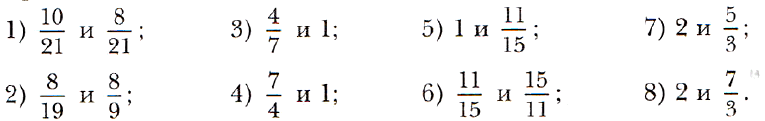Что называют сокращением дроби 6 класс мерзляк
Сокращение обыкновенных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:


где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Больше наглядных примеров и понятных объяснений — на курсах обучения математике в онлайн-школе Skysmart.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.

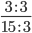
Сокращение выполнено: 
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.

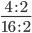
Сокращение выполнено: 
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби 
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
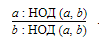
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1

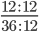
Сокращение выполнено: 
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
Найдем частное: 15 : 5 = 3

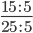
Сокращение выполнено: 
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.

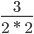
Сокращение выполнено: 
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9

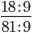
Сокращение выполнено: 
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:

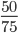
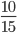
Сокращение выполнено: 
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

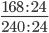
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

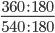
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

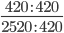
Сокращение выполнено. Дробь приведена к несократимому виду: 
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

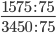
Сокращение выполнено. Дробь приведена к несократимому виду: 
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.
Математика 6 Мерзляк. Упражнения 210-235
Математика 6 класс Мерзляк
§ 8. Упражнения 210-235
№ 210. Сократите дробь: 1) 5/15, 2) 6/20, 3) 14/35, 4) 21/39, 5) 10/60, 6) 28/84, 7) 56/72, 8) 20/25, 9) 120/180, 10) 207/243.
Правильный ответ:
№ 211. Сократите дробь: 1) 3/12, 2) 4/12, 3) 6/54, 4) 25/70, 5) 26/65, 6) 12/60, 7) 36*48, 8) 35/105, 9) 480/720, 10) 204/306.
Правильный ответ:
№ 212. Какие из дробей 11/12, 7/42, 9/111, 5/42, 12/68, 13/36 несократимы?
Правильный ответ:
№ 213. Найдите среди дробей 15/25, 24/99, 28/45, 26/51, 16/42, 22/69 несократимые.
Правильный ответ:
№ 214. Запишите десятичную дробь в виде обыкновенной дроби и результат, если возможно, сократите: 1) 0,4; 3) 0,12; 5) 0,16; 7) 0,128; 9) 0,2348; 2) 0,5; 4) 0,84; 6) 0,59; 8) 0,96; 10) 0,975.
Правильный ответ:
№ 215. Найдите среди данных дробей равные между собой: 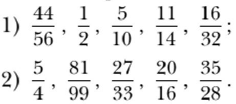
Правильный ответ:
№ 216. Найдите среди дробей 24/27, 1/10, 6/60, 8/9, 40/45 равные между собой и запишите соответствующие равенства.
Правильный ответ:
№ 217. Какую часть часа составляют: 1) 4 мин; 2) 10 мин; 3) 36 мин; 4) 54 мин; 5) 72 мин?
Правильный ответ:
№ 218. Какую часть суток составляют: 1) 3 ч; 2) 8 ч; 3) 12 ч; 4) 16 ч; 5) 21 ч?
Правильный ответ:
№ 219. Какую часть развёрнутого угла составляет угол, градусная мера которого равна: 1) 4°; 2) 12°; 3) 27°; 4) 126°; 5) 153°?
Правильный ответ:
№ 220. Какую часть прямого угла составляет угол, градусная мера которого равна: 1) 2°; 2) 15°; 3) 36°; 4) 75°; 5) 54°.
Правильный ответ:
№ 221. Выполните действие и сократите результат: 1) 7/12 + 3/12; …
Правильный ответ:
№ 222. Выполните действие и сократите результат: 1) 16/63 + 12/63; …
Правильный ответ:
№ 223. Запишите все правильные несократимые дроби со знаменателем 18.
№ 224. Запишите все неправильные несократимые дроби с числителем 20.
№ 225. Сократите:
№ 226. Сократите:
№ 227. Сократите (буквами обозначены натуральные числа):
№ 228. Дробь х/6 сократили на 2 и получили дробь 2/у. Найдите значения х и у.
№ 229. После сокращения дроби 21/а на 3 получили дробь b/4. Найдите значения а и b.
№ 230. Запишите, используя каждую цифру от 0 до 9 только один раз: 1) наименьшее число, кратное 2; 2) наибольшее число, кратное 18.
№ 231. К какому числу надо прибавить 5,7, чтобы произведение полученной суммы и числа 3,6 было равно 120,6?
№ 232. Из какого числа надо вычесть 3,8, чтобы произведение полученной разности и числа 5,5 было равно 34,1?
№ 233. Расположите в порядке возрастания дроби: 9/19, 1/19, 16/19, 5/19, 14/19, 10/19.
№ 234. Сравните:
Конспект урока по математике. Презентация по теме «Сокращение дробей».
Данная методическая разработка презентация разработана по УМК Мерзляк А.Г. 6 класс. Составлена с учётом требований по ФГОС.
Просмотр содержимого документа
«Конспект урока по математике. Презентация по теме «Сокращение дробей».»
Учитель Цыркунова О.А.
На основании чего мы можем умножать числитель и знаменатель дроби?
На основании основного свойства дроби мы можем умножать числитель и знаменатель дроби
Изучение нового материала
Если разделить числитель и знаменатель дроби на наибольший общий делитель , на 12. Какая дробь получится?
На какие числа можно разделить числитель и знаменатель дроби?
При сокращении дроби ее числовое значение не меняете изменилась только ее запись.
— такое преобразование называется сокращением дроби.
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
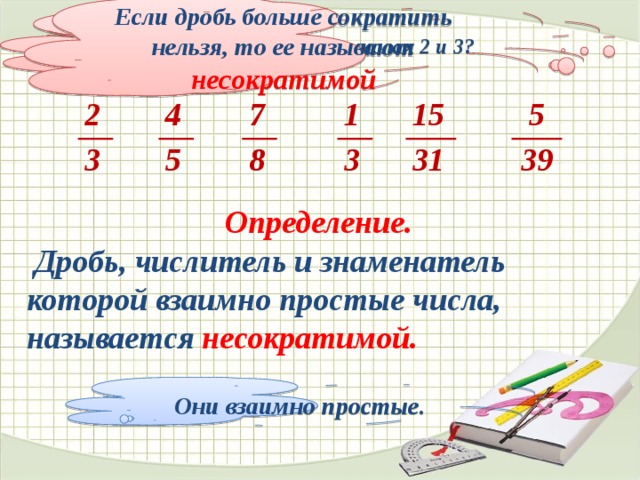
Если дробь больше сократить нельзя, то ее называют несократимой
Что можно сказать о числах 2 и 3?
Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой.
Способы сокращения дробей:
1. Сократить числитель и знаменатель на их НОД.
2. Последовательно сокращать на общие делители.
3. Разложить числитель и знаменатель на множители , а потом сократить.