Что называют содержанием понятия в математике

Особенности математических понятий. Объем и содержание понятия. Определение понятий. Структура определения понятия через род и видовые отличия

Остенсивные определения- это такие определения, вводят понятие путём демонстрации, показаобъектов, которые этим термином обозначаются.

Математика в отличие от других наук изучает окружающий нас мир с особой стороны. Любые математические объекты это результат выделения из предметов и явлений количественных и пространственных св-в и отношений. Т.о. математические объекты реально не существуют. Это идеальные понятия, они существуют лишь в мышлениях человека и в тех знаках и символах, которые образуют математический язык. Более того, при образовании математических понятий кроме абстрагирования им приписывают такие св-ва, которыми не обладает ни один реальный предмет.

Основные матем.понятия: точка, прямая, плоскость, мн-во, число, величина, арифметическое действие.

Любое матем.понятие характеризуется термином, объёмом и содержанием.

Термин – это слово или группа слов, которыми называют элементы некоторого множества. Объём понятия – это мн-во всех объектов, обозначаемых одним и тем же термином. Различают существенные и несущественные св-ва объектов. Св-во будет существенным, если оно присуще объекту, и без него объект не может существовать. Несущественные – отсутствие которых не влияет на существенные объекты.

Содержание понятий – это мн-во всех взаимосвязанных существенных св-в этого понятия или этого объекта.

а-понятие параллелограмм; в-понятие прямоугольник; √вс√а а родовое для в; в-видовое для а; с-понятие четырёхугольник. √а с√с

Одно и то же понятие например параллелограмм может быть родовым для понятия прямоугольник или видовым для понятия четырёхугольник.

Понятия равнобедренный треуг. И прямоугольный треуг. Не находятся в родо-видовых отношениях. Существуют отношения между понятиями как части и целого.

Например, луч это часть прямой, отрезок это часть прямой, дуга это часть окружности.

Если понятия находятся в родо-видовых отношениях, то между объёмом понятия и его содержанием существует такая связь: чем больше объём, тем меньше его содержание и наоборот.

Определение понятий – это логическая операция, раскрывающая содержание понятия. В нём указывают те существенные св-ва, которые достаточны для его распознавания. Определения делятся на явные и неявные (косвенные). Явные определения имеют форму равенства, совпадение двух понятий.

Пример: Параллелограммом наз. четырёхугольник, стороны которого попарно параллельны. а есть в; а- параллелограмм (определяемое понятие; в-четырёхугольник, стороны которого попарно параллельны (определяющее понятие; а=r+v

Определяемое понятие=родовое понятие+видовое отличие

Родо-видовое: Биссектрисой угла наз. луч, выходящий из вершины угла и делящий угол пополам/ r-родовое понятие: луч; v-видовое понятие: выходящий из вершины угла и делящий угол пополам. В начальной школе явное определение через род и видовое отличие применяют редко. Пример: Определение четного числа, прямоугольника, квадрата, умножения.

Явные определения могут иметь и другую структуру: а) генетические определения. Треугольником наз.фигура, состоящая из 3 точек, не лежащих на одной прямой, и 3 отрезков, последовательно их соединяющих.Родовое понятие и способ построения.

б)рекуррентные (рекурсия-возврат) Арифметической прогрессией наз.числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянной для данной последовательности числом d (разность).

В начальной школе преобладают неявные определения. Неявные определения бывают контекстуальные и остенсивные. Контекстуальные определения – в этих определениях содержание новых понятий раскрывается через контекст, анализ конкретной ситуации, описывающей смысл вводимого понятия. Пример: 2+х=5

2. Обучающимся начальных классов предложены задания:

1) Какая фигура лишняя? Ответ объясни.

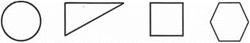2) Какие фигуры можно назвать прямоугольниками? Почему?

• С какой целью можно предложить учащимся эти задания?

• По каким существенным свойствам учащиеся различают фигуры?

• Приведите возможные рассуждения ученика при выполнении каждого задания.

• Опишите методику знакомства учащихся с понятием “прямой угол”.

Источник

Математические понятия

Лекция 5. Математические понятия

1. Объем и содержание понятия. Отношения между понятиями

2. Определение понятий. Определяемые и неопределяемые понятия.

3. Способы определения понятий.

Понятия, которые изучаются в начальном курсе математики, обычно представляют в виде четырех групп. В первую включаются понятия, связанные с числами и операциями над ними: число, сложение, слагаемое, больше и др. Во вторую входят алгебраические понятия: выражение, равенство, уравнения и др. Третью группу составляют геометрические понятия: прямая, отрезок, треугольник и т.д. Четвертую группу образуют понятия, связанные с величинами и их измерением.

Чтобы изучать все разнообразие понятий, надо иметь представление о понятии как логической категории и особенностях математических понятий.

В логике понятиярассматривают как форму мысли, отражающую объекты (предметы и явления) в их существенных и общих свойствах. Языковой формой понятия является слово (термин) или группа слов.

Составить понятие об объекте – это значит уметь отличить его от других сходных с ним объектов. Математические понятия обладают рядом особенностей. Главная заключается в том, что математические объекты, о которых необходимо составить понятие, в реальности не существуют. Математические объекты созданы умом человека. Это идеальные объекты, отражающие реальные предметы или явления. Например, в геометрии изучают форму и размеры предметов, не принимая во внимание другие свойства: цвет, массу, твердость и т.д. От всего этого абстрагируются. Поэтому в геометрии вместо слова «предмет» говорят «геометрическая фигура».

Результатом абстрагирования являются и такие математические понятия, как «число» и «величина».

Вообще математические объекты существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык.

К сказанному можно добавить, что, изучая пространственные формы и количественные отношения материального мира, математика не только пользуется различными приемами абстрагирования, но и само абстрагирование выступает как многоступенчатый процесс. В математике рассматривают не только понятия, появившиеся при изучении реальных предметов, но и понятия, возникшие на основе первых. Например, общее понятие функции как соответствия является обобщением понятий конкретных функции, т.е. абстракцией от абстракций.

Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали. Можно указать и другие его свойства.

Среди свойств объекта различают существенные и несущественные. Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать. Например, для квадрата существенными являются все свойства, названные выше. Несущественно для квадрата АВСD свойство «сторона АВ горизонтальна».

Когда говорят о математическом понятии, то обычно имеют в виду множество объектов, обозначаемых одним термином(словом или группой слов). Так, говоря о квадрате, имеют в виду все геометрические фигуры, являющиеся квадратами. Считают, что множество всех квадратов составляет объем понятия «квадрат».

Вообще, объем понятия – это множество всех объектов, обозначаемых одним термином.

Любое понятие имеет не только объем, но и содержание.

Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии.

Рассмотрим, например, понятие «прямоугольник».

Объем понятия – это множество различных прямоугольников, а в его содержание входят такие свойства прямоугольников, как «иметь четыре прямых угла», «иметь равные противоположные стороны», «иметь равные диагонали» и т.д.

Между объемом понятия и его содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Так, например, объем понятия «квадрат» является частью объема понятия «прямоугольник», а в содержании понятия «квадрат» содержится больше свойств, чем в содержании понятия «прямоугольник» («все стороны равны», «диагонали взаимно перпендикулярны» и др.).

Любое понятие нельзя усвоить, не осознав его взаимосвязи с другими понятиями. Поэтому важно знать, в каких отношениях могут находиться понятия, и уметь устанавливать эти связи.

Отношения между понятиями тесно связаны с отношениями между их объемами, т.е. множествами.

Условимся понятия обозначать строчными буквами латинского алфавита: а, b, c, d, …, z.

Пусть заданы два понятия а и b. Объемы их обозначим соответственно А и В.

Если А ⊂ В (А ≠ В), то говорят, что понятие а – видовое по отношению к понятию b, а понятие b – родовое по отношению к понятию а.

Если А = В, то говорят, что понятия А и В тождественны.

Например, тождественны понятия «равносторонний треугольник» и «равнобедренный треугольник», так как их объемы совпадают.

Рассмотрим подробнее отношение рода и вида между понятиями.

2. Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник». Среди указанных можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм».

3. В-третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.

Так как объем понятия – множество, удобно, устанавливая отношения между объемами понятий, изображать их при помощи кругов Эйлера.

Установим, например, отношения между следующими парами понятий а и b, если:

1) а – «прямоугольник», b – «ромб»;

2) а – «многоугольник», b – «параллелограмм»;

3) а – «прямая», b – «отрезок».

Отношения между множествами отображены на рисунке соответственно

2. Определение понятий. Определяемые и неопределяемые понятия.

Появление в математике новых понятий, а значит, и новых терминов, обозначающих эти понятия, предполагает их определение.

Определениемобычно называют предложение, разъясняющее суть нового термина (или обозначения). Как правило, делают это на основе ранее введенных понятий. Например, прямоугольник можно определить так: «Прямоугольником называется четырехугольник, у которого все углы прямые». В этом определении есть две части – определяемое понятие (прямоугольник) и определяющее понятие (четырехугольник, у которого все углы прямые). Если обозначить через а первое понятие, а через b – второе, то данное определение можно представить в таком виде:

а есть (по определению) b.

Слова «есть (по определению)» обычно заменяют символом ⇔, и тогда определение выглядит так:

Читают: «а равносильно b по определению». Можно прочитать эту запись еще и так: «а тогда и только тогда, когда b.

Определения, имеющие такую структуру, называются явными. Рассмотрим их подробнее.

Обратимся ко второй части определения «прямоугольник».

В нем можно выделить:

1) понятие «четырехугольник», которое является родовым по отношению к понятию «прямоугольник».

2) свойство «иметь все углы прямые», которое позволяет выделить из всевозможных четырехугольников один вид – прямоугольники; поэтому его называют видовым отличием.

Вообще видовое отличие – это свойства (одно или несколько), которые позволяют выделить определяемые объекты из объема родового понятия.

Итоги нашего анализа можно представить в виде схемы:

Знак «+» используется как замена частица «и».

Нам известно, что любое понятие имеет объем. Если понятие а определено через род и видовое отличие, то о его объеме – множестве А – можно сказать, что в нем содержатся такие объекты, которые принадлежат множеству С (объему родового понятия с) и обладают свойством Р:

Так как определение понятия через род и видовое отличие является по существу условным соглашением о введении нового термина для замены какой-либо совокупности известных терминов, то об определении нельзя сказать, верное оно или неверное; его не доказывают и не опровергают. Но, формулируя определения, придерживаются ряда правил. Назовем их.

1. Определение должно быть соразмерным. Это означает, что объемы определяемого и определяющего понятий должны совпадать.

2. В определении (или их системе) не должно быть порочного круга. Это означает, что нельзя определять понятие через само себя.

3. Определение должно быть ясным. Требуется, например, чтобы значения терминов, входящих в определяющее понятие, были известны к моменту введения определения нового понятия.

4. Одно и то же понятие определить через род и видовое отличие, соблюдая сформулированные выше правила, можно по-разному. Так, квадрат можно определить как:

а) прямоугольник, у которого соседние стороны равны;

б) прямоугольник, у которого диагонали взаимно перпендикулярны;

в) ромб, у которого есть прямой угол;

г) параллелограмм, у которого все стороны равны, а углы прямые.

Различные определения одного и того же понятия возможны потому, что из большого числа свойств, входящих в содержание понятия, в определение включаются только некоторые. И тогда из возможных определений выбирают одно, исходят из того, какое из них проще и целесообразнее для дальнейшего построения теории.

Назовем ту последовательность действий, которую мы должны соблюдать, если хотим воспроизвести определение знакомого понятия или построить определение нового:

1. Назвать определяемое понятие (термин).

2. Указать ближайшее родовое понятие (по отношению к определяемому) понятие.

3. Перечислить свойства, выделяющие определяемые объекты из объема родового, т.е сформулировать видовое отличие.

4. Проверить, выполнены ли правила определения понятия (соразмерно ли оно, нет ли порочного круга и т.д.).

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Конспект урока по ТОНКМ с МП по теме «Математические понятия. Объем и содержание математических понятий»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Тема: Основные математические понятия. Объем и содержание понятий

Цель: добиться осознанного усвоения студентами понятий «существенные и несущественные свойства объекта», «объём и содержание математического понятия»; начать процесс формирования умения выделять объём и содержание математического понятия.

Познакомиться с основными видами математических понятий, учиться выделять существенные и несущественные свойства объекта, объем и содержание математических понятий;

Развивать математическую речь, мышление, анализ, синтез, обобщение, классификацию;

Воспитывать познавательный интерес, коммуникативную культуру

Оборудование: учебные пособия по ТОНКМ (Л.П. Стойлова, А.М. Пышкало), математике (Л.П. Стойлова); раздаточный материал.

I . Организационный момент.

III . Открытие нового знания

Математика, как и другие науки, изучает окружающий нас мир, природные и общественные явления, но изучает лишь их особые стороны (например, в геометрии изучают форму и размеры предметов, не принимая во внимание другие их свойства: цвет, массу, твердость и т. д. От всего этого отвлекаются, абстрагируются).

Любые математические объекты ­– это результат выделения из предметов и явлений окружающего мира количественных и пространственных свойств и отношений и абстрагирования их от всех других свойств. Следовательно, математические объекты реально не существуют, нет в окружающем нас мире геометрических фигур, чисел и т. д. Все они созданы человеческим умом в процессе исторического развития общества и существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык.

Более того, при образовании математических объектов происходит не только абстрагирование от многих свойств соответствующих предметов, но и приписывание им таких свойств, которыми никакие реальные предметы не обладают (например, в таком математическом объекте, как прямая, отражено не только свойство протяженности реальных предметов, но и свойство неограниченной протяженности в обоих направлениях, хотя никакой из реально существующих предметов таким свойством не обладает).

Вообще абстрактность математики позволяет применять ее в самых разных областях знания, поскольку она представляет собой могущественный инструмент познания природы и создания техники.

Понятия, которые изучаются в НКМ, обычно представляют в виде 4 групп:

Понятия, связанные с числами и операциями над ними: число, сложение, слагаемое, больше и т.д.

Алгебраические понятия: выражение, равенство, уравнение и т.д.

Геометрические понятия: прямая, отрезок, треугольник, пирамида и т.д.

Понятия, связанные с величинами и их измерением: время, километр, площадь и т.д.

такие свойства, отсутствие которых не влияет на существование объекта.

Пример. ABCD – квадрат (рис. 1).

Существенные свойства : четыре стороны; четыре прямых угла; все стороны равны; диагонали равны; диагонали пересекаются под прямым углом и др.

Несущественное свойство : сторона ВС – горизонтальная (если квадрат АВС D повернуть (рис. 1), то сторона ВС окажется расположенной по-другому).

– Назовите какие-нибудь существенные и несущественные свойства треугольника.

Совокупность всех взаимосвязанных существенных свойств объекта называют содержанием понятия об этом объекте.

Объем понятия — это совокупность всех объектов, обозначаемых одним и тем же термином.

Объём понятия «квадрат»

– Что входит в объём понятия «треугольник»?

Между объемом понятия и его содержанием существует связь: чем «больше» объем понятия, тем «меньше» его содержание, и наоборот, чем «меньше» объём понятия, тем «больше» его содержание (например, объем понятия «прямоугольный треугольник» «меньше» объема понятия «треугольник», поскольку в объем первого понятия входят не все треугольники, а только прямоугольные. Но содержание первого понятия «больше» содержания второго: прямоугольный треугольник обладает не только всеми свойствами треугольника, но и другими, присущими только прямоугольным треугольникам).

– Сравните объём и содержание понятий «четырёхугольник» и «прямоугольник»

III . Первичное закрепление изученного материала

Выделите объем и содержание следующих понятий:

V . Подведение итогов урока

– Как вы понимаете слова Дж. Гиббса «Математика – это язык природы»?

– Назовите существенные свойства ромба.

– Что входит в объём понятия «треугольник»?

V . Домашнее задание (с инструктажем)

Источник

Лекция 6. Объем и содержание понятия. Отношения между понятиями.

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Лекция 4. Объем и содержание понятия. Отношения между понятиями.

Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла и др. Различают свойства существенные и несущественные.

Для квадрата: АВСД существенные свойства: АВ = ВС = СД =ДА,

Если квадрат повернуть, сохранятся только существенные свойства, именно они и составляют понятие об объекте.

Рассмотрим пример для дошкольников, используя наглядный материал

— Маленький черный треугольник.

— Большой белый треугольник.

— Чем фигуры отличаются?

— Что есть у треугольника?

Совокупность всех существеннных свойств объекта называют содержанием понятия.

Совокупность всех объектов, обозначаемая одним термином, составляет объем понятия.

Итак, любое понятие характеризуется:

— объемом (совокупность всех объектов, называемых этим термином);

— содержанием (совокупность всех существенных свойств объектов, входящих в объем понятия).

Между объемом понятия и его содержанием существует связь: чем «больше» объем понятия, тем «меньше» его содержание, и наоборот. Объем понятия «треугольник» «больше», чем объем понятия «прямоугольный треугольник», так как все объекты второго понятия являются и объектами первого понятия. Содержание понятия «треугольник» «меньше», чем содержание понятия «прямоугольный треугольник», так как прямоугольный треугольник обладает всеми свойствами любого треугольника и еще другими свойствами, присущими только ему.

Для распознавания объекта необязательно проверять у него все существенные свойства, достаточно лишь некоторых. Этим пользуются, когда понятию дают определение.

Определение понятия – это логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина. Определение понятия позволяет отличать определяемые объекты от других объектов. Так, например, определение понятия «прямоугольный треугольник» позволяет отличить его от других треугольников.

Различают явные и неявные определения. Явные определения имеют форму равенства двух понятий. Одно из них называют определяемым другое определяющим.

Следует иметь в виду, что понятия рода и вида относительны. Так, «прямоугольник» – это родовое к понятию «квадрат», но видовое по отношению к понятию «четырехугольник».

Кроме того, для одного понятия могут существовать несколько родовых. Например, для квадрата родовыми являются ромб, четырехугольник, многоугольник, геометрическая фигура. В определении через род и видовое отличие для определяемого понятия принято называть ближайшее родовое понятие.

Таким образом, определение через род и видовое отличие имеет следующую структуру:

Определяемое = Род + Видовое

Задания для самостоятельной работы по теме:

1. Каков объем понятий: «цифра», «автомобиль», «снегурочка», «волк», «столица России», «двузначное число».

2. Решите анаграммы. Исключите лишнее слово. Ответ обоснуйте:

Источник