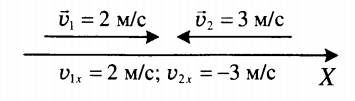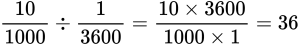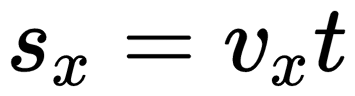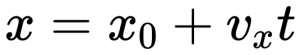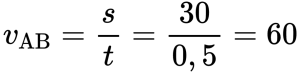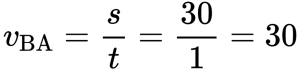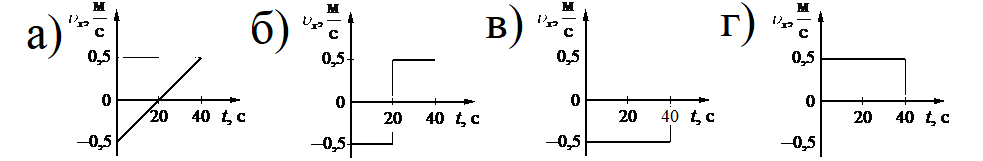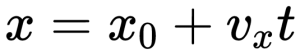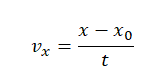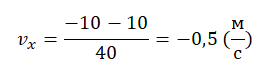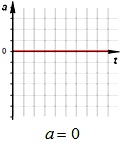Что называют скоростью равномерного прямолинейного движения какая формула выражает

Кинематика. Равномерное движение.

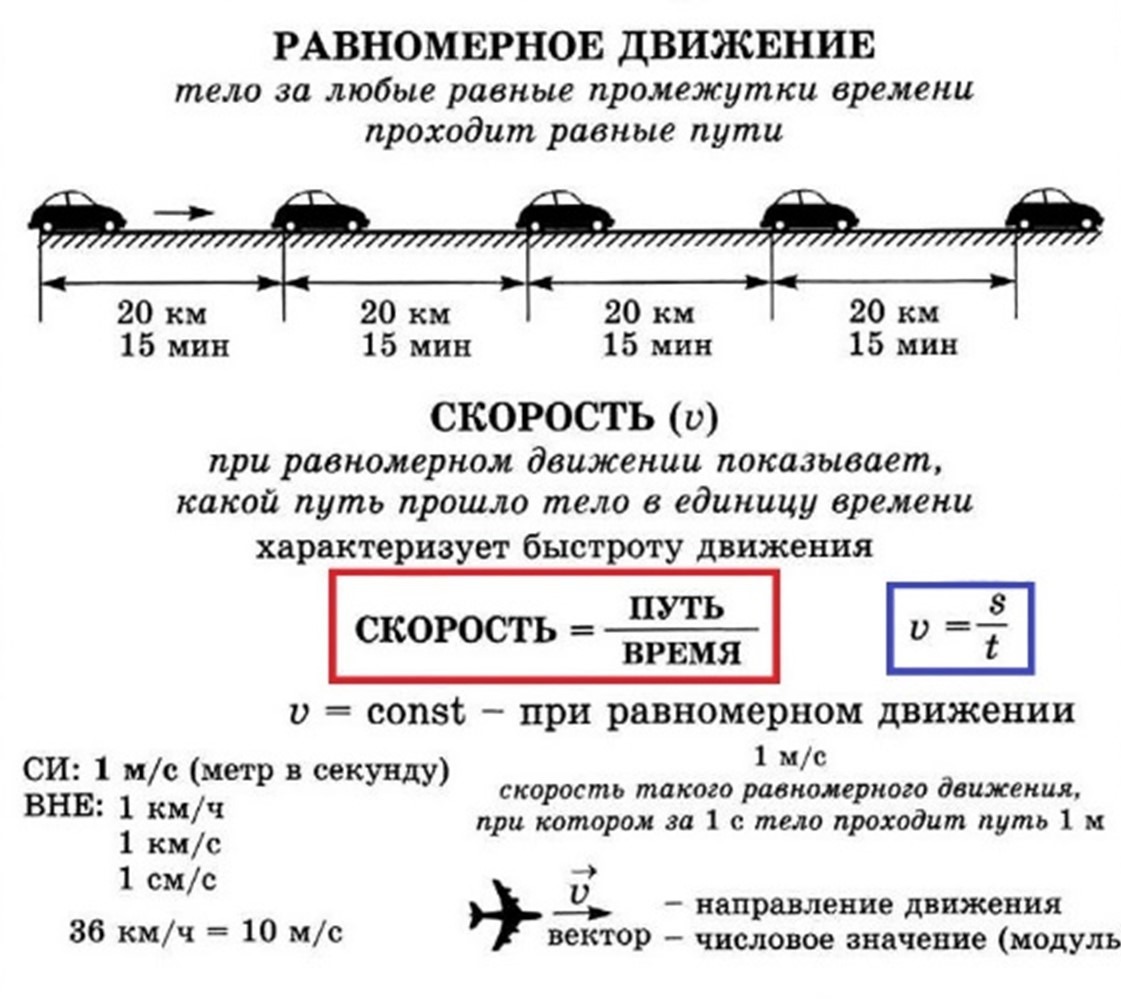
Если тело за любые равные промежутки времени проходит равные пути, его движение называется равномерным.

Равномерное движение встречается довольно редко. Например, почти равномерно движется Земля вокруг Солнца, проходя за год один оборот.

При равномерноем движении скорость не изменяется:

Равномерное движение происходит как по прямолинейной, так и по криволинейной траектории.

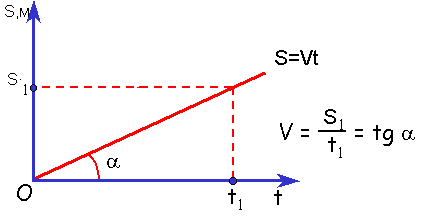
Равномерное движение тела описывается уравнением:

где s – путь, пройденный телом от некоторой точки, принятой за начало отсчета, t – время тела в пути, s₀ – значение s в начальный момент времени t = 0.

Прямолинейным равномерным движением называют движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Скорость прямолинейного равномерного движения – величина постоянная. Определяется как отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло:

Модуль этой скорости – это перемещение тела, совершаемое за единицу времени.

Скоростью равномерного прямолинейного движении называют величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка:

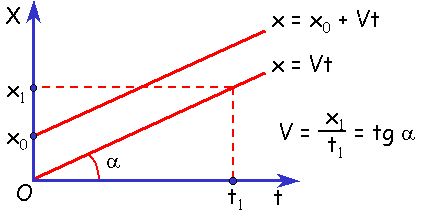
Перемещение при равномерном прямолинейном движении (по оси Х) можно рассчитать по формуле:

где υ_x – проекция скорости на ось Х, откуда закон равномерного прямолинейного движения будет иметь вид:

Источник

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

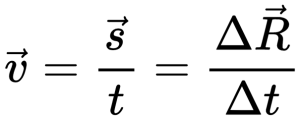
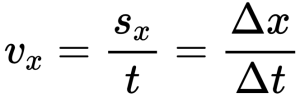
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Спидометр — прибор для измерения модули скорости тела.

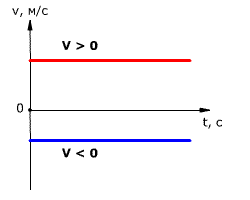
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

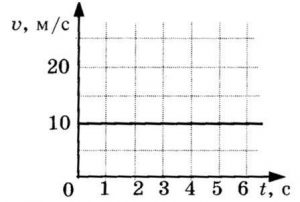
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

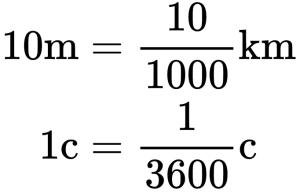
Перемещение и координаты тела при равномерном прямолинейном движении

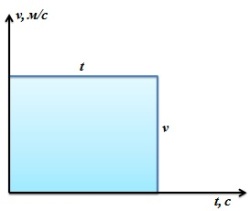
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

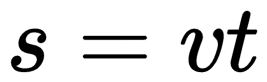
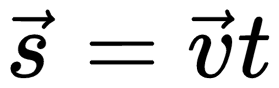
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

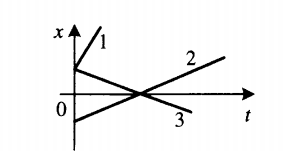
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид :

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

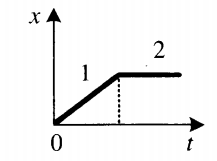
Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

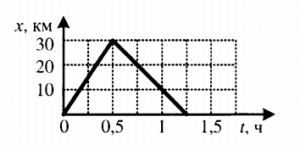
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Алгоритм решения

Уравнение координаты при равномерном прямолинейном движении имеет вид:

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Какое движение называют равномерным прямолинейным

Равномерное прямолинейное движение — что это в физике

Прежде чем перейти непосредственно к изучению понятия равномерного прямолинейного движения, необходимо рассмотреть его составляющие.

Прямолинейное движение — движение по прямой линии.

Равномерное движение — механическое движение, при котором материальная точка за одинаковые отрезки времени проходит одинаковые расстояния. Величина скорости v остается постоянной и неизменной.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Равномерное движение практически невозможно в обычной жизни, поскольку для этого необходимы очень специфичные обстоятельства. На движущееся тело воздействует множество сил: тяжести, реакции опоры, трения, сила, под воздействием которой двигается тело. Чтобы тело двигалось равномерно, необходимо, чтобы эти силы были уравновешены определенным образом.

Также стоит учитывать особенность величины скорости, которая заключается в том, что скорость относительна и зависит от системы отсчета. Так, если человек движется в поезде, его скорость относительно поезда будет одной, а относительно статичных объектов вне поезда — другой.

Исходя из предыдущих определений и их отличительных признаков, можно вывести искомое.

Равномерное прямолинейное движение — это движение по прямой, при котором тело за любые равные промежутки времени проходит одинаковые расстояния.

Скорость такого движения постоянна и не зависит от времени. Ее вектор совпадает с вектором перемещения в каждой точке траектории.

Как записывается кинематический закон прямолинейного равномерного движения

Основная задача механики заключается в том, чтобы указать положение тела в пространстве в любой момент времени. Это помогает предсказать положение тела не только в настоящем, но и в любой момент в будущем. Выполнять эту цель помогает закон движения.

Закон движения — это математическая формулировка, описывающая, как двигается тело. Это набор зависимостей, которые выявляют данные о движении материальной точки.

При равномерном прямолинейном движении тела по оси Ox за время t уравнение предстает в виде:

Это уравнение следует из двух уравнений:

Скорость при прямолинейном равномерном движении

Скорость движения (v) — это величина, которая равна отношению перемещения тела за некоторый промежуток времени к этому промежутку.

Т. е. скорость движения тела показывает, какое перемещение совершает тело за единицу времени. Чем больше перемещение за определенный отрезок времени, тем больше скорость.

При прямолинейном равномерном движении скорость остается постоянной по модулю и направлению. Ускорение равно нулю.

В СИ главной единицей измерения скорости является 1 метр в секунду.

Сокращенно эту единицу обозначают как 1 м/с. Иногда используют дополнительные единицы:

Для измерения модуля скорости используют прибор спидометр.

Основные формулы

Перемещение является векторной величиной.

Скорость тоже является векторной величиной. Это значит, что она имеет не только модуль, но и направление.

При этом время не имеет направления, т. е. является скалярной величиной.

Исходя из определения, скорость равна перемещению, деленному на время, за которое это перемещение состоялось.

Запишем формулу в векторном виде:

Если направления скорости и перемещения не имеют значения для решения задачи, векторы можно не учитывать. Тогда вычисления со скоростью и перемещением производятся как с обычными скалярными величинами.

Выведем дополнительные формулы.

Векторное перемещение, или же скалярный пройденный при движении путь, равен скорости, умноженной на время.

\(\overrightarrow s=\overrightarrow v\cdot t \ или \overrightarrow s=\overrightarrow v\cdot t\;или\;s=v\cdot t\;\)

Тогда время, за которое тело со скоростью v переместилось на расстояние s, равно:

Примеры равномерного прямолинейного движения

Равномерное прямолинейное движение в жизни почти не встречается. Это идеализация, которая использует характеристики прямолинейного движения для упрощения расчета. Создать такие условия, чтобы тело могло достаточно долго двигаться с одинаковой скоростью, почти невозможно. Но движения в реальном, а не идеальном мире могут быть приближены к равномерному с некой степенью погрешности.

Ближе всего в природе к равномерному движению находится движение небесных тел в космосе, где они слабо взаимодействуют друг с другом, а воздействием других сил можно пренебречь.

Есть и другие примеры движения, которое близко к прямолинейному равномерному:

Решение задач

Учащийся автошколы тренируется водить автомобиль. Инструктор дает ему задание ехать по прямой дороге до поворота 3 км и держать при этом скорость 60 км/ч. Сколько времени понадобится водителю, чтобы доехать до поворота?

Вспомним формулу нахождения скорости при равномерном прямолинейном движении.

Выведем из нее формулу нахождения времени:

Ответ можно было бы записать в таком виде, но лучше привести их к единицам СИ, т. е. к секундам.

Спортсмен решил проверить свою выносливость и попросил работников аэропорта дать ему пробежаться по взлетной полосе с неизменной скоростью. Когда он пробегал мимо друга на 7 метре взлетной полосы, его друг секундомером засек время и определил скорость спортсмена. Она оказалась равна 18 км/ч. На каком метре взлетной полосы окажется спортсмен через 3 секунды?

Запишем уравнение равномерного прямолинейного движения:

Производить вычисления пока нельзя, т. к. единицы измерения величин различны. Переведем км/ч в м/с: \(18\;км/ч\;=\;\frac<18\cdot1000><3600>=5\;м/с \)

Источник

Как сказал.

Стремись не к тому, чтобы добиться успеха, а к тому, чтобы твоя жизнь имела смысл.

Альберт Эйнштейн

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Равномерное прямолинейное движение

Равномерным прямолинейным движением называют движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Прямолинейное движение — это движение, при котором траектория прямая. То есть это движение тела по прямой линии.

Скорость равномерного прямолинейного движения — это физическая векторная величина, равная отношению перемещения тела S за любой промежуток времен к значению этого промежутка t:

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор скорости совпадает с вектором перемещения.

Из данной формулы. мы легко можем выразить перемещение тела при равномерном движении:

Уравнение координаты тела:

Рассмотрим зависимость скорости и перемещения от времени

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

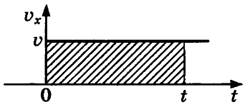
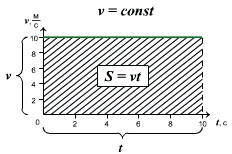
Проекция перемещения тела численно равна площади прямоугольника под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения перемещения (пути) по графику v(t) : при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол a, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t) и x(t) : Тангенс угла наклона графика к оси времени равен скорости движения.

х₀ — начальная координата движущегося тела

v_ср — средняя скорость равномерного прямолинейного движения

v_х — скорость равномерного прямолинейного движения

S — перемещение тела (расстояние, на которое передвинулось тело)

t — промежуток времени перемещения (время)

a — угол наклона графика к оси времени

Источник

Равномерное движение

Школьный курс физики содержит раздел «кинематика». Большинство задач этого раздела можно решить, рассматривая движение вдоль одной оси — одномерное движение. Его еще называют прямолинейным движением.

Для некоторых задач нужно рассматривать движение на плоскости – двумерный случай.

Вообще, движение тела может происходить:

Здесь рассмотрим одномерный случай движения — движение тел вдоль оси.

Параметры, описывающие движение

Чтобы описать движение, используют:

Траектория – линия, вдоль которой двигалось тело.

Траектория – скаляр, в СИ длину траектории измеряют в метрах.
Для криволинейного движения траектория будет отрезком кривой.
Если движение прямолинейное, траектория – отрезок прямой линии.

Перемещение тела – это вектор. Он соединяет точки, в которых тело находилось в начале и конце движения, направлен из начальной точки в конечную.
Модуль этого вектора – его длину, в СИ измеряют в метрах.

Может ли перемещение тела равняться нулю, при том, что траектория имеет какую-либо протяженность?
Да, такое может быть. Когда тело движется так, что в конце движения оно вернется в начальную точку, в которой находилось перед началом движения.
Если в завершении движения тело окажется на каком-то расстоянии от начальной точки, длина вектора перемещения будет положительной.

Примечания:

Уравнение движения — описывает характер движения.

Вместо координат тела уравнение движения может содержать перемещение.

Примечания:

Описанные параметры применяют и для равномерного и для неравномерного движения.

Прямолинейное движение вдоль оси

Рассмотрим движение по прямой, когда скорость тела не меняется. Это — равномерное прямолинейное движение.

На рисунке 1 представлено движение тела вдоль оси, назовем ее для определенности Ox:

Ось «Ox» на рисунке 1 обозначена большим символом «X».
Точка, в которой тело находилось в начале движения \(x_ <0>\left( \text <м>\right)\) — начальная координата тела;
В эту точку тело переместилось к концу движения \(x \left( \text <м>\right)\) — конечная координата тела;
Расстояние между двумя точками \(S \left( \text <м>\right)\) – это перемещение тела. Перемещение – это вектор.

Формула перемещения для одномерного случая

Для движения по оси (одномерный случай), длину перемещения находят так:
\[ \large \boxed < S = \left| x — x_<0>\right| >\]
Знак модуля нужен для того, чтобы длина перемещения оставалась положительной, даже, если движение происходит влево по оси, т. е. против направления оси Ox.
Сравним два случая движения тел. Первый – в положительном направлении оси Ox (рис 2а), второй – в направлении, противоположном оси (рис 2б).

Чтобы найти длину вектора перемещения при движении в положительном направлении оси (рис. 2а), модуль раскрываем так:
\[ S = \left| x — x_ <0>\right| = x — x_ <0>\]
Для движения в отрицательном направлении оси (рис. 2б), длина вектора перемещения выражается так:
\[ S = \left| x — x_ <0>\right| = — \left( x — x_ <0>\right) = x_ <0>— x \]
И в первом, и во втором случае, длина (модуль) вектора перемещения окажется положительной.

Скорость равномерного движения

В учебниках физики равномерному движению дают такое определение:
Движение равномерное, когда тело за одинаковые интервалы времени проходит равные расстояния.

Упростим формулировку:
Если каждую секунду тело проходит одинаковые расстояния – оно движется равномерно.

Слово «равномерное» состоит из двух частей.
Если разбить его на части, получим
«равно» — одинаковый, равный,
«мерное» — отмерять.
Или, другими словами: каждую секунду отмеряем одинаковые расстояния (рис. 2).

Для равномерного движения тела его

\[ \left|\vec \right| = \left|\vec \right|\cdot t \]

Эта формула называется уравнением движения. Или, развернуто: «уравнение равномерного прямолинейного движения».

Где \( \left|\vec \right| \) — длина (модуль) вектора перемещения и, \(\left|\vec \right|\) — длина (модуль) вектора скорости.

Уравнение движения можно записать проще:

\(S \left( \text <м>\right)\) – расстояние, пройденное телом (перемещение).

\(t \left( c \right)\) – промежуток времени, в течение которого тело двигалось.

\(v \left( \frac<\text<м>> \right)\) – скорость, с которой двигалось тело.

Разделив обе части уравнения \( S = v \cdot t \) на интервал времени \( t \), получим выражение для скорости тела:

График уравнения равномерного движения

Вспомним, что перемещение является разностью конечных и начальных координат тела

\( S = \left| x — x_ <0>\right| \)

Воспользуемся тем, что при движении вдоль положительного направления оси модуль можно раскрыть так:

\( \left| x — x_ <0>\right| = x — x_ <0>\)

Тогда уравнение движения перепишем так:

\[ \large \boxed < x — x_<0>= v \cdot t >\]

Прибавим к обеим частям уравнения величину \( x_ <0>\). Получим такую запись

\[ \large x = v \cdot t + x_<0>\]

Это уравнение задает на плоскости tOx линию. Ее график на осях «x» и «t» — это прямая линия.

Вспомним, что для прямой линии в математике применяют такой вид записи:

Сравним два уравнения:

\[ \begin x = v\cdot t + x_<0>\\ y = k\cdot x + b \end \]

Видно, что число \( x_<0>\) – начальная координата тела, выполняет роль коэффициента \(b\).

А скорость тела \( v\) – играет роль углового коэффициента \(k\).

Сравним графики линий (рис. 4), описанных соотношениями \( y = k \cdot x + b\) и \( x = v \cdot t + x_<0>\)

Видно, что линия на рисунке 4а, располагается и слева и справа от вертикальной оси.

Линия же, описывающая движение тела, представленная на рисунке 4б, располагается только лишь в правой полуплоскости. Это не с проста. На горизонтальной оси рисунка 4б отложено время, а в левой полуплоскости время будет отрицательным. При решении задач физики мы считаем, что в начальный момент задачи время равно нулю. Поэтому, область отрицательного времени в физике нас не интересует.

Рассмотрим теперь на графике равномерное движение двух тел, обладающих разными скоростями (рис. 5). Движение тела 1 на рисунке описывает синяя линия, а тела 2 – красная.

Два тела стартуют из точки \( x_<0>\) и двигаются равномерно воль оси Ox. За промежуток времени \( \Delta t\) тело 1, проходит больший путь, чем тело 2.

Примечание: Чем сильнее на графике x(t) прямая линия прижимается к вертикали, тем больше скорость, с которой движется тело!

Как отмечалось выше, тело может двигаться не только в положительном направлении вдоль оси, но и в отрицательном направлении.

На следующем рисунке представлены случаи движения тела в положительном (рис. 6а) и, в отрицательном (рис. 6б) направлениях оси Ox.

Когда скорость направлена по оси (рис. 6а) — координата «x» увеличивается,

а когда против оси (рис. 6б) — координата «x» уменьшается.

На рисунке рядом с прямыми x(t) приведены уравнения движения. Когда скорость направлена против оси (рис. 6б), перед ней записывают знак «минус».

Угол \(\alpha\) на рисунке связан со знаком скорости. Если скорость направлена по оси (рис. 6а), то угол будет острым. А если скорость направлена против оси (рис. 6б) – угол тупой.

Примечание: Скорость – это вектор. Когда вектор направлен против оси, его проекция на эту ось будет отрицательной. Читайте тут о проекциях векторов. Длина любого вектора – это положительная величина.

Как по графику перемещения определить скорость

Пользуясь графиком функций S(t), или x(t) равномерного движения можно определить скорость, с которой движется тело.

Примечания:

Скорость находим за четыре шага (рис. 7):

Полученное число и будет скоростью тела.

Примечания:

Обращаем внимание на то, в каких единицах на осях измерены расстояние S и время t. Если нужно, переводим расстояние в метры, а время — в секунды, чтобы получить скорость в правильных единицах измерения.

Рассмотрим рисунок 7.

На рисунке первая точка имеет координаты \( \left( t_ <1>; x_ <1>\right) \),

координаты второй точки: \( \left( t_ <2>; x_ <2>\right) \).

Разницы между координатами находим, руководствуясь принципом («конечная» — «начальная») по формулам

Скорость вычислим из соотношения

Читайте далее о том, как переводить скорость из километров в час в метры в секунду и о равнопеременном движении

Источник