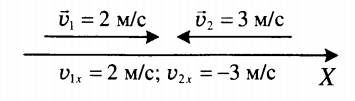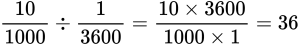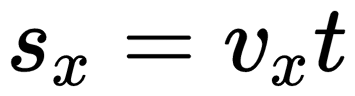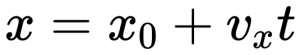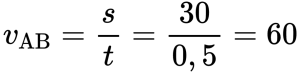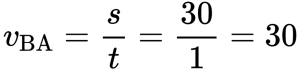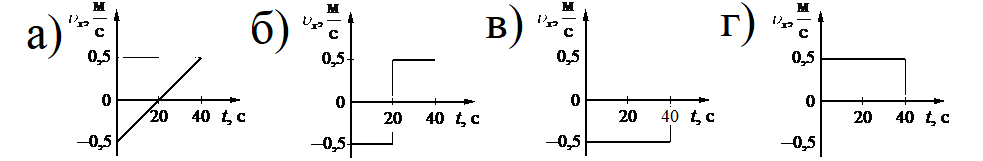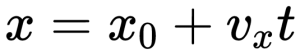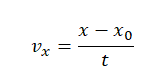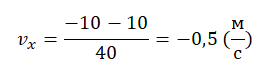Что называют скоростью при равномерном прямолинейном движении
Равномерное прямолинейное движение
теория по физике 🧲 кинематика
Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.
Скорость при прямолинейном равномерном движении
Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.
Векторный способ записи скорости при равномерном прямолинейном движении: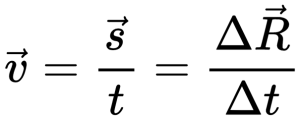
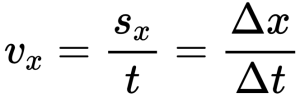
s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: 
sx — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат: 
Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.
Спидометр — прибор для измерения модули скорости тела.
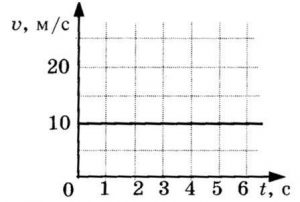
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:
Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.
График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:
Теперь нужно разделить километры на часы: 
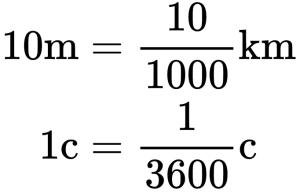
Перемещение и координаты тела при равномерном прямолинейном движении
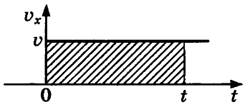
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.
При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:
Вектор перемещения равен произведению вектора скорости на время движения: 
Внимание!
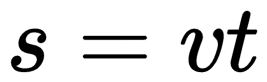
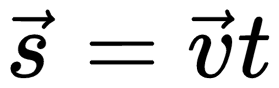
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.
Формула проекции перемещения:
График проекции перемещения
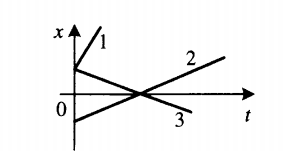
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси sx.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси sx меньше.
График координаты
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:
Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид :
Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.
Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.
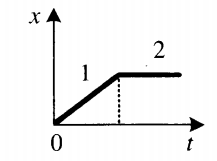
Пример №2. График зависимости координаты тела от времени имеет вид: 
Изучите график и на его основании выберите два верных утверждения:
На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.
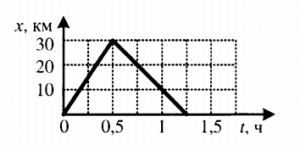
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?
Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:
Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:
Скорость во время движения от В к А равна:
Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.
Алгоритм решения
Уравнение координаты при равномерном прямолинейном движении имеет вид:
Отсюда проекция скорости равна:
Начальная координата xo = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.
Вычисляем проекцию скорости:
Этому значению соответствует график «в».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Весь график можно поделить на 3 участка:
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить