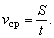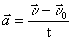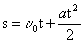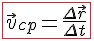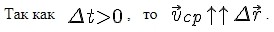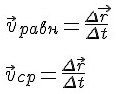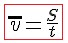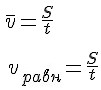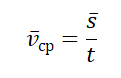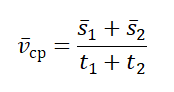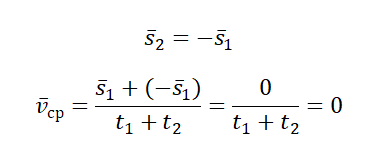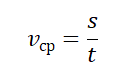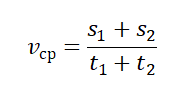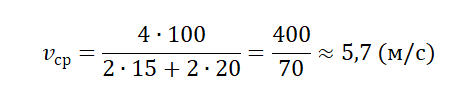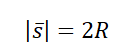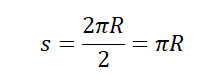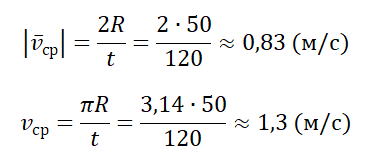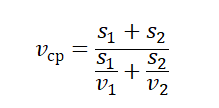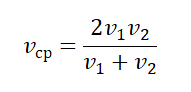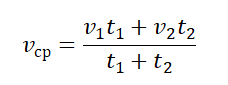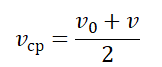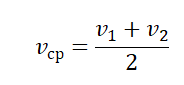Что называют скоростью переменного движения

то средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь:

Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, называется ускорение.

Мгновенное ускорение 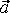_мгн – это вектор ускорения материальной точки в любой момент времени.

Равномерно-переменное движение — это движение, при котором за одинаковые промежутки времени скорость увеличивается или уменьшается на одинаковую величину.

Скорость равномерно-переменного движения выражается формулой v = v₀ + at, (19)

где v—скорость равномерно-переменного движения в данный момент, м/сек;

Ускорением называется изменение скорости в единицу времени.

Ускорение а имеет размерность скорость / время = м / сек 2 и выражается формулой a = (v-v₀)/t. (20)

Путь, пройденный при равномерно-переменном движении, выражается формулой S= ((v₀+v)/2)* t = v₀t+(at 2 )/2. (21)

авномерное движение точки по окружности— движение точки с постоянной по модулю скоростью (v=const) по траектории, представляющей собой окружность. Но, т.к. скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит равномерное движение по окружности – ускоренное движение! Точка совершает перемещение с постоянной по модулю скоростью, следовательно: .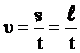

мВремя, за которое тело совершает один оборот, т.е. поворачивается на угол 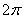, называется периодом обращения

Частотой обращения называется число оборотов по окружности в единицу времени.

Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:

Источник

Что называют скоростью переменного движения

§ 17. Переменное движение. Средняя скорость. Средний модуль скорости

1. Переменное движение.

2. Средняя скорость.

Определение 2а. Средней скоростью переменного движения называется отношение перемещения ко времени, за которое это перемещение произошло.

Запишем формулу скорости равномерного движения и средней скорости переменного движения.

Если посмотреть на правые части этих равенств, заметим, что они одинаковы. В этом заключается смысл средней скорости.

Определение 2б. Под средней скоростью переменного движения понимают скорость некоторого воображаемого равномерного прямолинейного движения, у которого перемещение и время одинаковы с переменным движением.

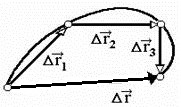
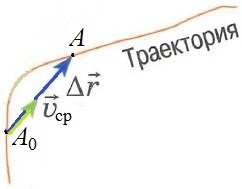
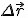
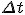
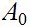
Согласно рисунку, представленному выше, это понимать надо так. Если бы точка двигалась не переменно по криволинейной траектории, а равномерно и прямолинейно прямо по вектору перемещения , то она за время попала бы в точку A из точки , если бы скорость этого воображаемого равномерного движения была бы одинаковой со средней скоростью переменного движения.

Модуль вектора средней скорости, или модуль средней скорости :

.

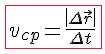
3. Средний модуль скорости.

На практике при составлении расписания движения поездов, автобусов используют ещё одно понятие средней скорости, которое называют средним модулем скорости, то есть средним по времени модулем всех скоростей, которые имела точка на различных участках траектории.

Определение 3а. Средним модулем скорости переменного движения называется отношение пути S ко времени t, за которое этот путь пройден.

— средний модуль скорости

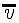
Не надо путать средний модуль скорости с модулем вектора средней скорости.

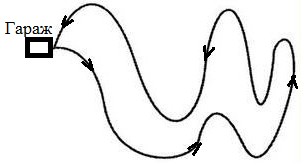
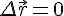
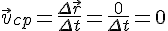
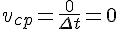
Например, если автобус вышел на маршрут в начале дня и к концу дня возвратился в гараж, то перемещение за всё время движения равно нулю . Поэтому равны нулю средняя скорость и её модуль:

, .

Но средний модуль скорости отличен от нуля, так как не равен нулю путь, пройденный автобусом:

.

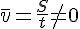
Аналогично для бумеранга.

За время полёта бумеранга средняя скорость его движения и модуль средней скорости равны нулю, так как равно нулю перемещение бумеранга относительно точки А (см. рис.). Но так как путь, который проделал бумеранг, не равен нулю, то и средний модуль скорости движения бумеранга отличен от нуля.

Если посмотреть на правые части формул модуля скорости равномерного движения и среднего модуля скорости переменного движения, то увидим, что правые части равенств одинаковы.

В этом заключается смысл среднего модуля скорости.

Определение 3б. Средний модуль скорости переменного движения равен модулю скорости такого воображаемого равномерного прямолинейного движения, у которого путь и время одинаковы с переменным движением.

Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.

Источник

Неравномерное(переменное) движение. Средняя скорость

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

План-конспект урока по теме « Неравномерное (переменное) движение. Средняя скорость »

Тема: Неравномерное (переменное) движение. Средняя скорость

Образовательная: формирование знаний и представлений о неравномерном (переменном) движении, а также о средней скорости;

Развивающая: развитие и формирование практических умений пользоваться физическими понятиями и величинами для описания равномерного прямолинейного движения; развивать познавательный интерес;

Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.

Тип урока: урок усвоения новых знаний

Оборудование и источники информации:

Исаченкова, Л. А. Физика : учеб. для 7 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2017.

Организационный момент(5 мин)

Актуализация опорных знаний(5мин)

Изучение нового материала (14 мин)

Физкультминутка (1 мин)

Закрепление знаний (15 мин)

Организационный момент (проверка присутствующих в классе, проверка выполнения домашнего задания, озвучивание темы и основных целей урока)

Актуализация опорных знаний

Что выражает график пути?

Для какого движения график пути представляет собой прямую?

Как по графику скорости определить пройденный путь?

Изучение нового материала

Проанализируйте движение автобуса. Он уменьшает скорость перед остановкой. Затем в течение ка кого-то промежутка времени стоит на остановке, т. е. его скорость равна нулю, после чего скорость увеличивается. Значит, скорость автобуса в процессе движения изменяется, т. е. является переменной величиной.

Движение, при котором скорость изменяется, называется неравномерным (переменным).

Практически все движения, наблюдаемые в природе и технике, — неравномерные. С изменяющейся скоростью движутся, например, люди, птицы (рис. 103), дельфины (рис. 104), поезда, падают предметы (рис. 105). Но как же тогда характеризовать это движение?

Неравномерное движение характеризуется средней скоростью. Как определить среднюю скорость? Рассмотрим пример. Вы едете на экскурсию в Брест поездом. Поезд проходит от Минска до Бреста путь s = 330 км. На прохождение этого пути затрачивается время t = 4,5 ч. В течение данного времени поезд стоит на станциях, движется то с увеличивающейся, то с уменьшающейся скоростью.

Среднюю скорость находят путем деления всего пути на весь промежуток времени, за который этот путь пройден. Обозначим среднюю скорость ( v ) и запишем формулу:

Тогда поезд «Минск — Брест» движется со средней скоростью

Вас не удивило, что мы использовали формулу равномерного движения? Да, действительно, формально мы нашли среднюю скорость так, как будто поезд весь путь s = 330 км двигался равномерно с постоянной скоростью v = 73 Это, конечно же, не означает, что он на самом деле двигался равномерно. На отдельных участках пути скорость движения поезда была как значительно

Средняя скорость дает лишь приблизительное представление о быстроте движения тела. Описание переменного движения более сложно по сравнению с описанием равномерного.

Например, если скорость поезда на участке разгона возрастает от 0 до 90 то в различных точках траектории она принимает различные значения из этого промежутка. Таким образом, можно говорить не только о средней скорости на данном участке траектории, но и о скорости в данной точке траектории. Такую скорость называют в физике мгновенной скоростью.

Рассмотрим пример решения задачи со стр. 66

А сейчас поработаем с карточками по теме «Неравномерное (переменное) движение. Средняя скорость» (приложение 1)

Карточка по теме «Неравномерное (переменное) движение. Средняя скорость»

Выполните задания и решите задачи

Заполните таблицу, ответьте устно на контрольные вопросы, решите задачи.

Движение, при кото-ром скорость изменя-ется, называется неравномерным (переменным).

Среднюю скорость находят путем деления всего пути на весь промежуток времени, за который этот путь пройден.

Чем отличается неравномерное движение тела от равномерного?

Ответ: при равномерном движении тело за равное время проходит равное расстояние, а при неравномерном – разное.

Как найти среднюю скорость неравномерного движения?

Какое физическое значение имеют слова «всего» и «весь» в определении средней скорости

Яблоко падало с высоты h = 2,2 м в течение времени t = 0,67 с. Найдите среднее значение скорости падения яблока.

По данным графика (см. рисунок) опишите движение мотоциклиста.

Ответ: сначала мотоциклист за 3 секунды разогнался до скорости 6 м/с, затем 6 секунд ехал с постоянной скоростью равной 6 м/с, а после начал тормозить и через 3,5 секунды остановился.

Итак, подведем итоги:

Характеристикой неравномерного движения является средняя скорость.

Для вычисления средней скорости нужно путь разделить на весь промежуток времени, затраченный на прохождение этого пути.

Организация домашнего задания

§18,ответить на контрольные вопросы.

Определите среднюю скорость своего движения от дома до школы. Оцените полученный результат.

Сегодня на уроке я узнал…

Знания, которые я получил на уроке, пригодятся.

Источник

Неравномерное движение и средняя скорость

теория по физике 🧲 кинематика

Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.

Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.

Средняя векторная скорость

Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.

v _ср — средняя векторная скорость, s — перемещение тела, совершенное за время t

Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.

Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:

Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.

Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:

Средняя скалярная скорость

Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.

v_ср — средняя путевая скорость, s — путь, пройденный телом за время t

Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:

Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.

У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:

Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:

Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.

Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:

Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:

Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:

Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.

Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:

Источник

Кинематика. Скорость.

Скорость характеризует быстроту любых изменений в окружающем мире. Распространение звука или света в воздухе, движение облаков, испарение воды, полет птиц, движение пешеходов по улице – все явления характеризуются определенно скоростью.

Скорость – векторная физическая величина, характеризующая не только быстроту перемещения тела, но и направление его движения.

Скоростью точки называется предел отношения перемещения к промежутку времени Δt, в течение которого это перемещение произошло, при стремлении Δt к нулю:

Такое определение скорости называют также мгновенной скоростью. Оно справедливо и для любых видов движения. Вектор мгновенной скорости всегда направлен по касательной к траектории движения, указывая направление, по которому происходило бы движение тела, если бы с момента времени t на него прекратилось действие других тел.

Понятие средней скорости вводится для характеристики неравномерного движения (движения с переменной скоростью). Определяется она скалярно или векторно.

Когда средняя скорость тела υ_ср равна отношению всего пути Δs ко всему времени движения Δt, то Здесь пройденный путь и время – скалярные величины, следовательно скорость тоже величина скалярная.

Когда средняя скорость тела равна отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло, то Здесь средняя скорость перемещения – векторная величина.

Для неравномерного криволинейного движения векторное определение средней скорости не всегда позволяет определить реальные скорости на пути движения тела. Например, при движении тела по замкнутой траектории в течение некоторого времени его перемещение равно нулю, хотя скорость была отлична от нуля. В таком случае лучше пользоваться скалярным определением скорости.

Источник