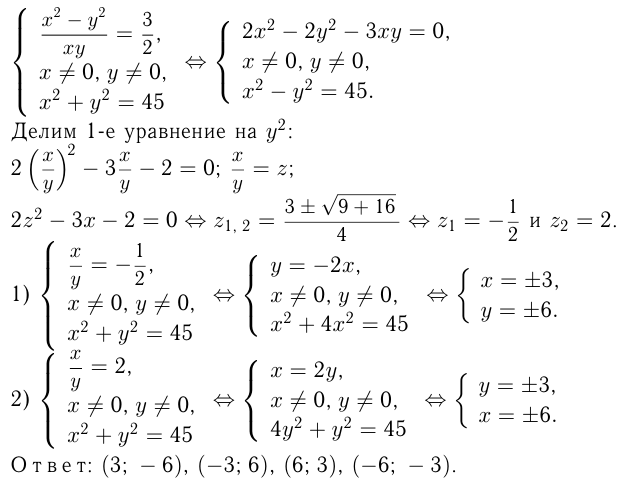Что называют системой уравнений неравенств
Системы неравенств – начальные сведения
В этой статье собрана начальная информация о системах неравенств. Здесь дано определение системы неравенств и определение решения системы неравенств. А также перечислены основные виды систем, с которыми наиболее часто приходится работать на уроках алгебры в школе, и приведены примеры.
Навигация по странице.
Что такое система неравенств?
Системы неравенств удобно определить аналогично тому, как мы вводили определение системы уравнений, то есть, по виду записи и смыслу, вложенному в нее.
Система неравенств – это запись, представляющая собой некоторое число записанных друг под другом неравенств, объединенных слева фигурной скобкой, и обозначающая множество всех решений, являющихся одновременно решениями каждого неравенства системы.
Основные виды систем неравенств
Понятно, что можно составить бесконечно много различных систем неравенств. Чтобы не заблудиться в этом многообразии, их целесообразно рассматривать по группам, имеющим свои отличительные признаки. Все системы неравенств можно разбить на группы по следующим критериям:
По числу неравенств, входящих в запись, различают системы двух, трех, четырех и т.д. неравенств. В предыдущем пункте мы привели пример системы 

Отдельно скажем, что нет смысла говорить о системе одного неравенства, в этом случае по сути речь идет о самом неравенстве, а не о системе.
Что называется решением системы неравенств?
Решением системы неравенств с одной переменной называется такое значение переменной, обращающее каждое из неравенств системы в верное числовое неравенство, другими словами, являющееся решением каждого неравенства системы.
Аналогично можно ввести определение решения системы неравенств с двумя, тремя и большим числом переменных:
Решением системы неравенств с двумя, тремя и т.д. переменными называется пара, тройка и т.д. значений этих переменных, которая одновременно является решением каждого неравенства системы, то есть, обращает каждое неравенство системы в верное числовое неравенство.
Системы неравенств могут не иметь решений, могут иметь конечное число решений, а могут иметь и бесконечно много решений. Часто говорят о множестве решений системы неравенств. Когда система не имеет решений, то имеет место пустое множество ее решений. Когда решений конечное число, то множество решений содержит конечное число элементов, а когда решений бесконечно много, то и множество решений состоит из бесконечного числа элементов.
Из введенных в этой статье определений системы неравенств и ее решений следует, что решение системы неравенств представляет собой пересечение множеств решений всех неравенств этой системы.
Отдельный интерес представляет процесс поиска решений систем неравенств, но прежде чем переходить к нему полезно будет узнать про равносильные системы неравенств.
Системы неравенств: определение, виды, примеры решения
Статья раскрывает тему неравенств, разбираются определения систем и их решения. Будут рассмотрены часто встречающиеся примеры решения систем уравнений в школе на алгебре.
Определение системы неравенств
Системы неравенств определяют по определениям систем уравнений, значит, что особое внимание уделяется записям и смыслу самого уравнения.
Системой неравенств называют запись уравнений, объединенных фигурной скобкой с множеством решений одновременно для всех неравенств, входящих в систему.
Таким же образом определение систем неравенств представлены в школьных учебниках как для использования одной переменной, так и двух.
Основные виды системы неравенств
Имеет место составление бесконечного множества систем неравенств. Их классифицируют по группам, отличающихся по определенным признакам. Неравенства подразделяют по критериям:
Количество входящих неравенств может насчитывать от двух и более. В предыдущем пункте рассматривался пример решения системы с двумя неравенствами.
Рассмотрим решение системы с четырьмя неравенствами.
Решение неравенства отдельно не говорит о решение системы в целом. Для решения системы необходимо задействовать все имеющиеся неравенства.
При записи системы могут быть задействованы уравнения разных видов и с разным количеством переменных. Чаще всего встречаются целые неравенства разных степеней. При подготовке к экзаменам могут встретиться системы с иррациональными, логарифмическими, показательными уравнениями вида:
Такая система включает в себя показательное и логарифмическое уравнение.
Решение системы неравенств
Решение системы неравенств с одной переменной – это значение переменной, которое обращает каждое неравенство заданной системы в верное числовое неравенство, то есть будет являться решением каждого имеющегося неравенства.
Рассмотрим пример решения систем уравнений с одной переменной.
Решение системы неравенств с двумя и более переменными называют значения, которые являются решением всех неравенств при обращении каждого в верное числовое неравенство.
При решении системы неравенств могут давать определенное количество ответов, а могут и бесконечное. Имеется ввиду множество решений такой системы. При отсутствии решений говорят о том, что она имеет пустое множество решений. Если решение имеет определенное число, тогда множества решений имеет конечное число элементов. Если решений много, тогда множество решений содержит бесконечное множество чисел.
Некоторые учебники дают определение частного решения системы неравенств, которое понимается как отдельно взятое решение. А общим решением системы неравенств считают все его частные решения. Такое определение используется редко, поэтому говорят «решение системы неравенств».
Данные определения систем неравенств и решения рассматриваются как пересечения множеств решений всех неравенств системы. Особое внимание стоит уделить разделу, посвященному равносильным неравенствам.
Совокупности уравнений, неравенств, систем: определение, как решить
В данной статье мы сформулируем общее понятие совокупностей неравенств, уравнений и их систем, а также их комбинации. Кроме определений здесь, как обычно, есть решения задач, наглядно поясняющие тот или иной фрагмент текста.
Понятие совокупности
Проанализировав несколько учебников, выберем наиболее удачное определение:
Совокупность уравнений представляет собой несколько уравнений, записанных друг под другом и объединенных квадратной скобкой. Значение этой записи таково: совокупность объединяет такие значения переменных, при которых хотя бы одно из входящих в нее уравнений превращается в верное равенство.
Сравним между собой понятие совокупности и понятие системы:
Вот примеры совокупности уравнений:
Понятие совокупности неравенств формулируется схожим образом.
Совокупность неравенств представляет собой несколько неравенств, записанных друг под другом и объединенных квадратной скобкой. Она включает в себя решения, которые подходят хотя бы для одного из неравенств, входящих в состав совокупности.
Приведем пример такой записи:
Схожее определение для этого понятия упоминается в учебнике Мордковича.
В качестве примера смешанных совокупностей приведем две:
Что такое решение совокупности
Решение совокупности с одной переменной представляет собой значение этой переменной, которое является решением хотя бы одной составляющей совокупности (уравнения, неравенства).
Возьмем еще один пример, посложнее. У нас есть совокупность:
Также нужно отметить следующее: объединение решений всех компонентов совокупности также есть решение совокупности. Напомним, что решение системы представляет собой пересечение решений ее компонентов.
В продолжение темы мы советуем вам материал «Равносильные совокупности».
Неравенство. Система линейных неравенств.
Системой линейных неравенств называется любая совокупность двух или более линейных неравенств, содержащих одну и туже неизвестную величину
Вот образцы подобных систем:
Решить систему неравенств означает установить все значения неизвестной величины, при которых реализуются все неравенство системы, либо доказать, что таких не существует.
Все решения системы неравенств формируют множество решений. Если система неравенств не реализуется ни при каких значениях х, то обозначают, что такие системы неравенств несовместимы.
Установим область определения функции .
Область определения или область допустимых значений –это множество всех х при которых функция существует.
Функция существует, когда существуют оба квадратных корня, т.е. под корнем стоит не отрицательное число.
Как рассчитать такую систему? Следует установить все x, одновременно выполняющие условия и первого и второго неравенства.
Воспроизведем на оси x множество решений первого и второго неравенства.
Промежуток пересечения двух лучей и есть наше решение. Следовательно решением данного неравенства выступают все х расположенные между двойкой и восьмеркой.
Ответ: х[2;8]
Применение такого типа отображения решения системы неравенств иногда именуют методом крыш.
Определение: Пересечением двух множеств А и В называется такое третье множество, которое включает все элементы, входящих и в А и в В. Это смысл пересечения множеств произвольной природы. Нами сейчас детально рассматриваются числовые множества, поэтому при нахождении линейных неравенств такими множествами являются лучи – сонаправленные, противонаправленные и так далее.
Выясним на реальных примерах нахождение линейных систем неравенств, как определить пересечения множеств решений отдельных неравенств, входящих в систему.
Вычислим систему неравенств:
1.
Поместим одну под другой две силовые прямые. На верхней нанесем те значения х, которые выполняют первое неравенство x>7, а на нижней – которые выступают решением второго неравенства x>10 Соотнесем результаты числовых прямых, выясним, что оба неравенства будут удовлетворятся при x>10.
2.
4.Решить систему
Откуда может взяться второе неравенство системы? Например, из неравенства x 2 + 1 ≥ 0,
Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.
Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно отбросить.
5.
Ответ:x система противоречива.
Системы уравнений и неравенств
Если какие-либо уравнения или неравенства объединены фигурной скобкой в систему, то предполагается, что они должны быть выполнены одновременно, т.е. решениями системы могут быть только такие значения неизвестных, которые удовлетворяют всем уравнениям и неравенствам, входящим в систему.
Если система уравнений или неравенств имеет решения, то говорят, что она совместна, если она решений не имеет, то — несовместна.
Системы называются равносильными, если множества их решений совпадают. Основу решения системы составляют равносильные преобразования входящих в нее уравнений и неравенств. Поскольку система включает, как правило, не одну неизвестную величину, а две, три и, возможно, больше, то для исключения неизвестных и приведения системы к уравнениям и неравенствам с одной неизвестной используют такой прием как подстановка. Если из одного уравнения можно выразить одну неизвестную через другую, а затем подставить ее в другое уравнение, то это хороший способ решения, нужно только помнить об ограничениях. Однако это нелегко сделать сразу, требуются дополнительные преобразования.
Можно складывать и вычитать уравнения системы с целью исключения одной из неизвестных. Решение системы записывается следующим образом: если в системе две неизвестных х и у, то (х; у), если три неизвестных х, у, z, то (х; у; z) и т. п. В системах, так же как и в уравнениях, используются разложение на множители, замена переменных.
Умение решать системы важно при решении текстовых задач и часто является наиболее трудоемкой частью решения.
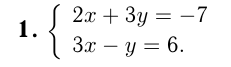
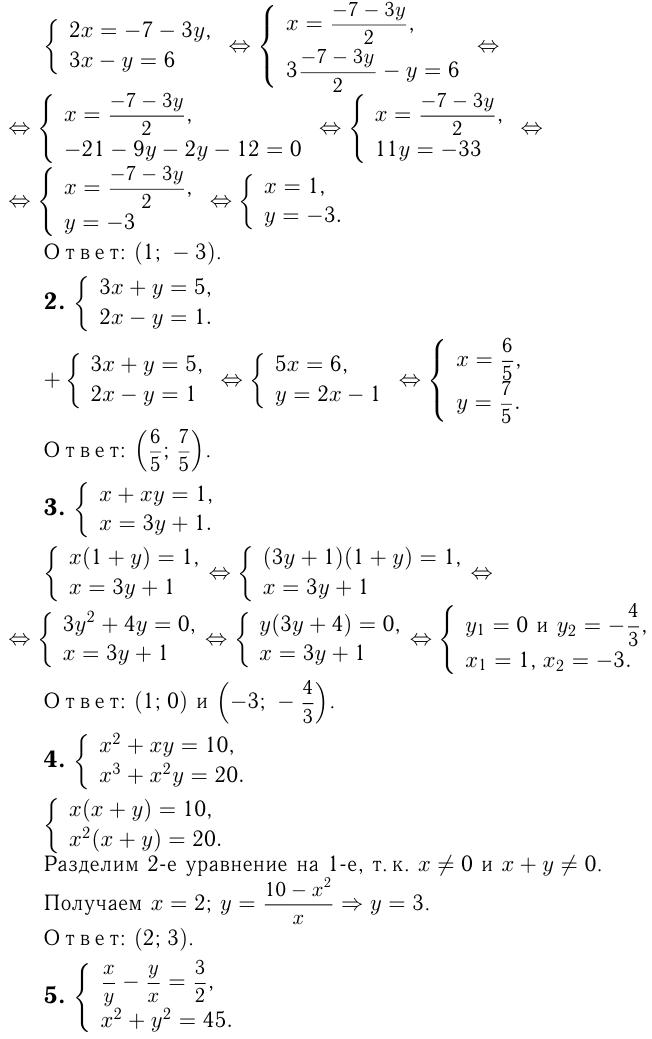
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института