Что называют произведением числа а на натуральное число b не равно 1
ВОПРОСЫ
1. Что называют произведением числа a на натуральное число b, не равное 1?
Произведением числа а на натуральное число b, не равное 1, называют сумму, состоящую из b слагаемых, каждое из которых равно а.
2. Как в равенстве а•b =с называют число а? Число b? Число с? Выражение а•b?
3. Чему равно произведение двух множителей, один из которых равен 1?
4. Чему равно произведение двух множителей, один из которых равен 0?
5. Каким свойством обладают множители, произведение которых равно нулю?
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
6. Сформулируйте переместительное свойство умножения.
От перестановки мест множителей произведение не меняется.
7. Как записывают в буквенном виде переместительное свойство умножения?
РЕШАЕМ УСТНО
1. Чему равна сумма:
2. Вычислите:
3. Найдите произведение чисел 14 и 6.
4. Увеличьте число 18 в 3 раза.
5. Найдите длину боковой стороны равнобедренного треугольника, если его периметр на 12 см больше основания.
7. Найдите периметр квадрата, если он больше его стороны на 18 см.
УПРАЖНЕНИЯ
384. Запишите сумму в виде произведения:
385. Выполните умножение:
386. Выполните умножение:
387. Вычислите:
388. Вычислите:
389. Вычислите значение выражения:
390. Вычислите значение выражения:
391. Выполните умножение:
392. Выполните умножение:
393. Готовясь к школе, Буратино купил 34 тетради по 12 сольдо и 18 тетрадей по 16 сольдо. Сколько сольдо заплатил Буратино за все тетради?
394. Кот Матроскин продал 42 л молока по 64 р. за 1 литр и 16 кг творога по 320 р. за 1 килограмм. Сколько денег выручил Матроскин за свой товар?
395. В походе, длившемся несколько дней, турист 14 ч плыл по реке на лодке со скоростью 8 км/ч и шёл пешком 23 ч со скоростью 4 км/ч. Какой путь, по реке или суше, был длиннее и на сколько километров?
396. Путешественник плыл на моторной лодке 5 ч по реке со скоростью 27 км/ч и 7 ч по озеру со скоростью 21 км/ч. Какой путь, по реке или по озеру, был длиннее и на сколько километров?
397. В школу завезли апельсины, мандарины и лимоны. Апельсинов было 94 кг, что в 7 раз меньше, чем мандаринов, и на 16 кг больше, чем лимонов. Сколько всего килограммов фруктов завезли в школу?
398. Школе для кабинета музыки выделили 50 000 р. на покупку компьютера, музыкального центра и мультимедиапроектора. Музыкальный центр стоит 3 600 р., что в 4 раза меньше стоимости компьютера и на 2 800 р. меньше стоимости мультимедиапроектора. Хватит ли выделенных денег на покупку?
399. Найдите значение выражения:
400. Найдите значение выражения:
404. Из одного города в противоположных направлениях одновременно выехали два автомобиля. Скорость одного из них была 74 км/ч, что на 8 км/ч больше, чем скорость другого. Какое расстояние будет между ними через 7 ч после начала движения?
406. Из двух сёл одновременно навстречу друг другу отправились велосипедист и пешеход. Пешеход шёл со скоростью 3 км/ч, что в 4 раза меньше скорости велосипедиста. Найдите расстояние между сёлами, если велосипедист и пешеход встретились через 3 ч после начала движения.
407. Всегда ли произведение двух натуральных чисел больше, чем их сумма?
Не всегда произведение двух натуральных чисел больше, чем их сумма.
410. Вместо звёздочек поставьте цифры так, чтобы умножение было выполнено верно:
411. Вместо звёздочек поставьте цифры так, чтобы умножение было выполнено верно:
412. При каких значениях а верно равенство:
413. Сумма и произведение четырёх натуральных чисел равны 8. Найдите эти числа.
414. В записи 1* 2* 3* 4* 5 замените звёздочки знаками «+» или «•» и расставьте скобки так, чтобы значение полученного выражения равнялось 100.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
ЗАДАЧА ОТ МУДРОЙ СОВЫ
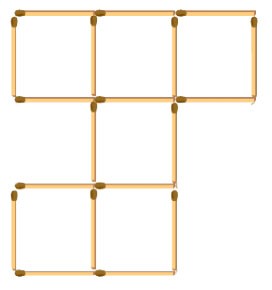
419. 1) Сложите из десяти спичек три квадрата. 2) Сложите из 19 спичек шесть квадратов. 3) Какие четыре спички надо убрать (рис. 142), чтобы остались пять квадратов?
Мерзляк 5 класс — § 16. Умножение. Переместительное свойство умножения
Вопросы к параграфу
1. Что называют произведением числа а на натуральное число b, не равное 1?
Произведением числа а на натуральное число b, не равное 1, называют сумму, состоящую из b слагаемых, каждое из которых равно а.
2. Как в равенстве а • b = с называют число а? Число b? Число с? Выражение а • b?
3. Чему равно произведение двух множителей, один из которых равен 1?
Произведение равно другому множителю: а • 1 = 1 • а = а.
4. Чему равно произведение двух множителей, один из которых равен 0?
Произведение равно нулю: а • 0 = 0 • а = 0.
5. Каким свойством обладают множители, произведение которых равно нулю?
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
6. Сформулируйте переместительное свойство умножения.
От перестановки множителей произведение не меняется.
7. Как записывают в буквенном виде переместительное свойство умножения?
Решаем устно
1. Чему равна сумма:
2. Вычислите:
3. Найдите произведение чисел 14 и 6.
4. Увеличьте число 18 в 3 раза.
5. Найдите длину боковой стороны равнобедренного треугольника, если его периметр на 12 см больше основания.
Если периметр равнобедренного треугольника на 12 см больше основания, то длина обеих боковых сторон этого треугольника равна 12 см. В равнобедренном треугольнике боковые стороны равны. Значит:
12 : 2 = 6 (см) — длина боковой стороны равнобедренного треугольника.
6. Определите вид треугольника, две стороны которого равны 8 см и 12 см, а периметр — 28 см.
28 — 8 — 12 = 20 — 12 = 8 (см) — длина третьей стороны треугольника.
Мы видим, что длина третьей стороны совпадает с длиной ещё одной стороны треугольника. Треугольник, у которого две стороны равны, называется равнобедренным.
Ответ: Это равнобедренный треугольник.
7. Найдите периметр квадрата, если он больше его стороны на 18 см.
Периметр квадрата равен сумме длин всех его сторон. Если периметр на 18 см больше длины одной из сторон, значит сумма длин всех оставшихся сторон равна 18 см. У квадрата все стороны равны. Значит:
18 : 3 = 6 (см) — длина стороны квадрата
6 • 4 = 24 (см) — периметр этого квадрата.
Упражнения
384. Запишите сумму в виде произведения:
385. Выполните умножение:
386. Выполните умножение:
387. Вычислите:
388. Вычислите:
389. Вычислите значение выражения:
1) 17x + 432, если х= 58

2) (739 — х) • у, если х = 554, у = 4 900
390. Вычислите значение выражения:
1) 976 — 24x, если х = 36
2) х • 63 — у, если х = 367, у = 19 742
391. Выполните умножение:
392. Выполните умножение:
393. Готовясь к школе, Буратино купил 34 тетради по 12 сольдо и 18 тетрадей по 16 сольдо. Сколько сольдо заплатил Буратино за все тетради?
394. Кот Матроскин продал 42 л молока по 64 р. за 1 литр и 16 кг творога по 320 р. за 1 килограмм. Сколько денег выручил Матроскин за свой товар?
Ответ: 7 808 рублей.
395. В походе, длившемся несколько дней, турист 14 ч плыл по реке на лодке со скоростью 8 км/ч и шёл пешком 23 ч со скоростью 4 км/ч. Какой путь, по реке или по суше, был длиннее и на сколько километров?
1) 8 • 14 = 112 (км) — турист проплыл на лодке.
2) 4 • 23 = 92 (км) — турист прошёл пешком.
3) 112 км > 92 км — путь по реке бы длиннее, чем по суше.
4) 112 — 92 = 20 (км) — на столько километров путь по реке был длиннее, чем по суше.
Ответ: На 20 километров путь по реке был длиннее, чем по суше.
396. Путешественник плыл на моторной лодке 5 ч по реке со скоростью 27 км/ч и 7 ч по озеру со скоростью 21 км/ч. Какой путь, по реке или по озеру, был длиннее и на сколько километров?
1) 27 • 5 = 135 (км) — путешественник проплыл по реке.
2) 21 • 7 = 147 (км) — путешественник проплыл по озеру.
3) 147 км > 135 км — путь по озеру бы длиннее, чем по реке.
4) 147 — 135 = 12 (км) — на столько километров путь по озеру был длиннее, чем по реке.
Ответ: На 12 километров путь по озеру был длиннее, чем по реке.
397. В школу завезли апельсины, мандарины и лимоны. Апельсинов было 94 кг, что в 7 раз меньше, чем мандаринов, и на 16 кг больше, чем лимонов. Сколько всего килограммов фруктов завезли в школу?
1) 94 • 7 = 658 (кг) — мандаринов завезли в магазин.
2) 94 — 16 = 78 (кг) — лимонов завезли в магазин.
3) 94 + 658 + 78 = 830 (кг) — фруктов завезли в магазин всего.
398. Школе для кабинета музыки выделили 50 000 р. на покупку компьютера, музыкального центра и мультимедиапроектора. Музыкальный центр стоит 3 600 р., что в 4 раза меньше стоимости компьютера и на 28 200 р. меньше стоимости мультимедиапроектора. Хватит ли выделенных денег на покупку?
1) 3 600 • 4 = 14 400 (рублей) — стоимость компьютера.
2) 3 600 + 28 200 = 31 800 (рублей) — стоит мультимедиапроектор.
3) 3 600 + 14 400 + 31 800 = 49 800 (рублей) — потребуется на все покупки.
Ответ: Да, выделенный денег на покупку хватит.
399. Найдите значение выражения:
400. Найдите значение выражения:
401. Из одного порта в другой одновременно отправились теплоход и катер. Скорость теплохода составляет 28 км/ч, а скорость катера — 36 км/ч. Какое расстояние будет между ними через 5 ч после начала движения?
1) 28 • 5 = 140 (км) — пройдёт за 5 часов теплоход.
2) 36 • 5 = 180 (км) — пройдёт за 5 часов катер.
3) 180 — 140 = 40 (км) — будет расстояние между теплоходом и катером через 5 часов.
402. Из одного села в одном направлении одновременно выехали два велосипедиста. Один из них ехал со скоростью 12 км/ч, а второй — 9 км/ч. Какое расстояние будет между ними через 6 ч после начала движения?
1) 12 • 6 = 72 (км) — проедет за 6 часов первый велосипедист.
2) 9 • 6 = 54 (км) — проедет за 6 часов второй велосипедист.
3) 72 — 54 = 18 (км) — будет расстояние между первым и вторым велосипедистом через 6 часов.
403. С одной станции в противоположных направлениях одновременно отправились два поезда. Один из них двигался со скоростью 64 км/ч, а второй — 57 км/ч. Какое расстояние будет между ними через 9 ч после начала движения?
1) 64 • 9 = 576 (км) — проедет за 9 часов первый поезд.
2) 57 • 9 = 513 (км) — проедет за 9 часов второй поезд.
3) 576 + 513 = 1089 (км) — будет расстояние между первым и вторым поездом через 9 часов.
404. Из одного города в противоположных направлениях одновременно выехали два автомобиля. Скорость одного из них была 74 км/ч, что на 8 км/ч больше, чем скорость другого. Какое расстояние будет между ними через 7 ч после начала движения?
1) 74 • 7 = 518 (км) — проедет за 7 часов первый автомобиль.
2) 74 — 8 = 66 (км) — скорость второго автомобиля.
3) 66 • 7 = 462 (км) — проедет за 7 часов второй автомобиль.
3) 518 + 462 = 980 (км) — будет расстояние между первым и вторым автомобилем через 7 часов.
405. Из двух городов одновременно навстречу друг другу выехали велосипедист и легковой автомобиль. Велосипедист ехал со скоростью 11 км/ч, а автомобиль — в 7 раз быстрее. Найдите расстояние между городами, если велосипедист и автомобиль встретились через 4 ч после начала движения.
1) 11 • 7 = 77 (км/ч) — скорость движения автомобиля.
2) 11 • 4 = 44 (км) — проехал велосипедист за 4 часа.
3) 77 • 4 = 308 (км) — проехал автомобиль за 4 часа.
4) 44 + 308 = 352 (км) — расстояние между городами.
406. Из двух сёл одновременно навстречу друг другу отправились велосипедист и пешеход. Пешеход шёл со скоростью 3 км/ч, что в 4 раза меньше скорости велосипедиста. Найдите расстояние между сёлами, если велосипедист и пешеход встретились через 3 ч после начала движения.
1) 3 • 4 = 12 (км/ч) — скорость движения велосипедиста.
2) 3 • 3 = 9 (км) — прошёл пешеход за 3 часа.
3) 12 • 3 = 36 (км) — проехал велосипедист за 3 часа.
4) 9 + 36 = 45 (км) — расстояние между сёлами.
407. Всегда ли произведение двух натуральных чисел больше, чем их сумма?
408. Как изменится произведение двух натуральных чисел, если:
409. Из двух посёлков, расстояние между которыми равно 3 км, одновременно навстречу друг другу вышли два пешехода. Один из них двигался со скоростью 5 км/ч, а второй — 4 км/ч. Какое расстояние будет между пешеходами через 2 ч после начала движения?
1) 5 • 2 = 10 (км) — пройдет за 2 часа первый пешеход.
2) 4 • 2 = 8 (км) — пройдет за 2 часа второй пешеход.
3) 10 + 8 — 3 = 15 (км) — будет расстояние между пешеходами через 2 часа.
Комментарий: В последнем действии необходимо отнять 3 км, так как это расстояние пройдёт и первый, и второй пешеход. То есть, если просто сложить километры, пройденные пешеходами, то расстояние между посёлками будет посчитано дважды.
410. Вместо звёздочек поставьте цифры так, чтобы умножение было выполнено верно:
411. Вместо звёздочек поставьте цифры так, чтобы умножение было вы полнено верно:
Комментарий: в учебнике допущена опечатка — в примере № 2 на месте числа 74 звёздочки сдвинуты на одну клетку левее, чем нужно.
412. При каких значениях а верно равенство:
413. Сумма и произведение четырёх натуральных чисел равны 8. Найдите эти числа.
414. В записи 1 * 2 * 3 * 4 * 5 замените звёздочки знаками «+» или «-» и расставьте скобки так, чтобы значение полученного выражения равнялось 100.
Упражнения для повторения
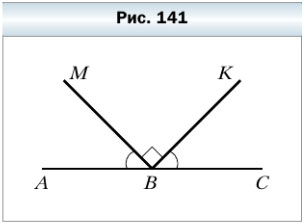
415. Найдите величину угла АВМ (рис. 141), если ∠MBK — прямой и ∠ABM = ∠CBK.
∠АBС = 180º — развёрнутый
∠ABM = ∠CBK = (∠АBС — ∠MBK) : 2 = (180º — 90º) : 2 = 90º : 2 = 45º.
Ответ: ∠ABM = ∠CBK = 45º.
416. Угол ABC равен 72º, луч BD — биссектриса угла ABC, луч BE — биссектриса угла ABD. Вычислите величину угла СВЕ.
1) Так как луч BD — биссектриса ∠ABC, то
∠ABD = ∠BDC = 72º : 2 = 36º
2) Так как луч BE — биссектриса угла ∠ABD, то
∠ABE = ∠EBD = 36º : 2 = 18º
3) ∠СВЕ = ∠BDC + ∠EBD = 36º + 18º = 54º
417. По формуле а = b : 4 — 6 найдите значение а, если:
418. Сумма длин первой и второй сторон треугольника равна 33 см, первой и третьей — 39 см, второй и третьей — 42 см. Найдите периметр треугольника.
Пусть длина первой стороны треугольника равна а см, длина второй стороны треугольника равна b см, а длина третьей стороны треугольника равна с см. Тогда мы можем записать:
(а + b) + (а + с) + (b + с) = 33 + 39 + 42 = 114 (см)
Применим переместительное свойство сложения:
(а + b) + (а + с) + (b + с) = а + b + а + с + b + с = (а + b + с) + (а + b + с) = 114 (см).
Мы знаем, что периметр P = а + b + с. Значит можно записать:
P + P = 144 (см), то есть
Задача от мудрой совы
419. 1) Сложите из десяти спичек три квадрата.
2) Сложите из 19 спичек шесть квадратов.
3) Какие четыре спички надо убрать (рис. 142), чтобы остались пять квадратов?