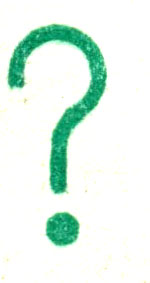Что называют проекцией связи
Что называют проекцией связи
§ 18. Комплектный чертеж
Изучив, как в прямоугольных проекциях изображают точки, отрезки прямых и плоские фигуры, т. е. элементы, которые образуют различные предметы, рассмотрим способы получения прямоугольных проекций самих предметов.
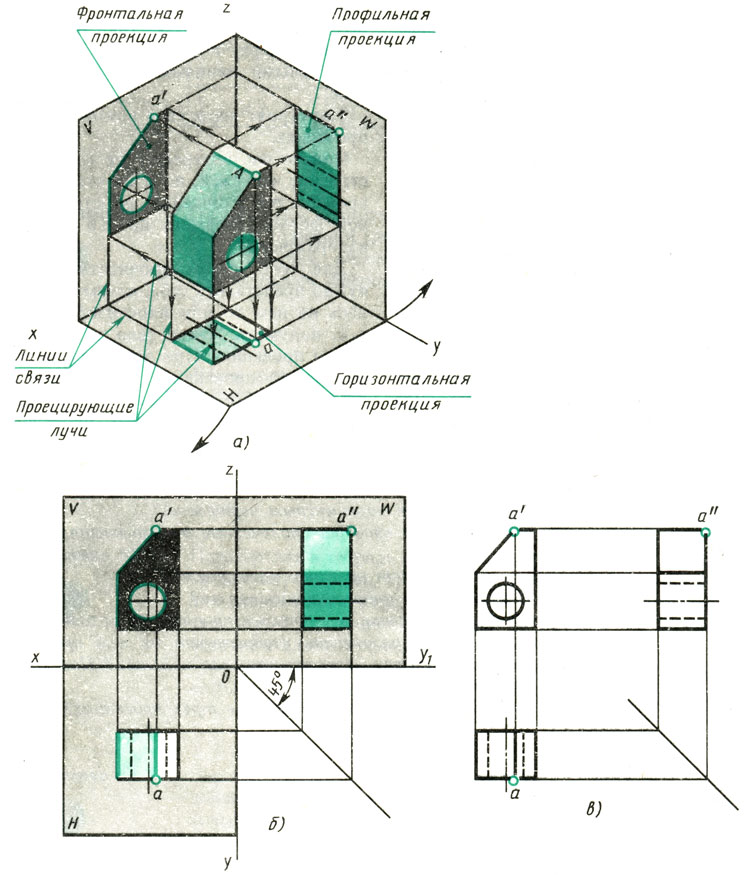
Изображаемый предмет располагают перед плоскостями трехгранного угла так, чтобы возможно большее число граней предмета было параллельно плоскостям (рис. 112, а). Предмет проецируют на фронтальную плоскость V. Грани, параллельные плоскости V, изобразятся в натуральную величину, а грани, перпендикулярные к плоскости V,- отрезками прямых линий. Ребра, параллельные плоскости V, изобразятся в виде линии в натуральную длину, а ребра, перпендикулярные плоскости F,- точками. Так получают фронтальную проекцию предмета или вид спереди (см. рис. 112, а). Тем же способом на плоскости Н получают горизонтальную проекцию (вид сверху). Профильная проекция предмета (вид слева) расположится на плоскости W. Развернув плоскости проекции, получают комплексный чертеж (рис. 112, в).
Рис. 112. Получение комплексного чертежа
Фронтальную проекцию называют видом спереди, или главным видом. Главный вид, получаемый на фронтальной плоскости проекций, является исходным, он должен давать наиболее полное представление о форме и размерах предмета. Остальные проекции располагаются в зависимости от главного вида. Такое расположение проекций называют проекционной связью.
Проекционная связь показана на рис. 112, б и в тонкими сплошными линиями, которые называются линиями связи.
При проведении линий связи между горизонтальной и профильной проекциями удобно пользоваться вспомогательной прямой, которую проводят под углом 45° примерно на уровне вида сверху, правее его (рис. 112, б и в). Линии связи, идущие от вида сверху, доводят до вспомогательной прямой. Из точек пересечения с нею восставляют перпендикуляры для построения вида слева.
Чтобы сократить число изображений, допускается на видах показывать невидимые части поверхности предмета штриховыми линиями. Так, например, на виде сверху и слева (рис. 112, б и в) штриховыми линиями показано отверстие.
Так строят чертежи в прямоугольных проекциях.
Однако нас интересует не только построение чертежей, но и их чтение, т. е. процесс представления пространственной формы предмета по его плоским изображениям.
Для того чтобы прочитать чертеж, нужно представить себе, почему получилось на нем то или иное изображение, т. е. подумать, какое тело могло дать такую проекцию. При этом нельзя рассматривать проекции отдельно одну от другой. Необходимо мысленно объединить представления о всех проекциях, данных на чертеже.
Ответьте на вопросы
1. Что называют комплексным чертежом?
2. Как называют проекции, полученные на плоскостях V, Н, W?
3. Как располагают проекции на чертеже?
4. Что означает «проекционная связь»?
5. Какое изображение на чертеже принято за исходное (основное)? В каком положении изображают на нем предмет?
6. Для чего служит «вспомогательная прямая»? Под каким углом ее проводят?
7. Как строят чертеж: предмета в трех проекциях?
Задания к § 17 и 18
Упражнение 50
Рассмотрите рис. 113, а и б. Выпишите в рабочую тетрадь названия плоскостей проекций, изображений и других элементов прямоугольного проецирования, помеченных на рис. 113 цифрами или буквами.
Форма записи:
Рис. 113. Задание для упражнений
Упражнение 51
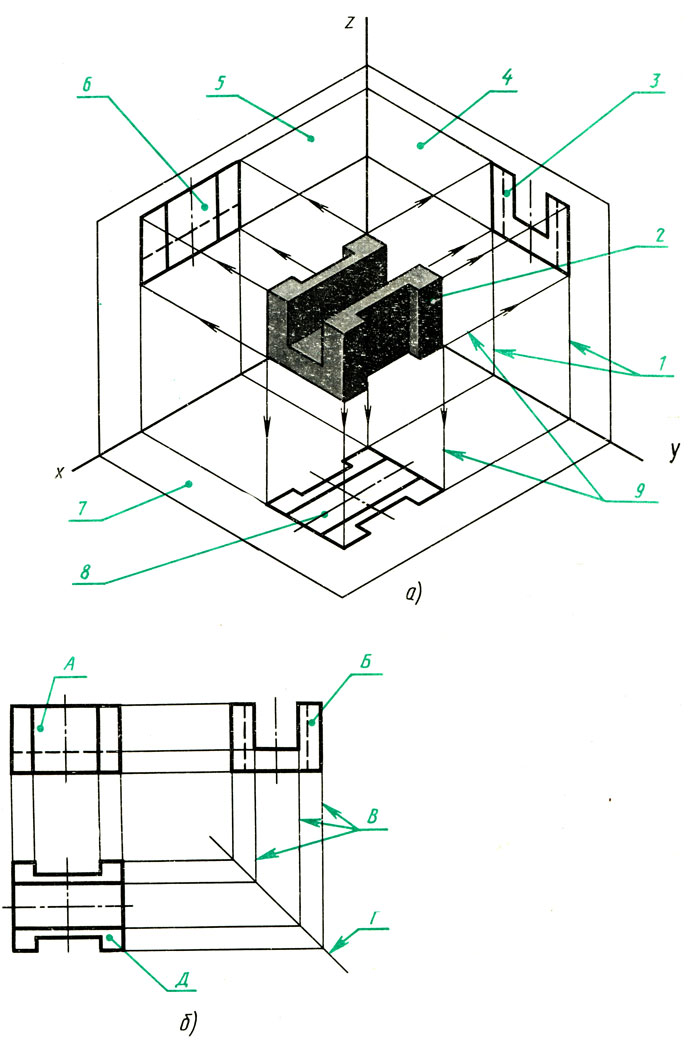
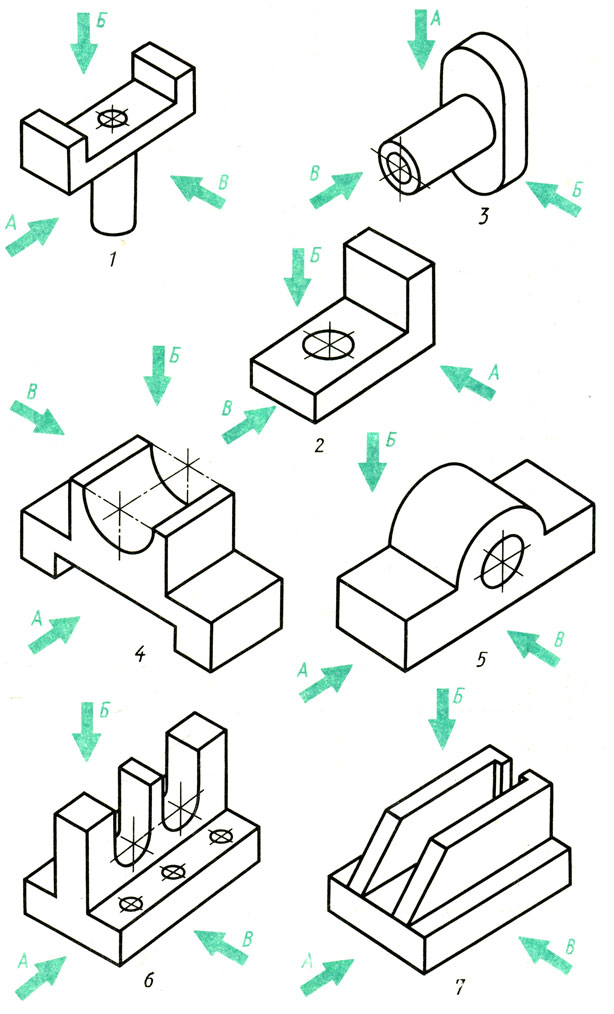
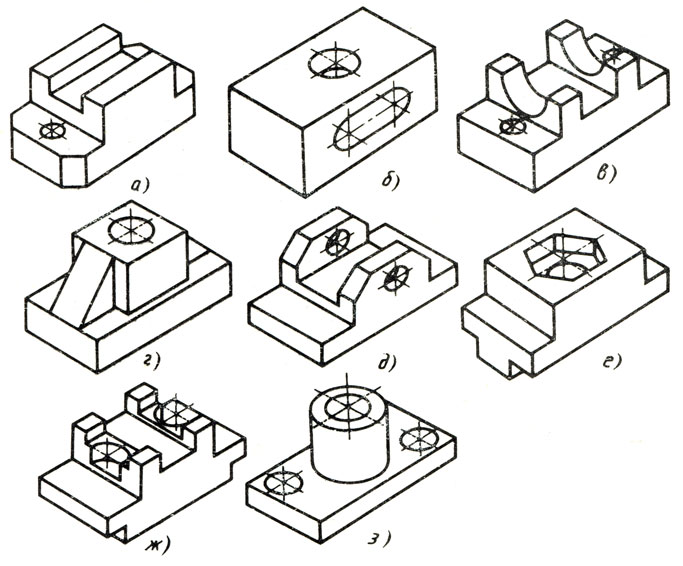
По рисункам предметов найдите их чертежи в системе прямоугольных проекций (рис. 114). Запишите в рабочей тетради, какому рисунку, обозначенному буквой, соответствует чертеж, обозначенный цифрой. Как называют виды, данные на чертеже?
Форма записи:
Рис. 114. Задание для упражнений
Упражнение 52
Перечертите в тетрадь рис. 112, в в масштабе 2 : 1. Дайте к этому рисунку подпись, кратко изложите в ней основные положения данного параграфа (что называют комплексным чертежом, что значит проекционная связь, под каким углом проводят вспомогательную прямую и каково ее назначение, как обозначают проекции точек, как строят комплексный чертеж). В начале работы напишите заголовок «Комплексный чертеж».
Упражнение 53
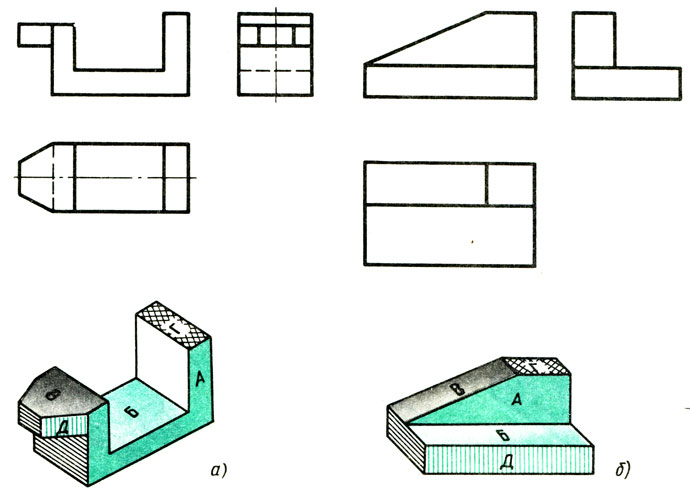
Перечертите рис. 115, я и б в масштабе 2 : 1. Раскрасьте на каждой из прямоугольных проекций одну и ту же поверхность одинаковым цветом. (Поверхность надо раскрасить цветным карандашом или краской на всех проекциях независимо от того, изображается она фигурой или линией.)
Рис. 115. Задание для раскрашивание проекций
Упражнение 54
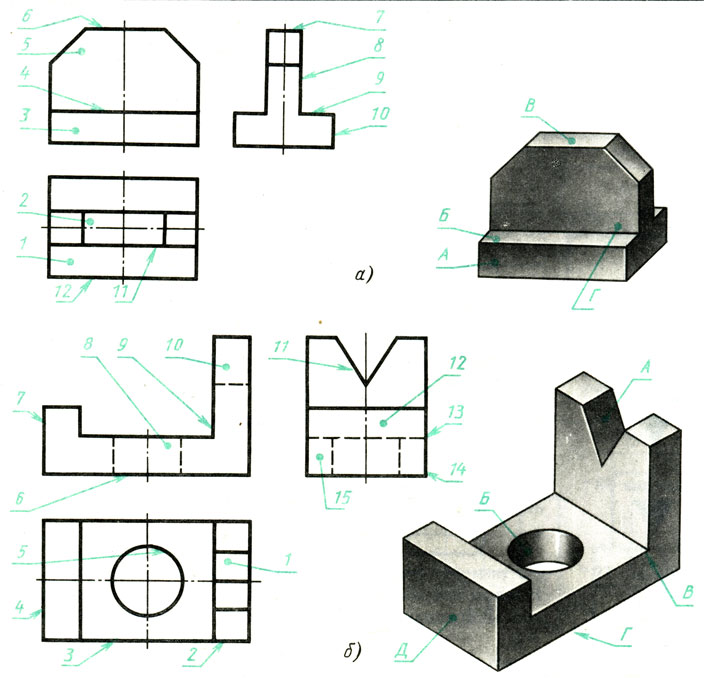
Определите и запишите в рабочей тетради, какой поверхности детали, обозначенной буквой на наглядном изображении, соответствуют линии и фигуры, обозначенные цифрами на чертеже (рис. 116, а и б).
Форма записи
Рис. 116. Задание на нахождение проекций поверхностей предметов
Упражнение 55
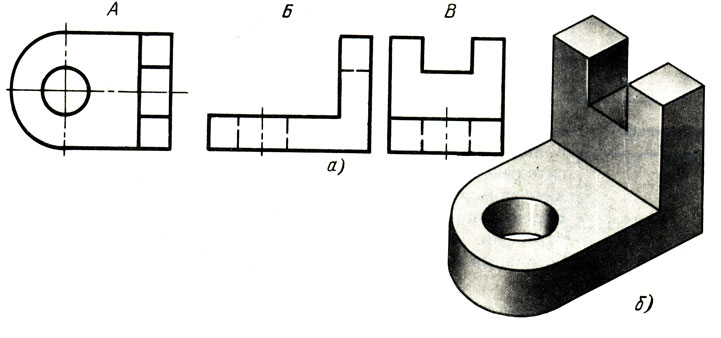
На рис. 117, а виды расположены без системы. Определите, какой буквой помечен главный вид. Как относительно главного вида должны быть расположены остальные виды? Решить задачу вам поможет наглядное изображение, приведенное на рис. 117, б.
Рис. 117. Задание на расположение видов чертежа в проекцтонной связи
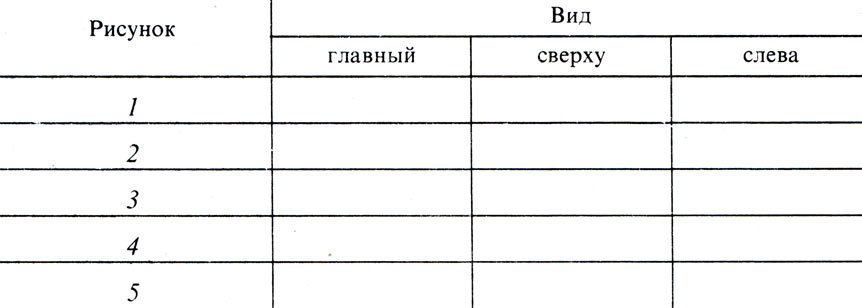
Упражнение 56
Форма записи:
Рис. 118. Задания на определение видов и правильное их расположение не чертеже
Упражнение 57
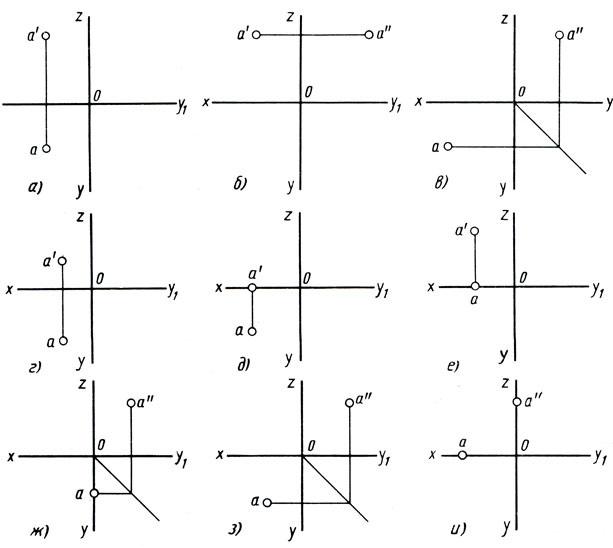
По заданным двум проекциям точек (рис. 119, а-и) найдите ушш третьи проекции. Обозначьте их буквами.
Рис. 119. Задание на построение третьих проекций точек
Упражнение 58
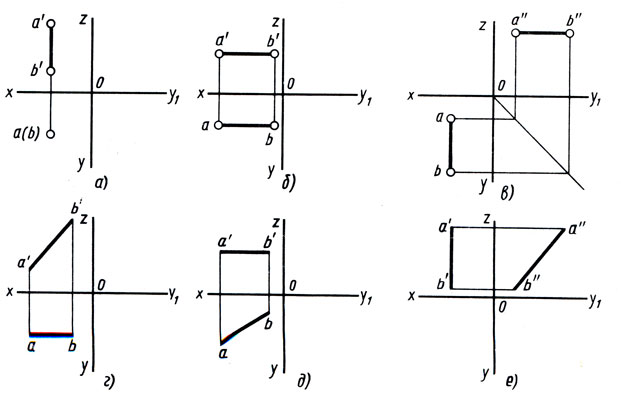
По заданным двум проекциям отрезков прямых (рис. 120, а-е) найдите третьи проекции. Обозначьте их буквами.
Рис. 120. Задания на построение третьих проекций линий
Упражнение 59
Форма записи:
Рис. 121. Задания на выбор положения детали для главного вида
Упражнение 60
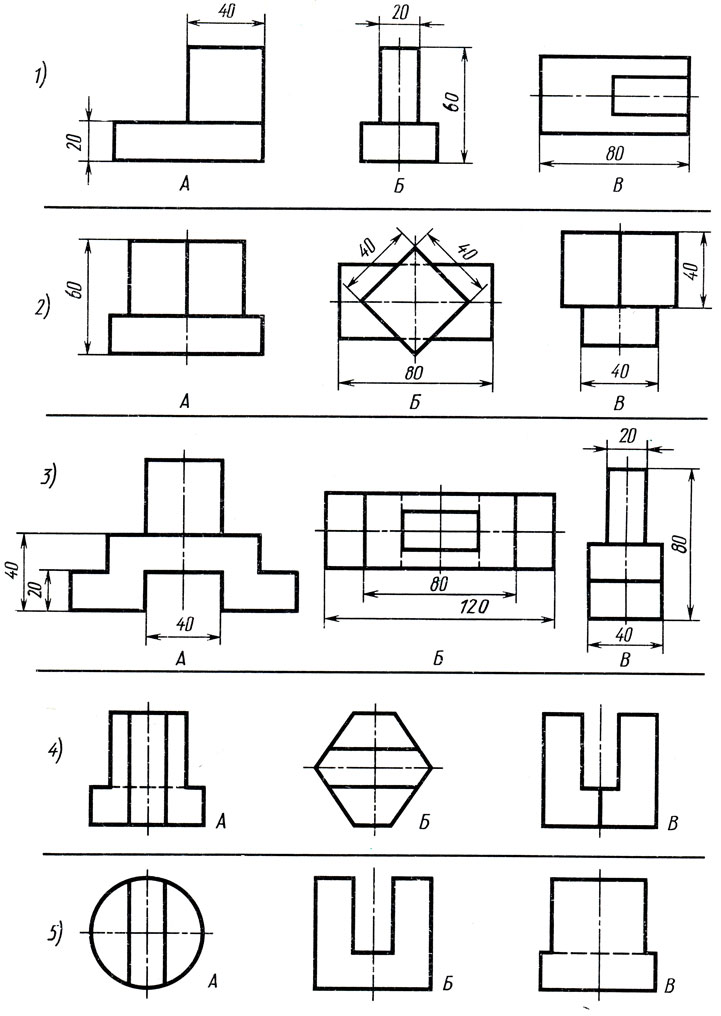
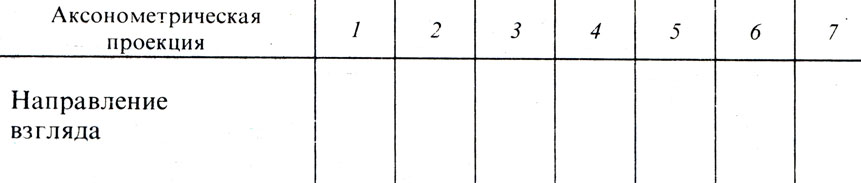
Рис. 122. Задания на построение комплексных чертежей по аксонометрическим проекциям
Упражнение 61
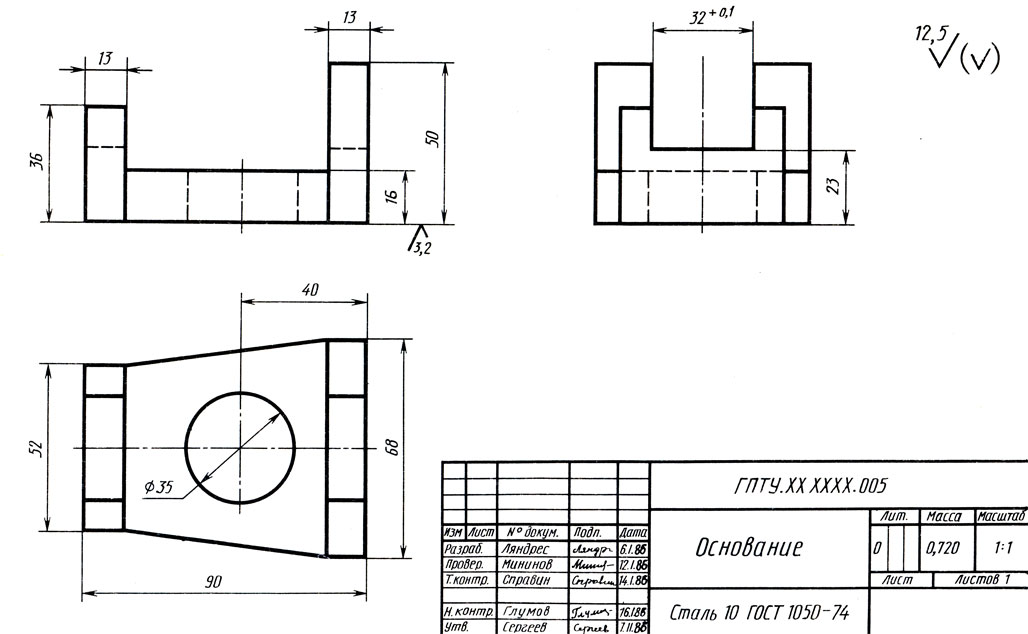
Письменно ответьте на вопросы к рис. 123 (вопросы не переписывайте):
Рис. 123. Задания для упражнений
1. Как называется деталь?
2. Из какого материала ее надо изготовить?
3. В каком масштабе выполнен чертеж?
4. Какие виды даны на чертеже?
6. Каковы габаритные размеры детали?
7. Какова шероховатость поверхности отверстия? Какими размерами определяется положение отверстия?
8. Какова шероховатость основания детали?
9. Что изображено горизонтальной штриховой линией на виде слева? На каком расстоянии от основания детали проходит эта линия? Почему края этой линии заканчиваются отрезками сплошной основной линии, а не штриховой?
Что такое проекционная связь?
На чертеже объект отображается различными проекциями. Одна и та же точка на разных проекциях строится с помощью линий, которые называются линии связи. Эти вспомогательные линии нужны только для проведения построений, после которых их стирают. При большом опыте чертежи выполняются без построения вспомогательных линий.
В базисном учебном плане предмета черчение вообще нет. Этот предмет вводят либо как элективный курс, либо в профильных классах. К сожалению, Минобрнауки считает этот предмет ненужным, хотя опыт показывает, что в ВУЗах преподаватели бьют тревогу, т.к. вчерашние школьники совершенно не изучали черчения и не могут сделать элементарные чертежи. Однако, ситуация не меняется. Черчения как обязательного предмета в школах РФ нет.
Проектируя модель детали в Компас 3Д мы стремимся к тому, чтобы из неё создать точный чертеж, при помощи операции «создать чертеж из модели».
Когда мы выбираем эту функцию, то на новом листе получаем один из главных видов нашей детали. Дальше, пользуясь стрелками взгляда или линиями разреза, получаем все необходимые виды и разрезы нашей детали. Но бывает иногда, когда мы разрезаем один из видов по центральной линии (линии симметрии например) мы не получаем нужный разрез. Компас его просто не создает. Самый простой выход из этой ситуации, и он чаще всего помогает: просто сместить линию разреза хотя бы на миллиметр, иногда можно и больше. Тогда разрез будет получен. Пусть он и будет не идеально точный, но глазу это не будет заметно и сгодится для оформления чертежа с простановкой всех размеров.
Основы проецирования
Проецированием называется процесс получения изображения предмета на плоскости.
Получившееся при этом изображение называют проекцией. Проекция – в переводе с латинского – «бросать (отбрасывать) вперёд».
В черчении изображения получают по так называемому методу проекций.
Чтобы построить изображение предмета по методу проекций, нужно через точки на предмете провести воображаемые лучи до встречи их с плоскостью. Эти лучи называются проецирующими. Плоскость, на которой получается изображение предмета, называется плоскостью проекций.
Если проецирующие лучи расходятся из одной точки, проецирование называется центральным (рис. 60а). Точка, из которой выходят лучи, называется центром проецирования.
Полученное при этом изображение называется центральной проекцией. Пример: тени, отброшенные от предмета лучами электрической лампочки.
Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным (рис. 60б), а полученное изображение – параллельной проекцией. Пример: солнечные тени.
При параллельном проецировании все лучи падают на плоскость проекций под одним и тем же углом. Если это любой острый угол, то проецирование называется косоугольным (рис. 61а). В косоугольной проекции, как и в центральной, форма и величина предмета искажаются.
Когда проецирующие лучи перпендикулярны к плоскости проекций, проецирование называют прямоугольным (рис. 61б), а полученное изображение – прямоугольной проекцией.
Способ прямоугольного проецирования является основным в черчении.
Проецирование на одну, две и три взаимно перпендикулярные плоскости проекций
Расположим предмет перед плоскостью проекций так, чтобы на получившемся изображении были видны три его стороны (рис. 62).
По такому изображению легко представить пространственный образ предмета.
Такое проецирование в черчении используют для построения наглядных изображений, однако, на наглядных изображениях предметы получают большие искажения и по ним трудно определить истинные размеры предмета.
Теперь расположим предмет перед плоскостью проекций так, чтобы на изображении была видна только одна его сторона, и построим его прямоугольную проекцию (рис. 63а).
На данном изображении проекции рёбер предмета, которые параллельны двум его измерениям (например: длина и ширина), равны натуральным размерам. Но на таком изображении нет третьего измерения предмета (высоты), поэтому оно не наглядно. Такие изображения используют в случаях, когда высота (толщина) детали одинакова во всех её точках (например, чертежи прокладок). Тогда на чертеже такой детали делают запись, указывающую её толщину (высоту). Пример приведен на рис. 63б (S4).
Иногда на одной плоскости изображают предметы, не имеющие одинаковой высоты во всех его точках. Тогда рядом с изображением точки числом указывают её высоту. Такие изображения называют проекциями с числовыми отметками (рис. 63в).
Чтобы судить о трёх измерениях предмета, его необходимо спроецировать ещё на одну плоскость проекций (П2), которая параллельна другой паре измерений предмета. Тогда вторая плоскость будет расположена перпендикулярно первой плоскости проекций (рис. 64).
Теперь по двум прямоугольным проекциям можно судить о размерах и форме предмета. Хотя форма не всегда ясно выражается двумя проекциями. Поэтому при изображении предметов сложной формы необходимо строить три (а иногда и более) прямоугольных проекции.
Возьмём три взаимно перпендикулярные плоскости проекций (рис. 65).
Одна из них занимает горизонтальное положение, её называют горизонтальной плоскостью проекций и обозначают П1. Две другие плоскости — вертикальные. Одну называют фронтальной плоскостью проекций (от французского слова «фронталь» – «лицом к зрителю»), другую – профильной плоскостью проекций (от французского слова «профиль» – «вид сбоку») и обозначают соответственно П2 и П3.
Линии пересечения плоскостей проекций называют осями проекций и обозначают буквами x, y, z. Точку пересечения осей проекций обозначают буквой О.
В трёхгранный угол, образованный плоскостями проекций, поместим параллелепипед и, проведя проецирующие лучи перпендикулярно плоскостям проекций, получим его проекции. Изображение на плоскости П1 – горизонтальная проекция, на плоскости П2 и П3 – соответственно фронтальная и профильная проекции.
Совмещённые плоскости с построенными на них изображениями предмета показаны на рис. 65б. Линии, соединяющие между собой проекции, называют линиями связи. Линии связи всегда перпендикулярны осям проекций.
На чертежах плоскости проекций не ограничивают и не обозначают. Кроме того, на чертеже при изображении предмета можно не наносить и оси проекций, так как при параллельном проецировании расстояние от плоскости проекций до изображаемого предмета не влияет на очертание его проекций (рис. 66а).
Это даёт возможность устанавливать произвольное расстояние между проекциями, сохраняя между ними проекционную связь даже при отсутствии линий связи (рис. 66б). Такой чертёж называется безосным. При построении проекций здесь пользуются осями симметрии предмета, центровыми линиями или характерными его плоскостями (рис. 67).
Метод прямоугольного проецирования на две и три взаимно перпендикулярные плоскости был разработан французским учёным-геометром Гаспаром Монжем в конце XVIII века. Поэтому его называют ещё методом Монжа.
Г. Монж положил начало развитию новой науки об изображении предметов – начертательной геометрии.
Способы построения третьей проекции
Проекционную связь между горизонтальной и профильной проекциями можно установить несколькими графическими приёмами:
На рис. 68а,б,в эти приёмы показаны на примере построения третьей проекции точки.
Удобнее всего пользоваться третьим способом, т.к. при наименьшем количестве графических операций достигается большая точность построения.
Если три вида уже построены, то место постоянной прямой чертежа произвольно выбирать нельзя. Нужно найти точку, через которую она пройдет. Для этого достаточно продолжить до взаимного пересечения горизонтальную и профильную проекции оси симметрии предмета. Через полученную точку К под углом 45° проводят отрезок прямой. Если осей симметрии на чертеже нет, то продолжают до пересечения в точке К1 горизонтальную и профильную проекции любой грани, проецирующейся в виде отрезков прямой (рис. 69).
Понятие связи в проекционном моделировании
Следующая тема, которую я хочу затронуть, — это объяснение, почему мы определили связь в конструкции как 4-Д объект. Напомню, что в проекционном моделировании связь – это общая часть элементов конструкта. Поскольку элементы конструкта – это 4-Д объекты, то связи – тоже 4-Д объекты. То есть, для существования связи между двумя 4-Д объектами должен быть общий 4-Д объем, принадлежащий обоим этим объектам.
Мы привыкли считать связью нечто, что существует между двумя объектами, но никто в аналитике еще не давал еще точного определения этому понятию. Мы сделали это впервые. Я расскажу, почему в данной дисциплине связь определена так, а не иначе.
Пространственные связи
Начнем с простого: пусть объекты связаны общим положением в пространстве или во времени. Это связи типа «справа», «выше», «после», «вместе» и т.д. Для моделирования такого рода связей нам нужно рассмотреть 4-Д пространство, в котором помещены рассматриваемые нами 4-Д объекты. 4-Д пространство играет такую же роль, как и другие 4-Д объекты. Обычно моделирование начинается именно с того, что мы формируем границы модели, то есть, 4-Д пространство, в котором потом размещаем 4-Д объекты. Почему-то про этот самый первый 4-Д объект забывают сразу после его определения. Но именно его свойства позволяют нам описать указанные мной связи.
В строительстве такого рода связи могут возникнуть, когда мы говорим, что крыша будет над зданием, а не под, или рядом. При проектировании процессов такого рода связи могут возникнуть, когда мы говорим, что данная операция следует за предыдущей. Все эти связи – это свойства 4-Д пространства, которое мы создали первым и в которое потом помещаем 4-Д объекты.
Взаимодействия
Второй тип связей – «поддерживает», «упирается», «передает усилие», то есть, все, что связано с силой. Сила возникает на границе двух тел в физике Ньютона, как результат взаимодействия полей в теории поля и как результат обмена частицами в квантовой механике.
Пусть одно тело давит на другое. Это значит, что между ними есть общая часть – граница. Эта граница принадлежит как первому, так и второму телу. Если же вы считаете, что это не так, то значит, между границами двух тел есть третье тело – среда, через которое передается взаимодействие (поле). И которое имеет общую часть как с первым телом, так и со вторым. Как бы то ни было – в модели взаимодействия всегда есть общие части будь то объектов или среды. Если же вы считаете, что поле – результат обмена частицами, то вы сами можете понять, что задача свелась к предыдущей.
Утверждение о том, что всегда есть нечто общее между взаимодействующими телами, — не результат анализа природных явлений, а результат анализа наших представлений о природе. Не надо путать реальность и ее модель. В нашем представлении нет способа передать взаимодействие напрямую без посредника. Поэтому любая связь – это 4-Д объект, передающий это взаимодействие. Но, повторюсь, не потому что так устроена природа, а потому что мы так мыслим.
Причинно-следственные связи
Еще один тип связи: когда объект, являясь результатом деятельности одной операции, затем используется в другой. Буквально это выглядит так: есть некий 4-Д объем, трактуемый нами как результат, который имеет общие части с первой и со второй операциями. Поскольку операция – это проекция 4-Д объема, то получается, что две операции имеют общий 4-Д объем, интерпретируемый нами как результат первой операции.
Потоки
Следующий тип связи – это потоки между функциями в функциональной структуре. Их можно увидеть в нотации IDEF0, моделируемых в виде стрелок между моделями функций. Почему IDEF0 моделирует функции и что такое функция, можно почитать здесь: Функция, сценарий и аппроксимация событий. Поскольку функция – это множество операций (событий), то для двух функций какие-то операции (события) могут стать общими. Например, пусть есть функция производства подшипников и функция потребления подшипников. Между ними мы обычно рисуем поток подшипников. Но давайте посмотрим на это более внимательно. В функции производства есть часть, отвечающая за отгрузку подшипников. А в функции потребления – часть, отвечающая за прием подшипников. Операции приема-передачи подшипников являются общими для обеих функций. С одной стороны, каждая такая операция трактуется как передача подшипника, а с другой – как прием подшипника. Но это один и тот же 4-Д объем! Кстати, если «склеить» все эти операции вместе, то получится функция «прием-передача подшипников», являющаяся частью функции производства подшипников и потребления.
Преимущества предлагаемого определения связи
Вся сила определения связи как 4-Д объема всплывает в кейсах, когда мы начинаем строить иерархические модели композиции и декомпозиции. Когда модели планарные, нет никакой разницы, как определять связь. Но, когда мы меняем точку зрения при переходе на более детальный, или более глобальный уровень, все становится не так очевидно.
Например, можно рассмотреть связь между производителем электроэнергии – ГЭС и потребителем – городом. Если связь 4-Д объект, то на этапе детализации можно «раскрыть» ее и показать, что это ЛЭП. Тогда связь «превратится» в ЛЭП. ЛЭП будет связана одной связью с ГЭС и другой – с городом. Дальнейшая детализация может «раскрыть» уже эти связи. Например, в городе будут выделены подстанции, а в ГЭС – открытый распределительный узел, ЛЭП будет представлена в виде двух цепей, а связь «раскроется» и превратится в вводы цепей. Обратное – тоже верно. Пусть есть множество связей между стыковочным модулем и космической станцией. При генерализации эти связи могут «генерализоваться» до одной связи.
В известных мне стандартах моделирования такого рода преобразования связей не предусмотрены. Есть намек в стандарте EPC, где операции связаны между собой общими событиями. Но «раскрыть» эти события нельзя. По замыслу автора нотации, эти события точно режут время на «до» и «после» операции. Однако, в свое время Что такое событие, или зачем четырехмерная геометрия бизнес-аналитику? я показал, что нет точного деления на «до» и «после». Операции часто «наваливаются» друг на друга, или наоборот, «разъезжаются» во времени. Это становится видно при детализации представления. Такого рода детализация невозможна в нотации EPC, но возможна в проекционном моделировании.