Что называют преобразованиями галилея
Физика Б1.Б8.
Электронное учебное пособие по разделу курса физики Механика
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
Введение
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.
Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).
Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.
Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.
Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.
Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.
Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.
Преобразования Галилея
Большинство встречающихся в повседневной жизни скоростей значительно меньше скорости света. Но существуют явления, где это не так (ядерная физика, электромагнетизм, фотоэффект, астрономия и т.д.).
Согласно представлениям классической механики, механические явления происходят одинаково в двух системах отсчета, движущихся равномерно и прямолинейно относительно друг друга.
Все ИСО (инерциальные системы отсчета) по своим механическим свойствам эквивалентны друг другу.
Это значит, что никакими механическими опытами, проводимыми внутри данной ИСО, нельзя установить, покоится эта система или движется равномерно и прямолинейно. Этот принцип является обобщением опыта и подтверждается всем многообразием приложений механики Ньютона к движению тел, скорости которых значительно меньше скорости света.
Все сказанное достаточно ясно свидетельствует об исключительности свойств ИСО, в силу чего именно эти системы должны, как правило, использоваться для изучения механических явлений.
Принцип относительности в классической механике
В проекциях на оси координат получим:
Чтобы получить формулы сложения скоростей в нерелятивистской механике, возьмем производную по времени:
Повторное дифференцирование приводит нас к равенству ускорений тела в любой ИСО:
Таким образом, ускорение точки в обеих системах отсчета одинаково. Говорят, что ускорение инвариантно относительно преобразований Галилея.
Сила в классической механике зависит от ускорения, которое она сообщает телу. Поэтому, как видно из преобразований Галилея, она не меняется при переходе от одной системы отсчета к другой. Отсюда следует, что уравнение, выражающее второй закон Ньютона, остается неизменным при переходе от одной ИСО к другой. Такие уравнения называются инвариантными. Таким образом, уравнения механики Ньютона инвариантны относительно преобразований Галилея. Это утверждение и составляет содержание принципа относительности Галилея. Равноправие ИСО дает возможность в каждом конкретном случае подбирать систему отсчета, наиболее удобную для решения рассматриваемой задачи.
Преобразования Галилея
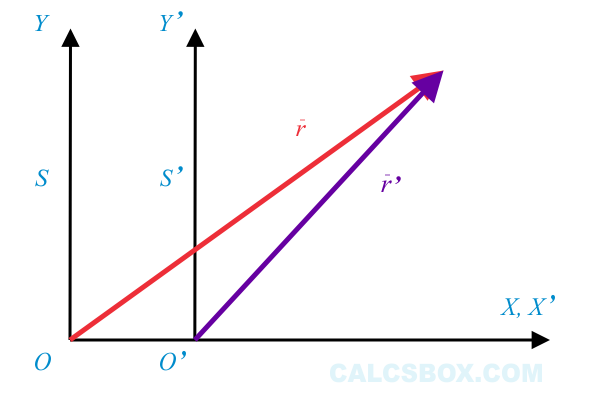
Преобразования Галилея позволяют переходить от одной системы отсчёта к другой.
Пусть дана система неподвижная отсчета и другая система отсчета, которая движится равномерно и прямолинейно относительно неподвижной системы отсчета.
Тогда расстояние, которое проходит тело в движушейся системе отсчета равно расстоянию, пройденному телом в неподвижной системе отсчета, за минусом произведения скорости на время для движущейся системы отсчета. Это преобразование Галилея.
Преобразования Галилея формула
В математическом виде преобразование Галилея:
Соотношение между скоростями
Соотношение между скоростями в неподвижной системе отсчета и в системе отсчета, которая движится равномерно и прямолинейно относительно неподвижной системы отсчета, таково:
где
vm – скорость тела в движущейся системе отсчета,
vn – скорость тела в неподвижной системе отсчета,
v – скорость движущейся системы отсчета.
Что касается ускорения, то они одинаковы в обеих данных системах отсчета.
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Принцип относительности Галилея.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: инерциальные системы отсчёта, принцип относительности Галилея.
Изучение теории относительности Эйнштейна мы начинаем с более глубокого рассмотрения принципа относительности Галилея. Это позволит нам лучше понять, каковы были предпосылки создания теории относительности.
Ключевую роль в механике и теории относительности играет понятие инерциальной системы отсчёта. Если вы забыли, что это такое, то обязательно прочитайте ещё раз Первый закон Ньютона.
В конце этой темы было кратко сказано о принципе относительности Галилея. Настало время поговорить о нём подробнее. В чём же суть данного принципа?
Наблюдатель на корабле.
Никаких отклонений обнаружить не удастся! Поставив в каюте корабля любой механический эксперимент и сопоставив его с аналогичным экспериментом на земле, вы увидите, что полученные результаты не отличаются друг от друга. Например, вы бросаете мячик со скоростью 5 м/с под углом к горизонту относительно палубы. Оказывается, мячик на корабле опишет ровно ту же самую траекторию, что и на берегу при тех же начальных условиях (скорость и угол броска).
Равномерное прямолинейное движение корабля никак не сказывается на протекании механических явлений на этом корабле. Поэтому никакой опыт из механики, проведённый в лаборатории корабля, не в состоянии определить, покоится ли корабль или движется равномерно и прямолинейно.
Систему отсчёта, связанную с землёй, во многих ситуациях можно считать инерциальной.(Конечно, Земля совершает суточное вращение и движется вокруг Солнца, поэтому земная лаборатория будет иметь ускорение. Но во многих задачах этим ускорением можно пренебречь.) Система отсчёта корабля, движущаяся относительно земной системы отсчёта равномерно и прямолинейно, также будет инерциальной. Мы приходим к выводу, что с точки зрения механических явлений инерциальные системы отсчёта совершенно равноправны: никакой механический эксперимент не в состоянии выделить и сделать привилегированной какую-то одну инерциальную систему отсчёта по сравнению с остальными.
Это и есть принцип относительности, открытый Галилеем.
Принцип относительности Галилея. Всякое механическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта.
Инвариантность законов механики.
Принцип относительности Галилея означает, что законы механики одинаковы во всех инерциальных системах отсчёта. А именно, математическая форма второго и третьего законов Ньютона не меняется при переходе от одной инерциальной системы отсчёта к другой. Давайте убедимся в этом непосредственно на следующем простом примере.
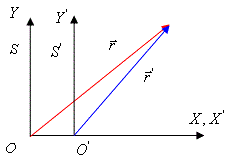
 |
| Рис. 1. Система движется относительно системы |
Прежде всего, выясним, как связаны друг другом координаты частицы и моменты времени в обеих системах отсчёта.
Таким образом, преобразования Галилея в механике служат математическим описанием перехода от одной инерциальной системы отсчёта к другой. Рассмотрим некоторые следствия, вытекающие из преобразований Галилея.
Три равенства (2) можно записать в виде одной векторной формулы:
Получился хорошо известный нам закон сложения скоростей: скорость тела относительно неподвижной системы отсчёта есть скорость тела относительно движущейся системы отсчёта плюс скорость движущейся системы относительно неподвижной. Мы видим, таким образом, что закон сложения скоростей в механике является следствием преобразований Галилея.
Итак,
ускорение частицы одинаково во всех инерциальных системах отсчёта. Это ещё одно следствие преобразований Галилея.
Теперь запишем второй закон Ньютона для нашей частицы в системе :
Силы в механике зависят от расстояний между телами и, быть может, скоростей тел друг относительно друга. Но расстояние между двумя точками пространства одинаково во всех инерциальных системах отсчёта. Скорость одной частицы относительно другой также не зависит от того, в какой инерциальной системе отсчёта рассматривается движение. Стало быть, сила одинакова во всех инерциальных системах отсчёта.
Величины и соотношения, не меняющиеся при определённых условиях, часто называются инвариантными. Так, ускорение, масса и сила инвариантны относительно выбора инерциальной системы отсчёта. Поэтому второй и третий законы Ньютона во всех системах отсчёта имеют одинаковый вид, т. е. инвариантны относительно преобразований Галилея.
Преобразования Галилея
Если в инерциальной системе K в точке с координатами x, y, z в момент времени t происходит некоторое событие, то представляется очевидным, что координаты и момент времени x’, y’, z’, t’ этого события в другой инерциальной системе K’, оси которой параллельны осям системы K, движущейся относительно K со скоростью V вдоль оси x, будут связаны с первыми формулами:
Формулы соответствуют случаю, когда в момент времени t = t ‘ = 0 начала координат обеих систем совпадают. Эти законы преобразования координат были названы преобразованиями Галилея.
Если вдоль оси x неподвижной системы движется вагон со скоростью V, а вдоль вагона в направлении его движения идет человек со скоростью v’ относительно вагона, то скорость человека относительно неподвижной системы будет равна v = v’ + V. Это настолько очевидный результат, что, кажется, не о чем и говорить. Однако это не так.
Координаты и моменты времени при переходе от одной инерциальной системы отсчета к другой преобразуются специальным образом. Следствием этих преобразований является закон сложения скоростей.
Пример преобразования Галилея:
В вагоне поезда, движущегося со скоростью V, со стола падает стакан. Пусть вагон — система K’, ось z’ расположена вертикально вверх, ось x’ — вдоль вагона в сторону движения. Стакан движется по закону:
В системе K, связанной с землей, стакан движется по закону: Материал с сайта http://worldofschool.ru
Траектория стакана в вагоне представляет собой вертикальную прямую, а относительно земли это парабола. Но закон природы не определяет траекторию. Согласно закону, определяющему движение стакана, в инерциальной системе ускорение a̅ = (0, 0, —g). Легко убедиться в том, что он имеет такой вид и в системе вагона, и в системе земли. Принцип относительности выполняется.
Преобразования Галилея. Принцип относительности в классической механике
Вы будете перенаправлены на Автор24
Все ИСО по своим механическим свойствам эквивалентны друг другу.
Это значит, что никакими механическими опытами, проводимыми внутри данной ИСО, нельзя установить, покоится эта система или движется равномерно и прямолинейно. Этот принцип является обобщением опыта и подтверждается всем многообразием приложений механики Ньютона к движению тел, скорости которых значительно меньше скорости света.
Все сказанное достаточно ясно свидетельствует об исключительности свойств ИСО, в силу чего именно эти системы должны, как правило, использоваться для изучения механических явлений.
Рисунок 1. Инерциальные системы отсчёта
В проекциях на оси координат получим:
Формулы обратного преобразования имеют вид:
Сила в классической механике зависит от ускорения, которое она сообщает телу. Поэтому, как видно из преобразований Галилея, она не меняется при переходе от одной системы отсчета к другой. Отсюда следует, что уравнение, выражающее второй закон Ньютона, остается неизменным при переходе от одной ИСО к другой. Такие уравнения называются инвариантными. Таким образом, уравнения механики Ньютона инвариантны относительно преобразований Галилея. Это утверждение и составляет содержание принципа относительности Галилея. Равноправие ИСО дает возможность в каждом конкретном случае подбирать систему отсчета, наиболее удобную для решения рассматриваемой задачи.
Движение происходит вдоль оси ОХ и соответственно закон преобразования (сложения) скоростей записывается через проекции скоростей на ось ОХ:
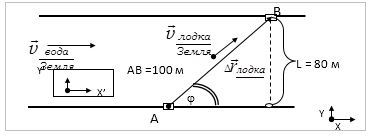
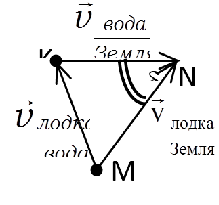
Лодка с мотором движется из точки А в точку В, которая находится на другом берегу реки (Рис. 3), скорость лодки относительно Земли неизменна по направлению. Расстояние АВ равно 100 м. Ширина реки равна 80 м. Скорость лодки относительно воды равна 1 м/с. Скорость воды в реке равна 1 м/с. Найти время переправы через реку.
Ответ: время переправы 83 с
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 11 2021