Что называют периодом функции

Периодическая функция

Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).

Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:

Число T называют периодом функции y=f(x).

Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).

Свойства периодических функций

1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).

2) Для любого x из области определения y=f(x) если T₁ — период функции, то

Так как T₂ также является периодом функции y=f(x), то для аргумента x-T₁

Следовательно, число T₁+T₂ является периодом функции y=f(x).

3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.

4) Если T — период функции f(x), то для аргумента kx+b

Значит число T/k — период функции f(kx+b).

5) Эти свойства следуют непосредственно из определения.

Например, для суммы f(x) и g(x):

Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.

Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.

Примеры периодических функций

1) Поскольку для любого x выполняются равенства

то функции y=sin x и y=cos x являются периодическими с периодом T=2π.

2) Так как для любого x из области определения функции y=tg x выполняется равенство

tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.

Аналогично, y=ctg x — периодическая функция с периодом T=π.

3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.

Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.

4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.

Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.

Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.

5) Так как для любого действительного x и любого целого k выполняется равенство =, то функция дробной части числа y= — периодическая с периодом T=k, где k∈Ζ, k≠0.

Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=.

Главный период функций y=sin x и y=cos x T=2π.

Главный период функций y=tg x и y=ctg x T=π.

Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.

То есть любой период функции y=sin x имеет вид 2πn, n∈Z.

Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.

Таким образом, 2π — главный период функции y=sin x.

Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.

Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период

а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период

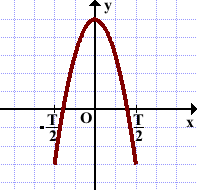
График периодической функции повторяется через промежутки длиной T (на оси Ox).

Дана часть графика

промежутке длиной T.

Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :

Источник

Периодические функции

С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

Дадим определение периодической функции:

Например, — периодические функции.

Для функций и период

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Источник