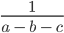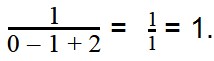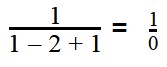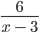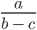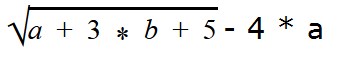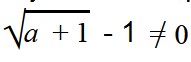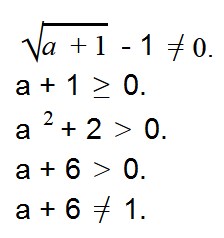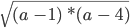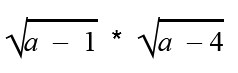Что называют переменной в алгебре 7 класс
Понятие и виды алгебраических выражений
п.1. Математические символы и выражения
В математическом языке мы используем особенные «слова», которые называются математическими выражениями, при этом «буквами» нам служат математические символы.
Список математических символов постоянно пополняется. Ведь при написании своей работы каждый вправе изобрести собственный иероглиф-символ, объяснить его смысл с помощью определения и предложить правила применения. Если символ окажется удачным и востребованным, то со временем он появится в других работах и начнёт самостоятельный путь по миру.
Допустим, по правилам, мы строим математические выражения, которые состоят из различных чисел (образованных цифрами, дробной чертой и десятичной запятой), знаков арифметических операций, возведения в рациональную степень, корней и скобок:
п.2. Определение и понятие переменной
Математические выражения с переменными также могут быть термами или формулами.
Если алгебраическое выражение не содержит деления на переменные и извлечения корня из переменных (или возведения переменных в степень с дробным показателем), то его называют целым выражением.
Примеры целых выражений:
Если алгебраическое выражение, кроме признаков целого выражения, содержит также деление на переменные, то его называют дробным выражением.
Примеры дробных выражений:
Целые и дробные выражения объединяют в класс рациональных выражений.
Если алгебраическое выражение содержит извлечение корня из переменных (или возведение переменных в степень с дробным показателем), то его называют иррациональным выражением.
Примеры иррациональных выражений:
п.4. Примеры
Значения выражений слева и справа действительно равны, формула истинна.
Ответ: формула истинна
Подставляем значения переменных:
Пример 4. Для проведения экзамена закупили k пачек бумаги по p рублей и m картриджей для принтера по q рублей. Напишите формулу, по которой можно найти общую сумму расходов S.
Значения выражений слева и справа действительно равны, формула истинна.
Что называют переменной в алгебре 7 класс
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: 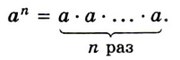
Степень числа а ≠ 0 с показателем 0 равна 1: а 0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
а m • а n = а m+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
(а m ) n = а mn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab) n = а n b n
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b) 2 = а 2 + 2аb + b 2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b) 2 = а 2 – 2аb + b 2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а 2 – b 2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а 3 + b 3 = (а + b)(a 2 – аb + b 2 )
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а 3 – b 3 = (а – b)(a 2 + ab + b 2 )
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 :
Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Алгебра 7 класс Все формулы
Уравнения
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы 
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
Алгебра 7 класс Все формулы
Функции
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Линейное уравнение с одной переменной
Содержание
Что такое уравнение
Для изучения темы линейного уравнения вспомним, что уравнением называют равенство, в составе которого есть неизвестное число. Это неизвестное число-переменную нам и нужно найти.
Чаще всего уравнения используют, чтобы решить задачу.
Приведем пример
Таким образом, записав по условию задачи уравнение, мы смоделировали алгебраическую модель ситуации.
Когда от нас требуется решить уравнение, мы должны найти все его корни либо показать, что их нет.
Корень уравнения – это значение неизвестной переменной, превращающее уравнение в верное равенство.
Рассмотрим пример
Корней может быть несколько, один или не быть совсем. В последнем случае говорят обычно, что уравнение не имеет решения или не имеет корней.
Что такое линейное уравнение
Подобные уравнения и называются линейными.
Иногда в составе уравнения есть несколько переменных, это тоже не наш случай: такие уравнения будут изучаться позже.
Коэффициенты и решение линейных уравнений
Посмотрим, когда линейное уравнение никак не может иметь корней (или верного решения).
Таким образом, при решении линейных уравнений мы пришли к трем общим ситуациям:
Свойства линейных уравнений
До того, как начать решать уравнение, над ним необходимо произвести все доступные арифметические действия, например, сложение/вычитание, раскрытие скобок, умножение/деление отдельно для свободных коэффициентов и отдельно для членов уравнения с неизвестной переменной.
Для упрощения дальнейшего решения с уравнениями можно произвести те же действия, что применяются к другим математическим выражениям.
Свойства линейных уравнений:
В процессе решения надо так преобразовать уравнение, чтобы все известные члены оказались с одной стороны равенства, а неизвестные – с другой.
Согласитесь, такое уравнение решить намного легче. При этом после подобных преобразований равенство не нарушается, и мы получаем равносильные уравнения.
Презентация по алгебре в 7 классе по теме » Выражения с переменными»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Выражения с переменными. Алгебра. 7 класс. Урок № 4. Аврамец Любовь Николаевна Струговска ООШ
Формула четного числа? Формула нечетного числа? Формула числа кратного 8? 10a+b, где a – цифра десятков, а b – цифра единиц Формула двузначного числа
7a a-5 a ≠ 5 МНОЖЕСТВО ВСЕХ ЧИСЕЛ, ПРИ КОТОРЫХ ВЫРАЖЕНИЕ С ПЕРЕМЕННОЙ ИМЕЕТ СМЫСЛ, НАЗЫВАЮТ МНОЖЕСТВОМ ДОПУСТИМЫХ ЗНАЧЕНИЙ ПЕРЕМЕННОЙ ИЛИ ОБЛАСТЬЮ ДОПУСТИМЫХ ЗНАЧЕНИЙ ПЕРЕМЕННОЙ.
3. Имеют ли смысл выражения?
Устно. 1. Вычислите значение выражения если 2. Найдите значение выражения М если если х = 2, у = 0,4
4. Известно, что при некоторых значениях a и b, a – b = 5. Какое значение имеет выражение: 2
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-735811
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Минпросвещения намерено расширить программу ускоренного обучения рабочим профессиям
Время чтения: 2 минуты
В Оренбурге школьников переведут на дистанционное обучение с 9 декабря
Время чтения: 1 минута
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Утверждено стратегическое направление цифровой трансформации образования
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Область допустимых значений функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 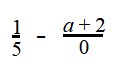
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.