Что называют осью абсцисс
Прямоугольная система координат
В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты». В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.
Координаты могут обозначаться самыми разными наборами цифр или букв.
Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого она города и кто ёё владелец.
Координаты — это набор данных, по которому определяется положение того или иного объекта.
Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте, запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.
Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или других символов, мы задаём координаты объекта.
Декартова система координат
Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.
Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.
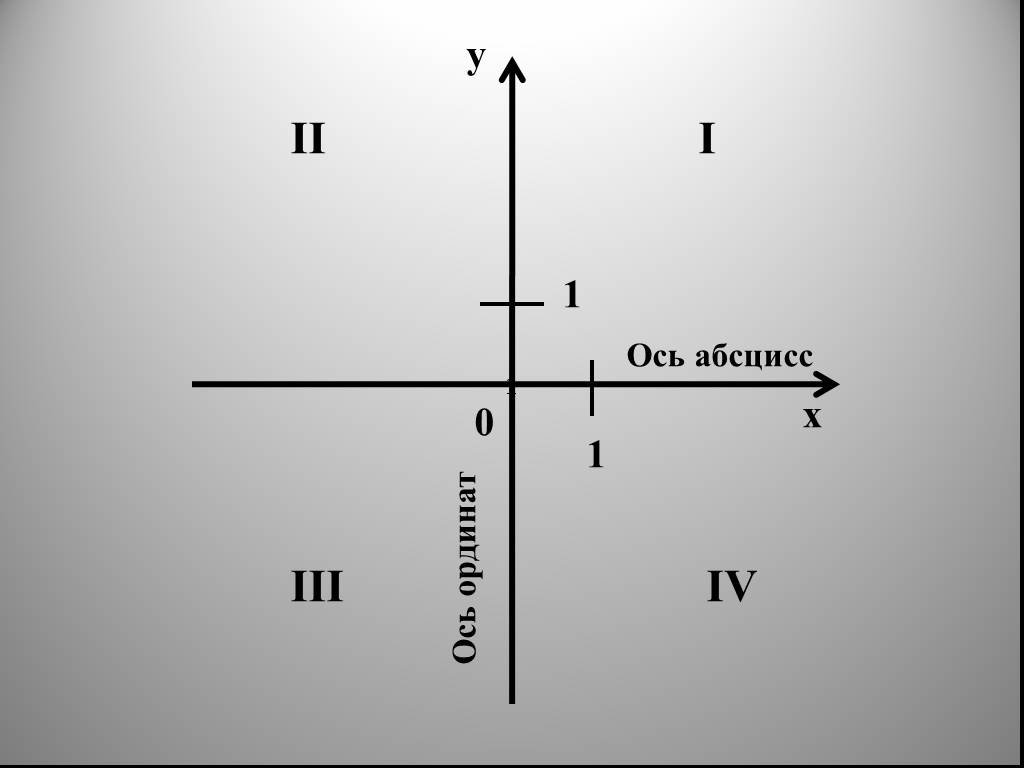
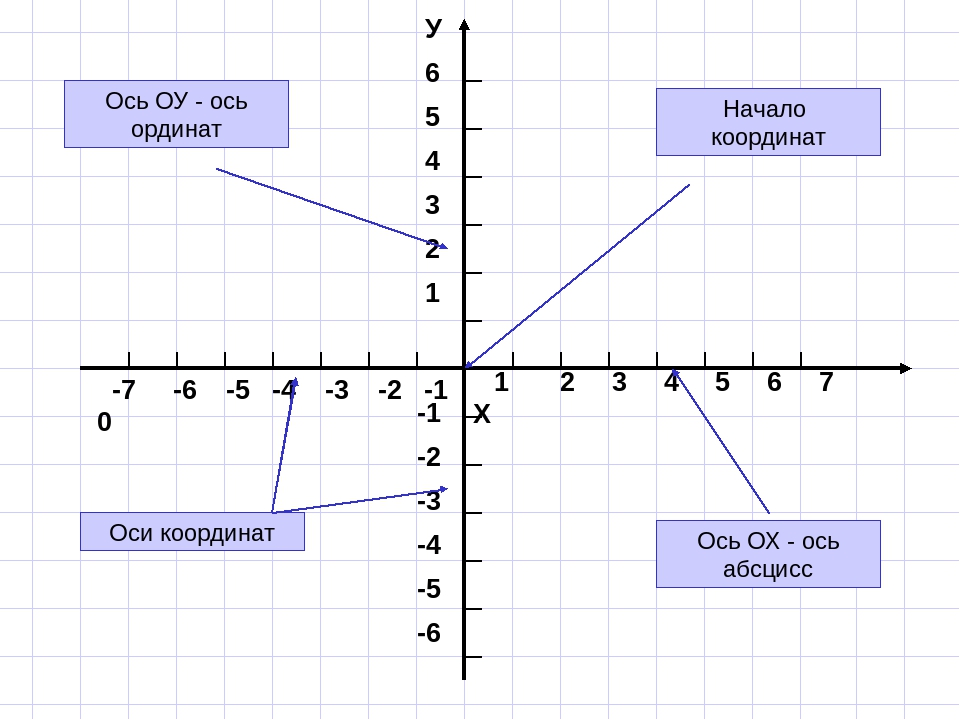
Оси взаимно перпендикулярны (т.е. угол между ними равен 90° ) и пересекаются в точке, которую обозначают « O ». Точка « O » является началом отсчёта для каждой из осей.
Система координат — это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них.
Координатные оси — это прямые, образующие систему координат.
Ось абсцисс « Ox » — горизонтальная ось.
Ось ординат « Oy » — вертикальная ось.
Координатная плоскость — плоскость, в которой построена система координат. Обозначается плоскость как « x0y ».
Обращаем ваше внимание на выбор длины единичных отрезков по осям.
Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева от оси « Oy ». Цифры на оси « Ox », как правило, пишут внизу под осью.
Обычно единичный отрезок на оси « 0y » равен единичному отрезку на оси « 0x ». Но бывают случаи, когда они не равны друг другу.
Отсчитываем четверти (или координатные углы) против часовой стрелки.
Значение слова «абсцисса»
[От лат. abscissa — отсеченная, отрезанная]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
В прямоугольной системе координат луч (прямая) X’X называется «осью абсцисс». При построении графиков функций, ось абсцисс обычно используется как область определения функции.
АБСЦИ’ССА, ы, ж. [латин. abscissa, букв. отрезанная] (мат.). Горизонтальный отрезок линии от точки пересечения координатных осей до ординаты искомой точки. На диаграмме роста сети железных дорог года нанесены на оси абсцисс.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
абсци́сса
1. матем. координата точки на оси X в прямоугольной системе координат ◆ Перемещение точки по абсциссе вызывает сдвиг проекции по ординате.
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова пифагорейцы (существительное):
Ось абсцисс

Всего получено оценок: 88.
Всего получено оценок: 88.
Оси абсцисс и ординат часто путают между собой. Это касается не только учеников, но и студентов и преподавателей нематематических дисциплин. Это знание ни на что особенно не влияет, но во многих теоремах пишут именно названия.
Системы координат
Название оси абсцисс относится к системам координат. На самом деле в мире используется две системы, хотя привычной для нас является декартова система координат.
Плоская декартова система координат состоит из двух взаимно перпендикулярных отрезков. Точка пересечения отрезков считается началом отчета. На каждом из отрезков обозначается единичный отрезок и направление движения.
Каждый из перпендикулярных отрезков называется осью. Единичный отрезок у каждой из осей может быть разным. Направления задаются, как правило, традиционно: вверх и вправо. Но иногда составители задач пытаются подловить учеников на этом и делают другие направления в системе. Поэтому, нужно быть крайне внимательным при работе с чужой системой координат.
Еще одной системой координат называется полярной. Если в декартовой системе для того, чтобы определить местоположение точки нужно знать две ее координаты, то в полярной системе нужно знать координату и угол подъема. Этой системой пользовались в древность, сегодня от нее почти отказались из-за излишней сложности.
Декартова система координат
Принцип работы с декартовой системой основан на понимании понятия проекции. Проекция в системе это перпендикуляр, опущенный на оси. Оси обозначаются как х и у. Ось х направлена вправо. Ось у направлена влево.
Представим себе точку на плоскости. Если нам нужно узнать ее координаты, то необходимо опустить два перпендикуляра: по одному на оси.
Так мы получим проекцию точки на ось х, это отрезок от начала отчета до точки пересечения оси с перпендикуляром. И проекцию отрезка на ось у: это расстояние на оси у от начала координат до точки пересечения оси с перпендикуляром.
Значение каждой из проекции и будет являться координатами точки на плоскости. По этим же координатам можно получить точку заново. Для этого нужно отложить требуемые значения на осях, после чего провести через отложенные точки прямые, перпендикулярные осям. Точка пересечения перпендикуляров и будет искомой прямой.
Оси декартовой системы
Вот мы и подошли к главному вопросу. Ось х имеет название оси абсцисс. Название это происходит от латинского «отрезок». Ось названа так потому, что отслеживает движение точки по горизонтали.
Вторая ось называется осью ординат, от латинского «порядок, движение по порядку». Имеется в виду, что эта координата отслеживает порядок движения вверх. Такая уж была логика у математиков древности.
Секрет в том, что названия осей можно менять как угодно, но оси все равно будут зваться осью абсцисс и осью ординат. Вне зависимости от буквенного обозначения осей, единичных отрезков и начала отсчета.
Что мы узнали?
Мы поговорили о системах координат. Выделили полярную и декартову систему. Отдельно обсудили декартову систему. Поговорили об обязательных характеристиках системы координат: единичный отрезок, направление осей, начало отсчета. Выяснили, что такое ось абсцисс. Поговорили о том, почему именно такое название получила каждая из осей.
Прямоугольная система координат. Ось абсцисс и ординат
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Прямоугольная декартова система координат
Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
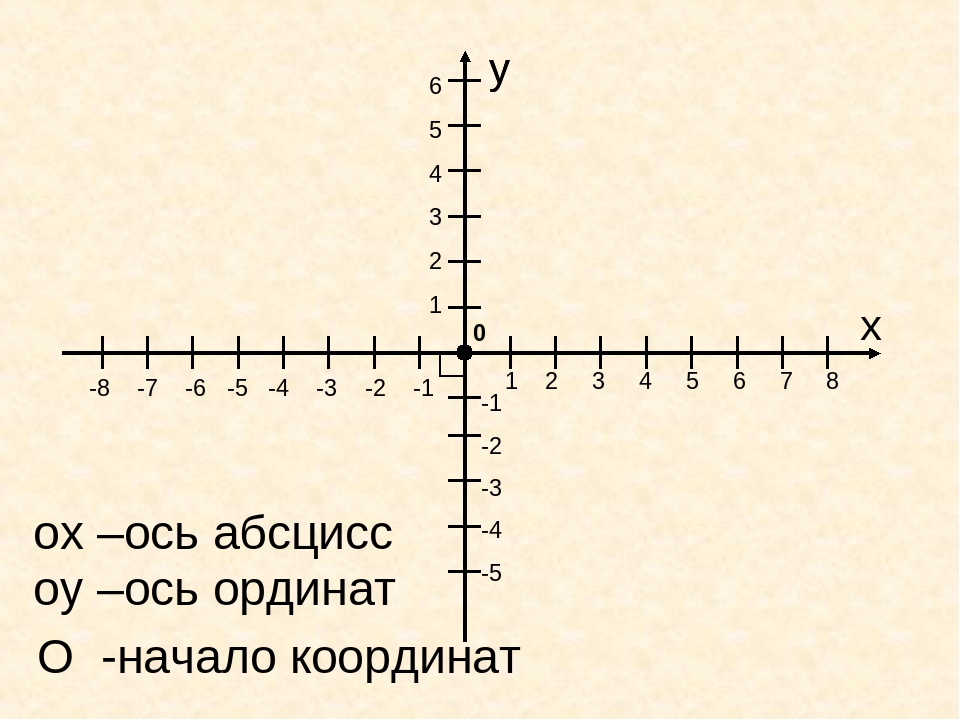
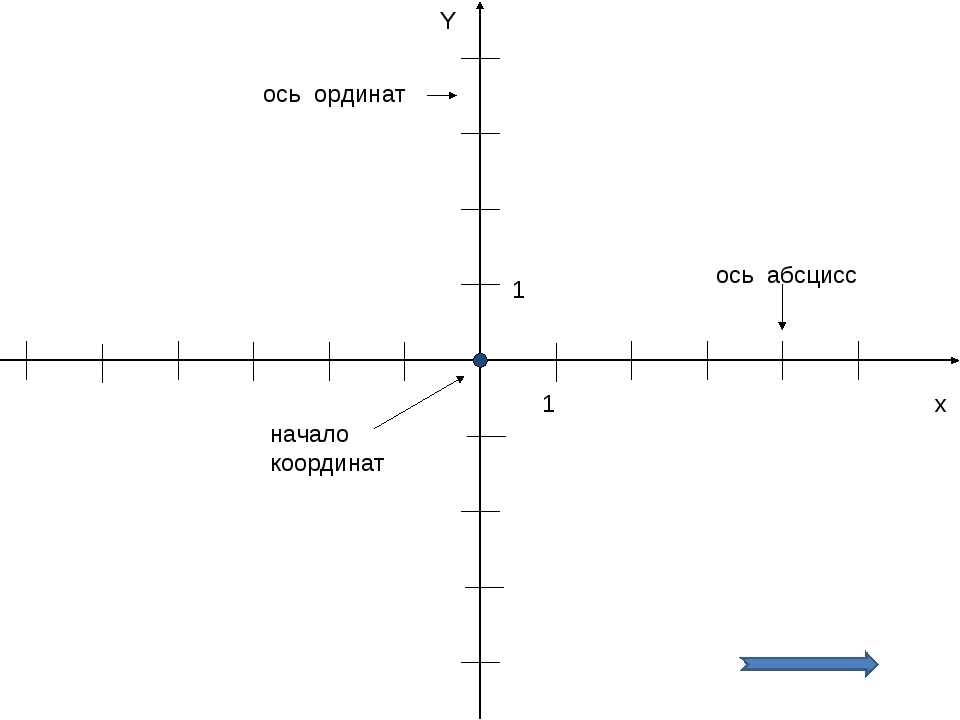
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
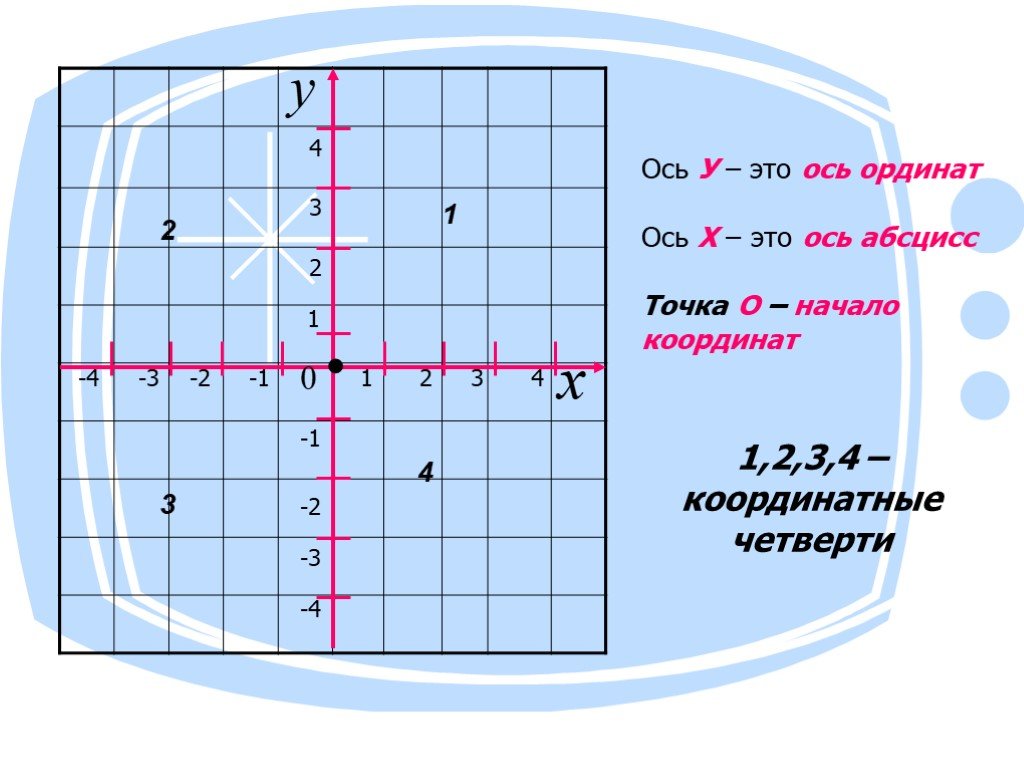
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
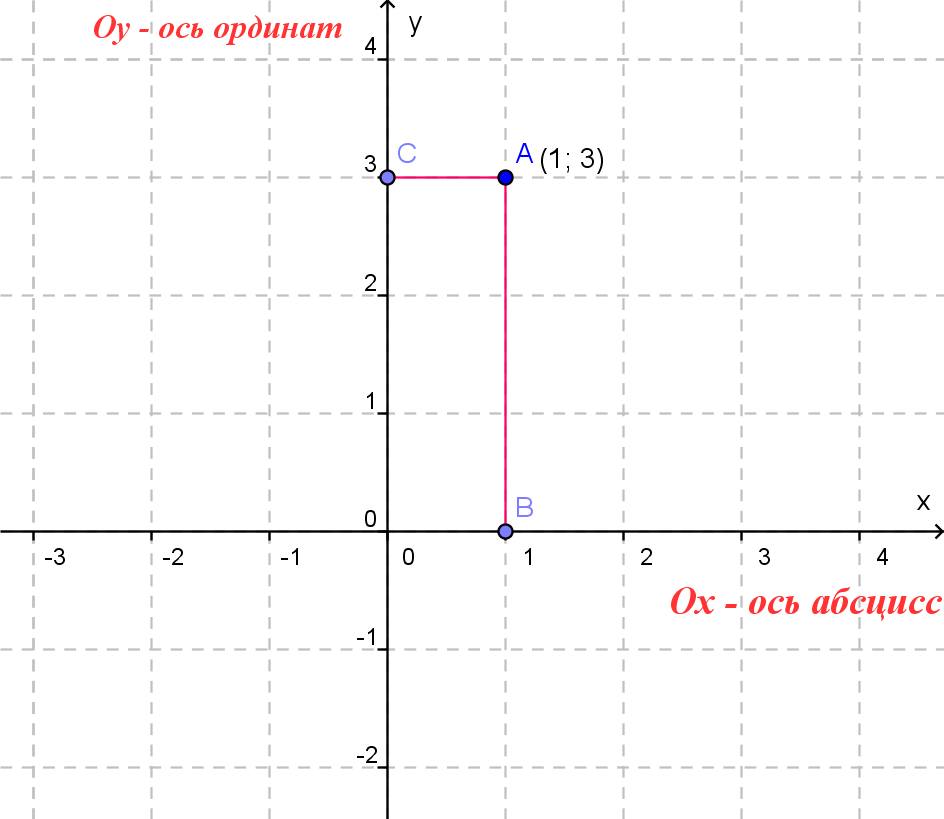
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
Прямоугольная система координат в трехмерном пространстве
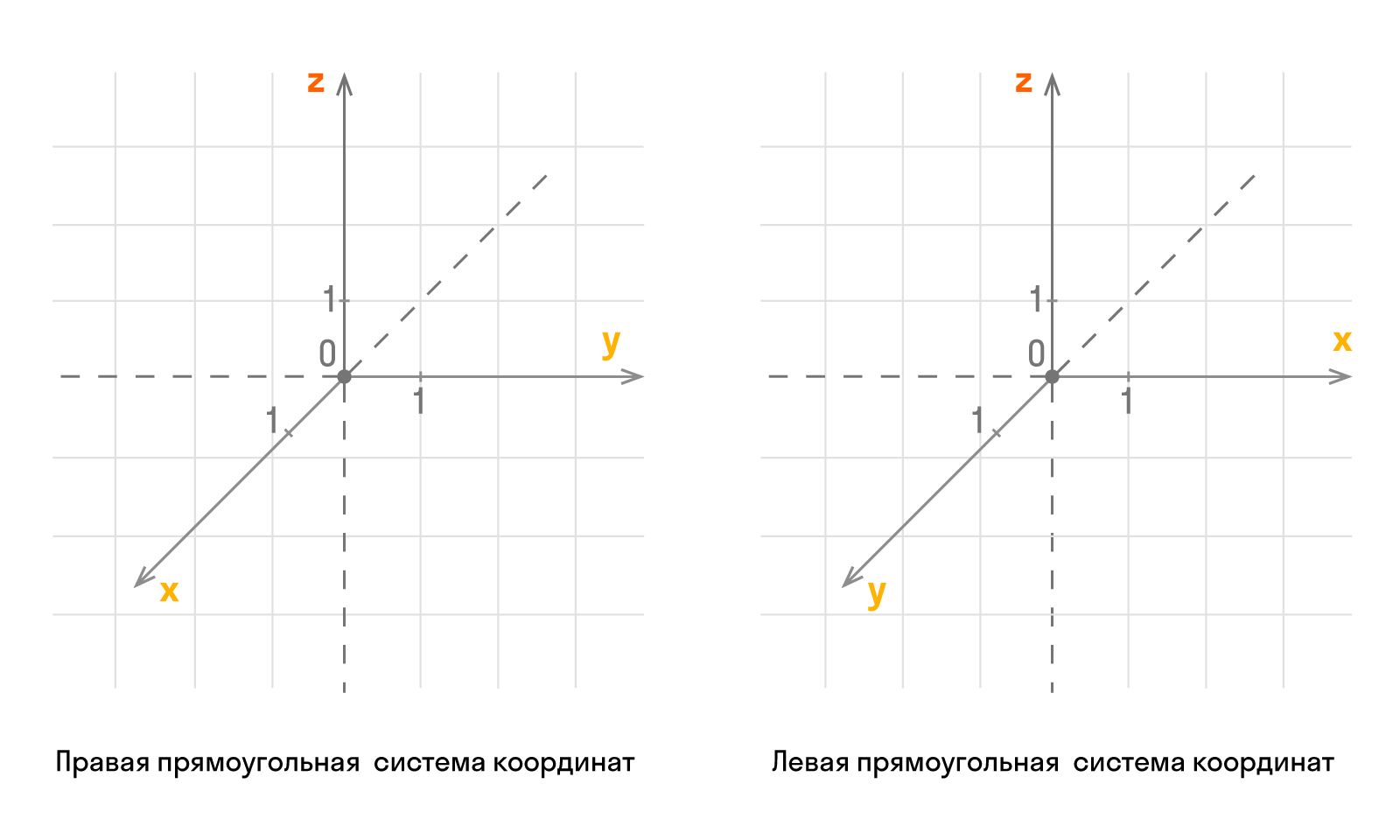
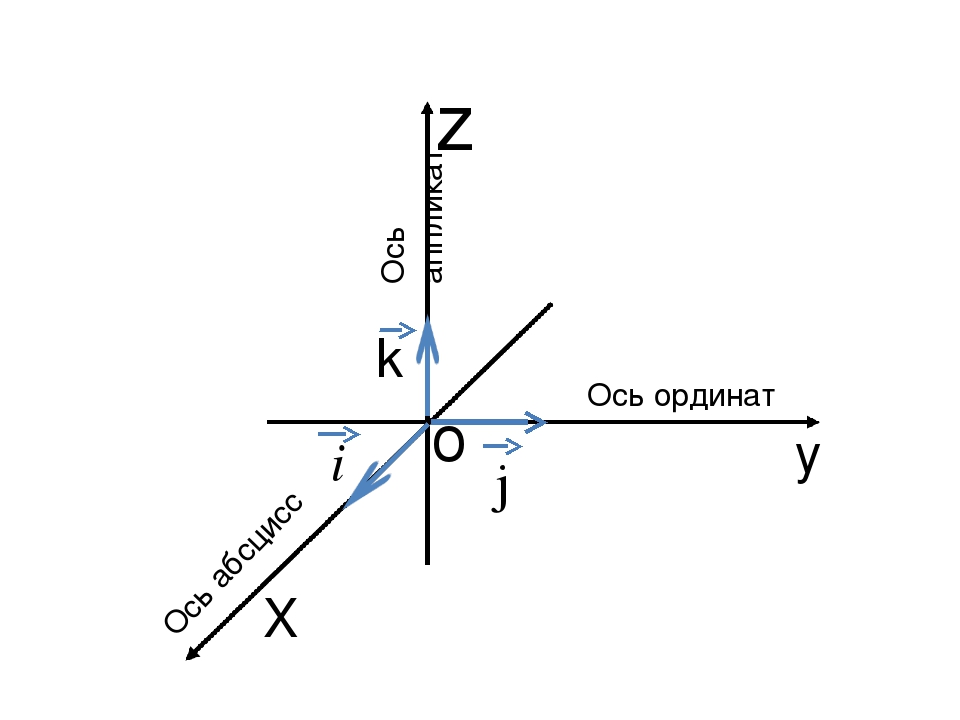
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.
Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.
Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Координаты точки в трехмерном пространстве
Сформулируем определение точки М в трехмерном пространстве.
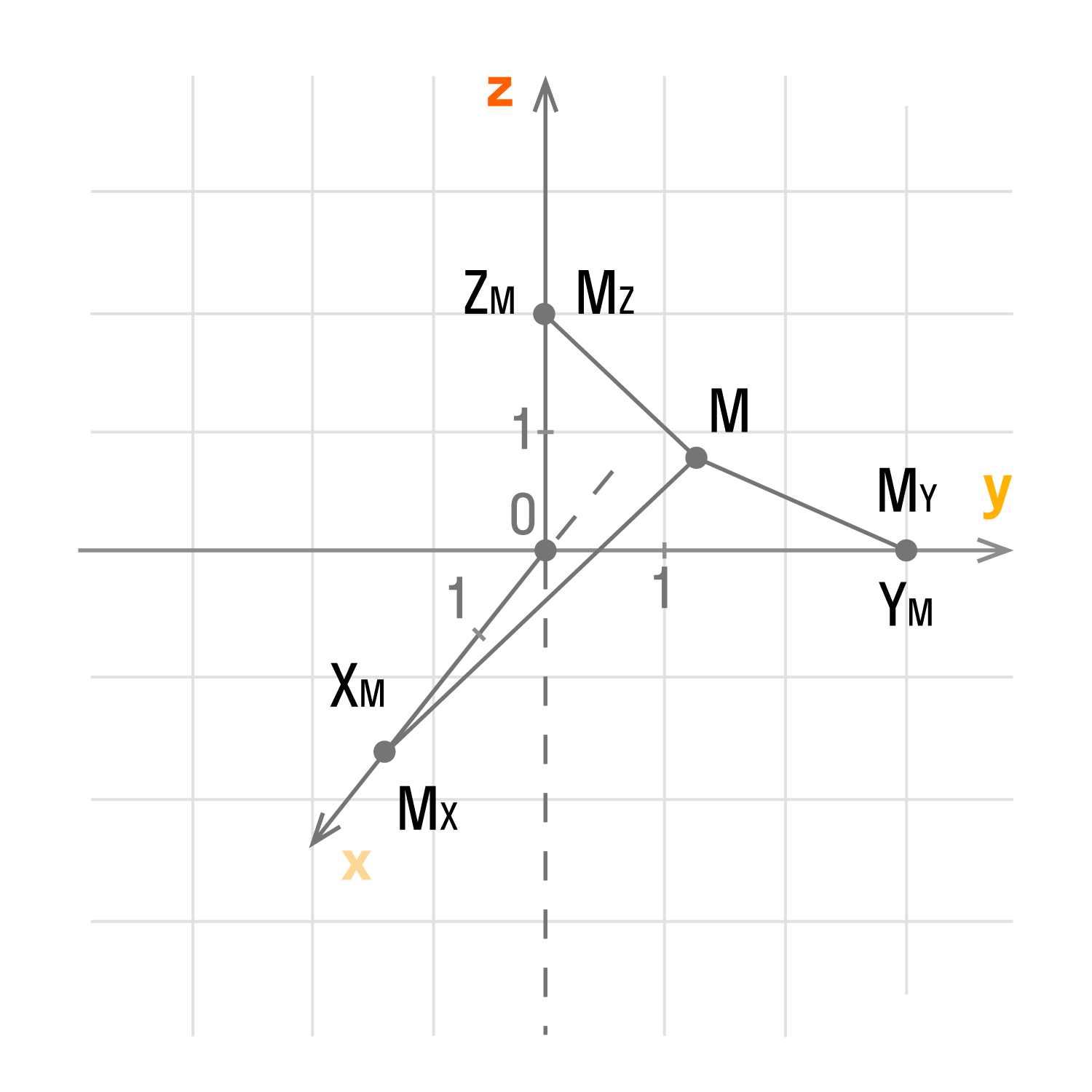
Пусть Mx, My, Mz — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения xM, yM, zM. Как это выглядит на координатных прямых:
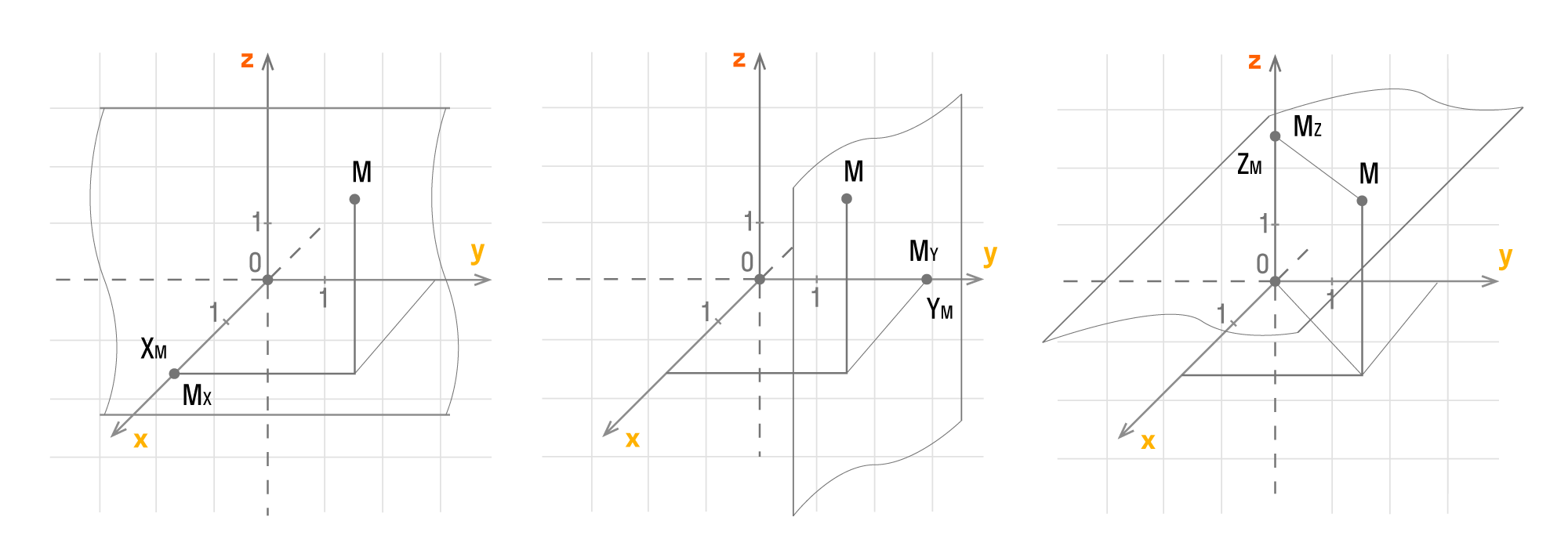
Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в Mx, My, Mz.
У каждой точки трехмерного пространства есть свои данные (xM, yM, zM), которые являются координатами точки М.
xM, yM, zM — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (xM, yM, zM) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.
Ось абсцисс
Системы координат
Название оси абсцисс относится к системам координат. На самом деле в мире используется две системы, хотя привычной для нас является декартова система координат.
Плоская декартова система координат состоит из двух взаимно перпендикулярных отрезков. Точка пересечения отрезков считается началом отчета. На каждом из отрезков обозначается единичный отрезок и направление движения.
Каждый из перпендикулярных отрезков называется осью. Единичный отрезок у каждой из осей может быть разным. Направления задаются, как правило, традиционно: вверх и вправо. Но иногда составители задач пытаются подловить учеников на этом и делают другие направления в системе. Поэтому, нужно быть крайне внимательным при работе с чужой системой координат.




Еще одной системой координат называется полярной. Если в декартовой системе для того, чтобы определить местоположение точки нужно знать две ее координаты, то в полярной системе нужно знать координату и угол подъема. Этой системой пользовались в древность, сегодня от нее почти отказались из-за излишней сложности.
Декартова система координат
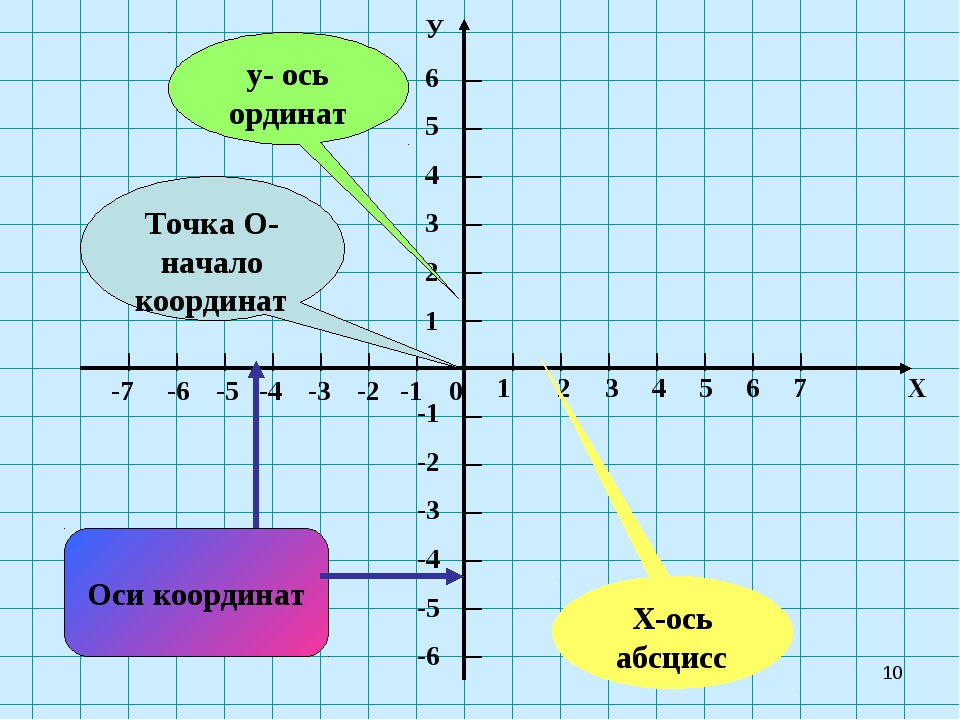
Принцип работы с декартовой системой основан на понимании понятия проекции. Проекция в системе это перпендикуляр, опущенный на оси. Оси обозначаются как х и у. Ось х направлена вправо. Ось у направлена влево.
Представим себе точку на плоскости. Если нам нужно узнать ее координаты, то необходимо опустить два перпендикуляра: по одному на оси.

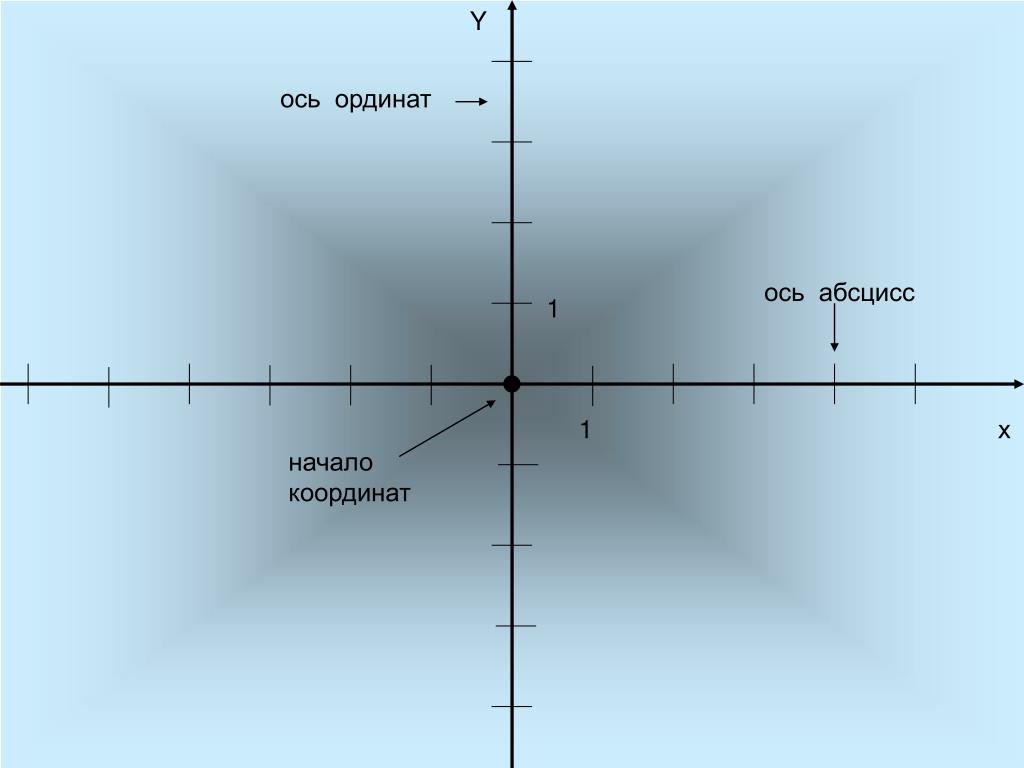

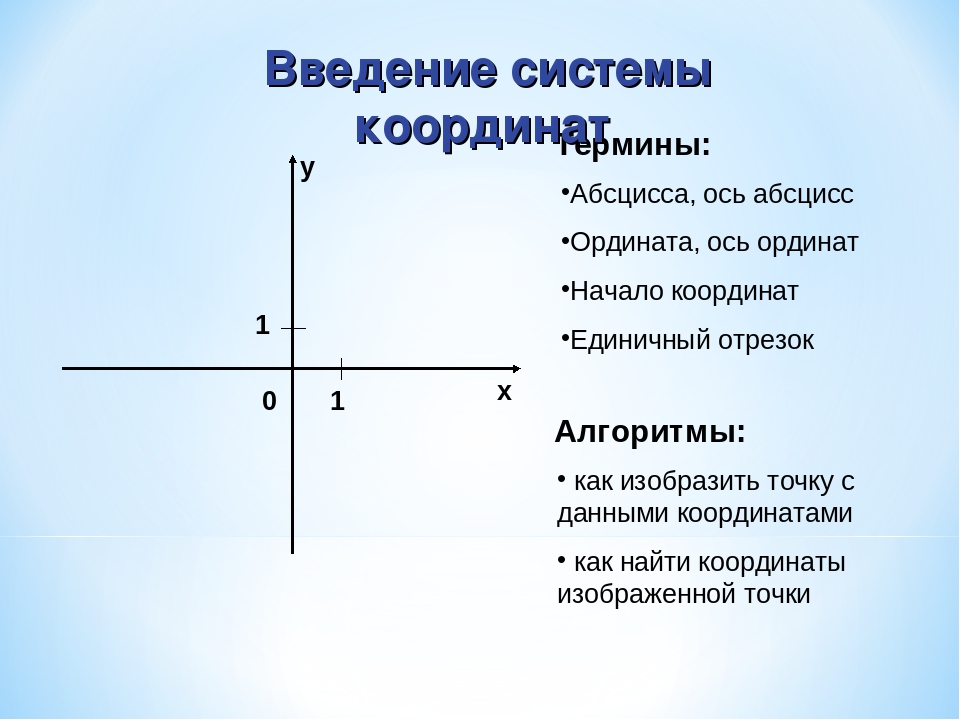



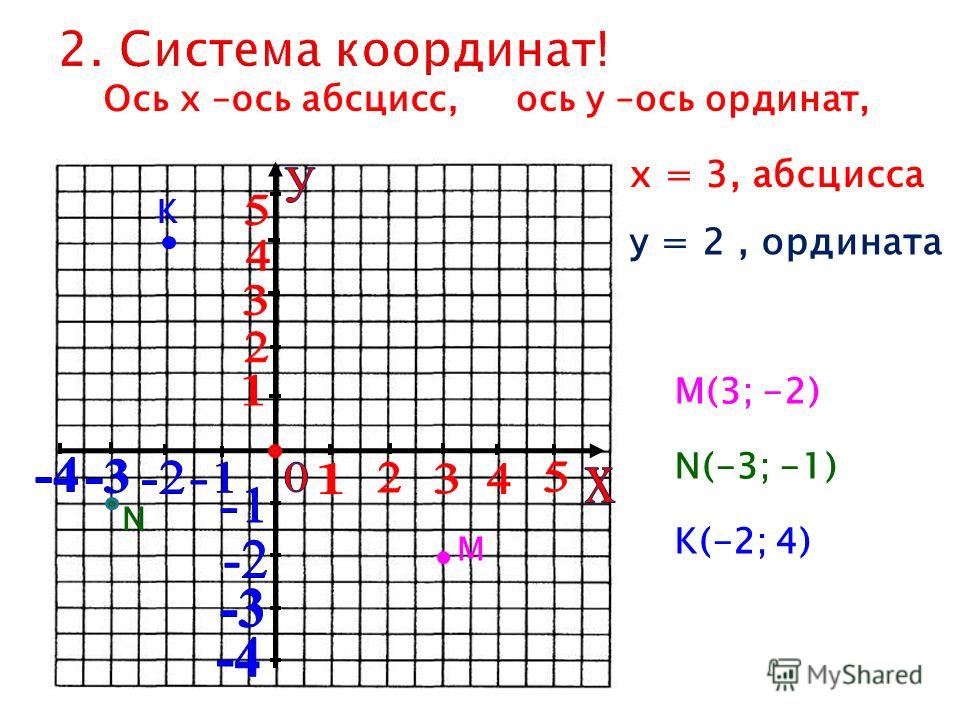
Так мы получим проекцию точки на ось х, это отрезок от начала отчета до точки пересечения оси с перпендикуляром. И проекцию отрезка на ось у: это расстояние на оси у от начала координат до точки пересечения оси с перпендикуляром.
Значение каждой из проекции и будет являться координатами точки на плоскости. По этим же координатам можно получить точку заново. Для этого нужно отложить требуемые значения на осях, после чего провести через отложенные точки прямые, перпендикулярные осям. Точка пересечения перпендикуляров и будет искомой прямой.
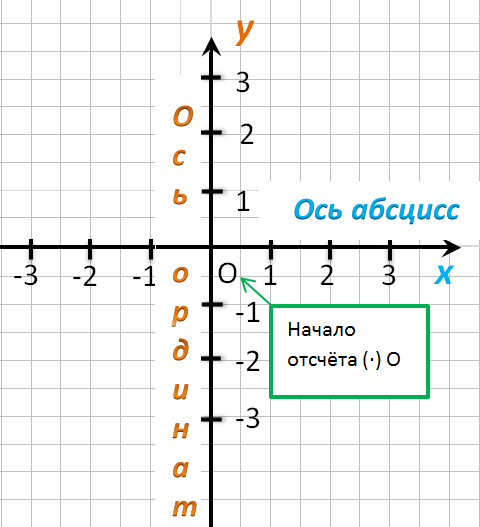
Оси декартовой системы
Вот мы и подошли к главному вопросу. Ось х имеет название оси абсцисс. Название это происходит от латинского «отрезок». Ось названа так потому, что отслеживает движение точки по горизонтали.







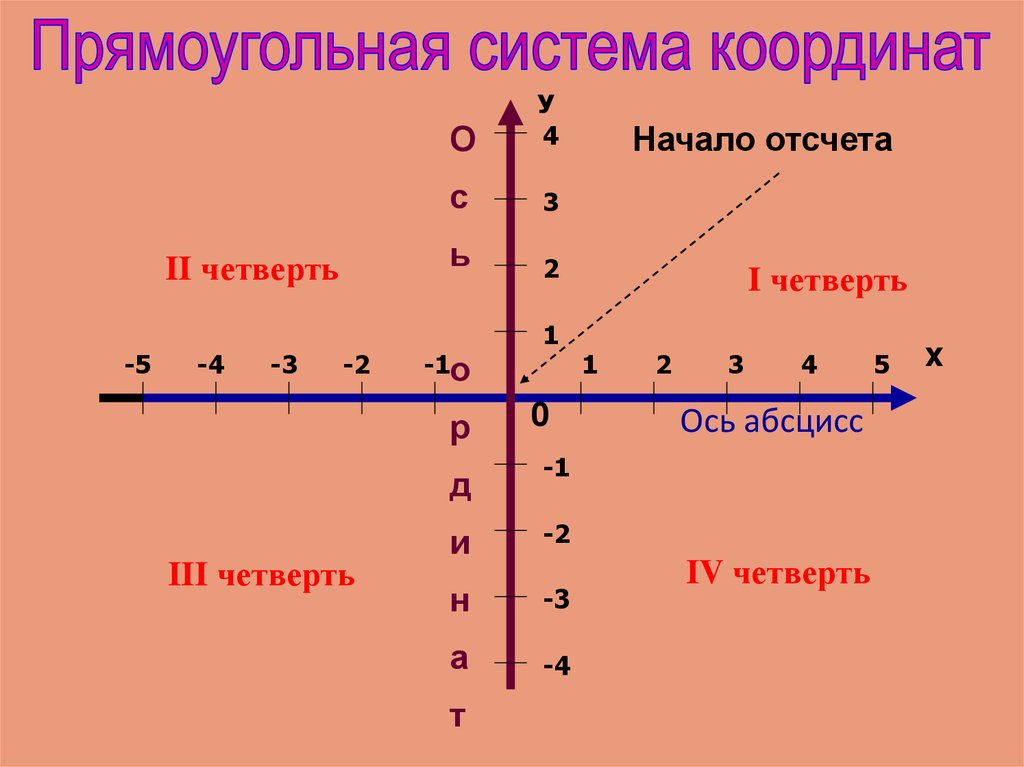
Вторая ось называется осью ординат, от латинского «порядок, движение по порядку». Имеется в виду, что эта координата отслеживает порядок движения вверх. Такая уж была логика у математиков древности.
Секрет в том, что названия осей можно менять как угодно, но оси все равно будут зваться осью абсцисс и осью ординат. Вне зависимости от буквенного обозначения осей, единичных отрезков и начала отсчета.
Что мы узнали?
Мы поговорили о системах координат. Выделили полярную и декартову систему. Отдельно обсудили декартову систему. Поговорили об обязательных характеристиках системы координат: единичный отрезок, направление осей, начало отсчета. Выяснили, что такое ось абсцисс. Поговорили о том, почему именно такое название получила каждая из осей.