Что называют основанием призмы

Призма. Виды призмы

Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.

Мы же поведем подробный разговор.

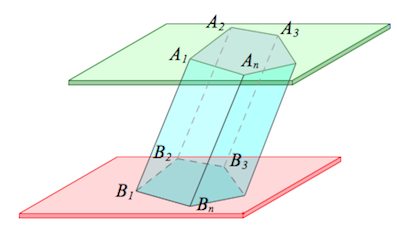
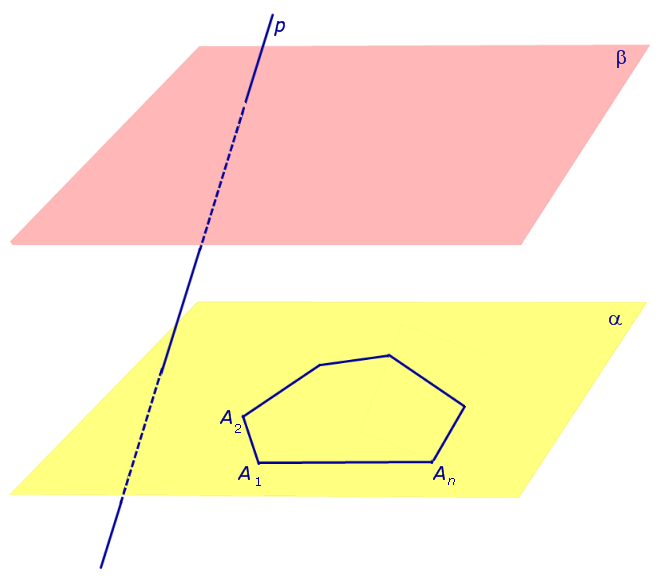
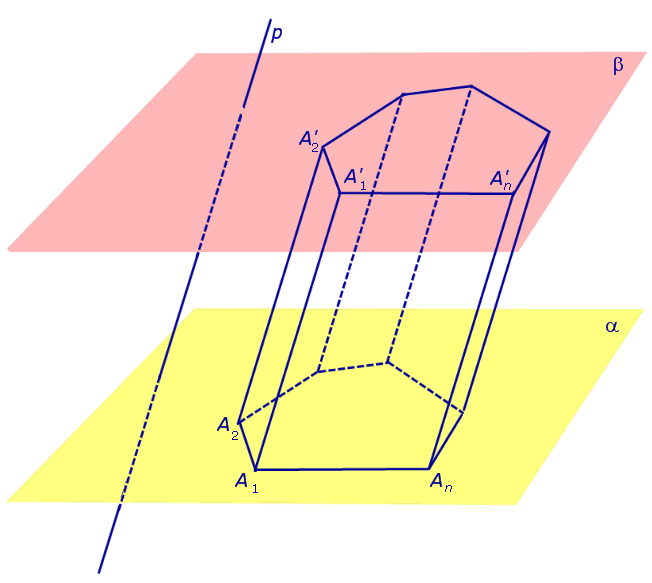
Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и параллелограммов .

Боковые грани – все грани, кроме оснований ( являются параллелограммами ).

Боковые ребра – общие стороны боковых граней ( параллельны между собой и равны ).

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

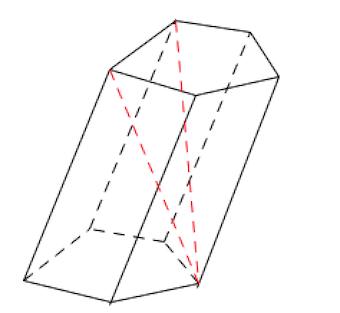
Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение –пересечение призмы и диагональной плоскости.

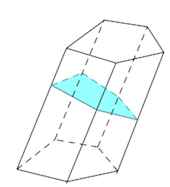
Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

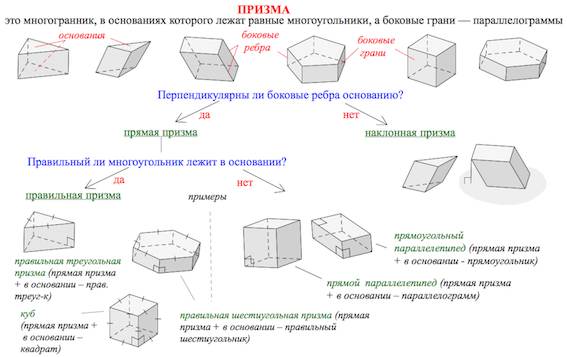
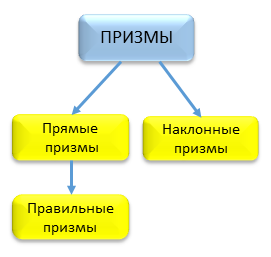
Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Параллелепипед – это призма, основаниями которой являются параллелограммы.

Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Частный случай прямоугольного параллелепипеда – куб.

Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике.

Смотрите также «Объем призмы. Площадь поверхности призмы».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

§ 1. Пространственные фигуры

1. Какие геометрические фигуры называются плоскими; пространственными?

Плоскими называются фигуры, точки которых принадлежат одной плоскости. Пространственными называются фигуры, точки которых принадлежат нескольким плоскостям.

2. Какое тело называют многогранником?

Многогранником называют тело, ограниченное плоскими многоугольниками.

3. Что называют гранями многогранника; рёбрами многогранника; вершинами многогранника?

Гранями многогранника называют плоскости, ограниченные сторонами многоугольников, из которых состоит многогранник.

Вершинами многогранника называют вершины многоугольников, из которых состоит многогранник.

Рёбрами многогранника называют стороны многоугольников, из которых состоит многогранник.

4. Какой многогранник называется призмой?

Призмой называется многогранник, две грани которого — равные n-угольники, а остальные n граней — параллелограммы.

5. Что называют основаниями призмы; боковыми гранями призмы; боковыми рёбрами призмы?

Основаниями призмы называют равные грани-многоугольники этой призмы.

Боковыми гранями призмы называют параллелограммы, из которых состоит призма.

Боковыми рёбрами призмы называют рёбра боковых граней, не принадлежащие основаниям.

6. Какая призма называется прямой призмой; наклонной призмой?

Прямой называется призма, боковые грани которой являются прямоугольниками.

Наклонной называется призма, боковые рёбра которой не перпендикулярны рёбрам основания призмы.

7. Какая призма называется правильной призмой?

Правильной называется прямая призма, основания которой являются правильными многоугольниками.

8. Какая призма называется параллелепипедом; прямым параллелепипедом?

Параллелепипедом называется призма, основаниями которой являются параллелограммы.

Прямым параллелепипедом называется параллелепипед, боковые грани которого являются прямоугольниками.

9. Какой прямой параллелепипед называется прямоугольным параллелепипедом?

Прямоугольным параллелепипедом называется прямой параллелепипед, основания которого являются прямоугольниками.

10. Какие рёбра прямоугольного параллелепипеда называются его измерениями?

Измерениями прямоугольного параллелепипеда называются рёбра, которые сходятся в одной вершине.

11. Какой многогранник называется пирамидой?

Пирамидой называется многогранник, одна грань которого — многоугольник, а остальные — треугольники с общей вершиной.

12. Что называют основанием пирамиды; боковыми гранями пирамиды; вершиной пирамиды?

Основанием пирамиды называют её многоугольную грань.

Боковыми гранями пирамиды называют её треугольные грани.

Вершиной пирамиды называют общую вершину её боковых граней.

13. Какая пирамида называется правильной пирамидой?

Правильной называется пирамида, основание которой — правильный многоугольник, а отрезок, соединяющий её вершину с центром основания, перпендикулярен любой прямой, проведённой в плоскости основания через этот центр.

14. Какой отрезок называется апофемой правильной пирамиды?

Апофемой правильной пирамиды называют высоту боковой грани пирамиды, опущенную из вершины пирамиды.

15. Сформулируйте свойство боковых рёбер правильной пирамиды; боковых граней правильной пирамиды; апофем правильной пирамиды.

16. Чему равна площадь боковой поверхности правильной пирамиды?

Площадь боковой поверхности правильной пирамиды равна произведению полупериметра её основания и апофемы.

17. Какое тело называется цилиндром?

Цилиндром называется тело, которое получено вращением прямоугольника вокруг одной из его сторон.

18. Какое тело называется конусом?

Конусом называется тело, которое получено вращением прямоугольного треугольника вокруг одного из его катетов.

19. Какое тело называется шаром?

Шаром называется тело, которое получено вращением круга вокруг своего диаметра.

20. Верно ли, что:

а) количество вершин любой призмы — число чётное.

Верно. Если дана призма с n-угольником в основании, то количество вершин равно n + n = 2n. А 2n делится на 2.

б) количество рёбер любой призмы — число, кратное трём?

Верно. Если дана призма с n-угольником в основании, то количество ребер будет равно сумме n ребер нижнего основания, n ребер верхнего основания и n боковых ребер. Таким образом, количество ребёр равно n + n + n = 3n. А 3n делится на 3.

21. Найдите количество диагоналей семиугольной призмы.

Из одной вершины можно провести n – 3 диагоналей. Количество диагоналей будет равно n × (n – 3) = 7 × (7 – 3) = 28.

22. Существует ли пирамида, которая имеет 11 рёбер? Обоснуйте свой ответ.

Такой пирамиды не существует, поскольку пирамида всегда имеет чётное количество рёбер, т.к. количество рёбер n-угольной пирамиды равно 2n, а 2n делится на 2.

Источник

Что такое призма: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение призмы

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.

На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.

Элементы призмы

Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

Варианты сечения призмы

Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.

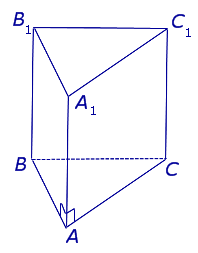
Виды призм

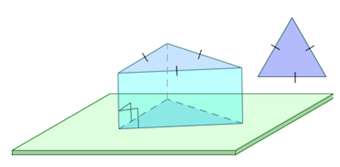
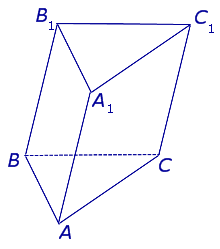
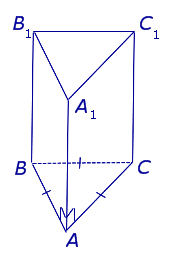
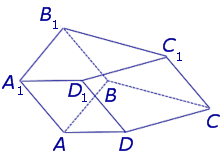
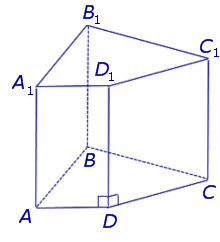
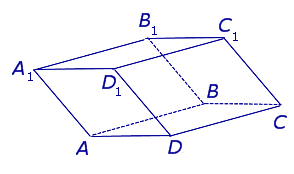
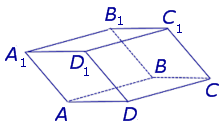
Рассмотрим разновидности фигуры с треугольным основанием.

Источник

Призмы

Основные определения и свойства призм. Теорема Эйлера

Утверждение 1. Каждый из n четырехугольников

Для остальных четырехугольников доказательство проводится аналогично.

Это утверждение непосредственно вытекает из утверждения 1.

Замечание 1. В случае, когда не требуется делать специальных уточнений,

боковые грани и основания призмы называют гранями призмы

совокупность всех граней призмы (всех боковых граней и оснований) называют полной поверхностью призмы,

n – угольные призмы называют призмами.

Доказательство. Заметим, что у n – угольной призмы 2n вершин, n боковых граней, 2 основания, 2n ребер основания и n боковых ребер. Следовательно, у n – угольной призмы (n + 2) грани и 3n ребер.

то теорема Эйлера доказана.

Замечание 2. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».

Замечание 3. С определением сечения призмы и способами построения сечений призмы ожно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».

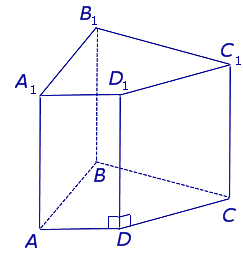
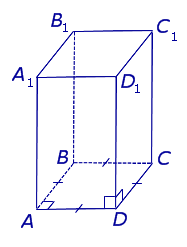
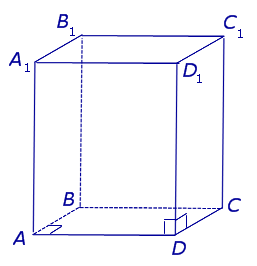
Виды призм. Прямые и наклонные призмы. Правильные призмы

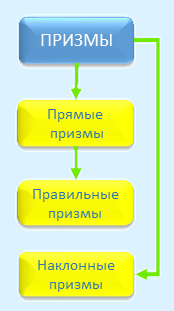
Существует следующая классификация призм.

Замечание 4. Все боковые грани прямой призмы являются прямоугольниками. Высота прямой призмы равна длине бокового ребра.

Определение 9. Правильной призмой называют прямую призму, основаниями которой служат правильные многоугольники.

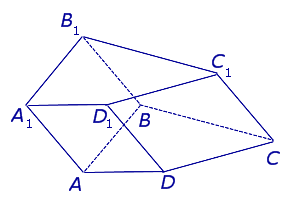
Определение 10. Диагональю призмы называют отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Примеры призм. Треугольные призмы. Четырехугольные призмы.
Параллелепипеды

ABС – произвольный треугольник.

ABС – произвольный треугольник.

ABСD – произвольный четырехугольник.

ABСD – произвольный четырехугольник.

Боковые грани правильной четырехугольной призмы – прямоугольники.

Противоположные грани параллелепипеда равны.

Все грани прямоугольного параллелепипеда являются прямоугольниками.

Правильный параллелепипед, у которого все грани равные квадраты.

У куба все ребра равны и попарно перпендикулярны.

Призма	Рисунок	Свойства
Наклонная треугольная призма
Правильная треугольная призма
Наклонная четырехугольная призма
Прямая четырехугольная призма
Правильная четырехугольная призма
Прямоугольный параллелепипед

Наклонная треугольная призма

ABС – произвольный треугольник.

Прямая треугольная призма

Правильная треугольная призма

ABСD – произвольный четырехугольник.

Правильная четырехугольная призма

Свойства:
Наклонная четырехугольная призма, все грани которой паралллелограммы.
Противоположные грани параллелепипеда равны.

Все грани прямоугольного параллелепипеда являются прямоугольниками.

Правильный параллелепипед

Куб

Свойства:
Правильный параллелепипед, у которого все грани равные квадраты.
У куба все ребра равны и попарно перпендикулярны.
Высота куба равна длине ребра.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Перечень вопросов, рассматриваемых в теме:

Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

Боковые грани – все грани, кроме оснований.

Боковые ребра – общие стороны боковых граней.

Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.

Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.

Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.

Площадь полной поверхности призмы – сумма площадей всех ее граней.

Площадь боковой поверхности призмы – сумма площадей ее боковых граней.

Параллелепипед – призма, все грани которой – параллелограммы.

Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,

геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.

Открытые электронные ресурсы:

Открытый банк заданий ФИПИ http://ege.fipi.ru/

Теоретический материал для самостоятельного изучения

Определение призмы. Элементы призмы.

Рассмотрим два равных многоугольника А₁А₂. А_n и В₁В₂. В_n, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А₁В₁, А₂В₂. А_nВ_n, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).

Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.

Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).

Рисунок 2 – Наклонная призма

Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.

Высота прямой призмы равна ее боковому ребру.

На рисунке 3 приведены примеры прямых призм

Рисунок 3 – Виды призм.

Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.

Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.

Площадь полной поверхности призмы. Площадь боковой поверхности призмы.

Площадью полной поверхности призмы (S_полн) называется сумма площадей всех ее граней, а площадью боковой поверхности (S_бок) призмы – сумма площадей ее боковых граней.

Таким образом, верно следующее равенство: S_полн= S_бок+2S_осн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.

Чему равна площадь боковой поверхности прямой призмы?

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом S_бок=P_оснh.

Пространственная теорема Пифагора

Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.

Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.

Рисунок 4 – Прямоугольный параллелепипед

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁ и найдем квадрат длины его диагонали А₁С.

Для этого рассмотрим треугольник А₁АС:

Ребро АА₁ перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА₁ перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА₁АС – прямоугольный.

По теореме Пифагора получаем: А₁С 2 =АА₁ 2 +АС 2 (1).

Так как в основании прямоугольник, то ВС=АD.

Что и требовалось доказать

Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.

Примеры и разбор решения заданий тренировочного модуля

Найдите для каждой картинки пару

1)2) 3)

4)5)

6)

Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.

Какие из перечисленных объектов могут быть элементами призмы?

1) параллельные плоскости

Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.

Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.

Источник