Что называют невозможной фигурой

Невозможные фигуры

Загадочные объекты и оптические иллюзии, один вид которых заставляет разум вскипать.

На первый взгляд кажется, что невозможные фигуры могут существовать только на плоскости. На самом деле невероятные фигуры могут воплощаться в трёхмерном пространстве, однако для «того самого эффекта» смотреть на них нужно с определённой точки.

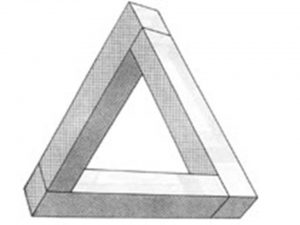
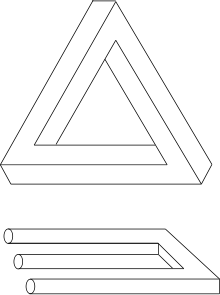
Вот, например, скульптура «невозможного треугольника» в Австралии: все его углы равны 90 градусам, чего с треугольниками в обычном мире не случается. Однако с другой точки скульптура выглядит таким образом.

Искажённая перспектива — частое явление в старинной живописи. Где-то это было обусловлено неумением художников выстраивать изображение, где-то — признаком равнодушия к реализму, которому предпочитали символизм. Материальный мир был отчасти реабилитирован в Возрождение. Мастера Ренессанса начали исследовать перспективу и открыли для себя игры с пространством.

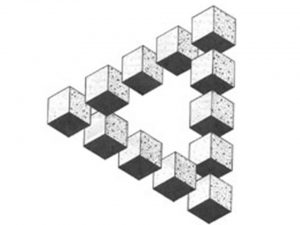
Большая слава пришла к невозможным фигурам ХХ веке. Шведский художник Оскар Рутесвард в 1934 году нарисовал составленный из кубов треугольник «Opus 1», а несколькими годами позже — «Opus 2B», в котором количество кубов уменьшилось. Сам художник отмечает, что самым ценным в разработке фигур, которую он предпринял ещё в школьные годы, следует считать не создание самих рисунков, а способность понять, что нарисованное парадоксально и противоречит законам евклидовой геометрии.

Моя первая невозможная фигура появилась случайно, когда я в 1934 году в последнем классе гимназии на уроке «чиркал» в учебнике латинской грамматики, рисуя в нем геометрические фигуры.

Ещё по этой теме :

В 50-х годах ХХ века вышла статья британского математика Роджера Пенроуза, посвящённая особенностям восприятия пространственных форм, изображённых на плоскости. Статья была опубликована в «Британском журнале психологии», что многое говорит о сущности невозможных фигур. Главное в них — даже не парадоксальная геометрия, а то, как наш разум воспринимает такие явления. Как правило, требуется несколько секунд, чтобы понять, что именно «не так» не так с фигурой.

Благодаря Рождеру Пенроузу на эти фигуры взглянули с точки зрения науки, как на объекты с особыми топологическими характеристиками. Австралийская скульптура, речь о которой шла выше, представляет собой как раз невозможный треугольник Пенроуза, в котором все составляющие реальны, однако в целостность, которая может существовать в трёхмерном мире, картинка не складывается. Треугольник Пенроуза вводит в заблуждение с помощью ложной перспективы.

Загадочные фигуры стали источником вдохновения и для физиков с математиками, и для художников. Вдохновившись статьёй Пенроуза, график Мауриц Эшер создал несколько литографий, которые принесли ему известность художника-иллюзиониста, и впоследствии продолжил экспериментировать с пространственными искажениями на плоскости.

В ХХ веке философия, живопись, литература обратились к уникальным и неповторимым переживаниям субъекта. Главным предметом интереса стали не действия и явления как таковые, а их восприятие, отражение в сознании. Неудивительно, что невозможная геометрия, которая прежде воспринималась как ошибка или курьёз, теперь стала самостоятельным художественным методом.

Вот ещё несколько известных фигур-парадоксов, которые до сих пор продолжают расшатывать разум зрителей.

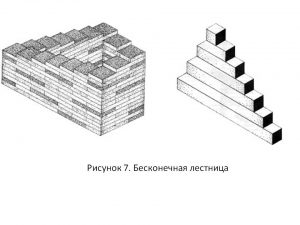
Бесконечная лестница

Модель фигуры была разработана Рождером Пенроузом и его отцом Лайонелом Пенроузом. Изображённая ими лестница делает поворот на 90 градусов и замыкается, так то человек, если бы ему вздумалось по ней взойти, не смог бы подняться выше. На рисунке ниже видно, что собака и человек стоят на одном уровне, что тоже добавляет рисунку невозможности. Если персонажи пойдут по часовой стрелке, то будут постоянно спускаться, а если против часовой — подниматься.

Ранее такую лестницу изображал Оскар Рутесвард, о чём Пенроузы не знали, а Мауриц Эшер популяризировал образ «сумасшедшей лестницы» в искусстве, создав знаменитую работу «Относительность».

Невозможная вилка

Невозможный трезубец, бливет или даже, как его ещё называют, «вилка дьявола», представляет собой фигуру с тремя круглыми зубцами на одном конце и прямоугольными — на другом. Выходит, что объект вполне нормален в правой и левой части, а вот в комплексе получается форменное безумие.

Такой эффект достигается за счет того, что трудно однозначно сказать, где тут передний план, а где задний.

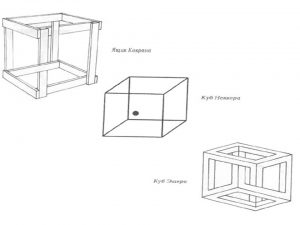
Иррациональный куб

Невозможный куб (он же — «куб Эшера») появился на литографии Маурица Эшера «Бельведер». Кажется, что самим существованием этот куб нарушает все основные геометрические законы. Разгадка, как и всегда с невозможными фигурами, довольно проста: человеческому глазу свойственно воспринимать двумерные изображения как трёхмерные объекты.

Читайте также :

Между тем, в трёх измерениях невозможный куб выглядел бы таким образом и с определённой точки казался бы таким же, как рисунок выше.

Невозможные фигуры представляют большой интерес для психологов, когнитивистов и эволюционных биологов, помогая больше узнать о нашем зрении и пространственном мышлении. Сегодня компьютерные технологии, виртуальная реальность и проекции расширяют возможности, так что на противоречивые объекты можно взглянуть с новым интересом.

Кроме классических примеров, которые мы привели, существует множество других вариантов невозможных фигур, а художники и математики придумывают всё новые парадоксальные варианты. Скульпторы и архитекторы используют решения, которые могут показаться невероятными, хотя их вид зависит от направления взгляда зрителя (как Эшер и обещал — относительность!).

Чтобы попробовать себя в создании объёмных невозможностей, профессиональным архитектором быть не обязательно. Существуют оригами невозможных фигур — такое можно повторить дома, скачав заготовку.

Источник

Невозможные фигуры

Цель проекта:

1.Выяснить, как создаются невозможные фигуры и где их применяют.

Задачи проекта:

1.Изучить литературу по теме «Невозможные фигуры».

2.Составить классификацию невозможных фигур.

Тема работы актуальна ведь понимание парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Многие работы с нереальными объектами можно отнести к «интеллектуальным математическим играм». Моделировать подобный мир можно только с помощью математических формул, человек представить его просто не в состоянии. И для развития пространственного воображения оказываются полезными невозможные фигуры. Человек неустанно мысленно создает вокруг себя то, что для него будет просто и понятно. Он даже не может себе представить, что некоторые объекты, окружающие его, могут быть «невозможными». На самом деле мир един, но рассматривать его можно с разных сторон.

1.Определение невозможных фигур

Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры[1].

Невозможные фигуры – это геометрически противоречивые изображения объектов, не существующих в реальном трёхмерном пространстве. Невозможность возникает из противоречия между подсознательно воспринимаемой геометрией изображённого пространства и формально-математической геометрией.

Невозможные фигуры разделяются на два больших класса: одни имеют реальные трехмерные модели, а для других такие создать невозможно.

Невозможные фигуры достаточно часто встречаются на древних гравюрах, картинах и иконах — в одних случаях мы имеем с явными ошибками передачи перспективы, в других — с умышленными искажениями, обусловленными художественным замыслом.

В средневековой японской и персидской живописи невозможные объекты являются неотъемлемой частью восточного художественного стиля, дающего лишь общий набросок картины, детали которой «приходится» додумывать зрителю самостоятельно, в соответствии со своими предпочтениями [2].

Картины с искаженной перспективой встречаются уже в начале первого тысячелетия. На миниатюре из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене, нарисована «Мадонна с младенцем» (рис.1). На картине изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект нереальности.

Рисунок 1. «Мадонна с младенцем»

2.Виды невозможных фигур

Эта – фигура – возможно первый опубликованный в печати невозможный объект. Она появилась в 1958 году. Её авторы, отец и сын Лайонелл и Роджер Пенроузы, генетик и математик соответственно, определили этот объект как «трехмерную прямоугольную структуру»[2]. Она также получила название «трибар». С первого взгляда трибар кажется просто изображением равностороннего треугольника. Но стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В тоже время левая и правая грани внизу тоже кажутся перпендикулярными. Если смотреть на каждую деталь отдельно, то она кажется реальной, но, в общем, эта фигура существовать не может. Она не деформирована, но при черчении были неправильно соединены правильные элементы.

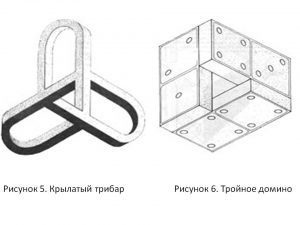
Вот еще несколько примеров невозможных фигур на основе трибара (рис.3-6).

Рисунок 3. Тройной деформированный трибар

Рисунок 4. Треугольник из 12 кубов

фигуру чаще всего называют «Вечной лестницей» или «Лестницей Пенроуза» – по имени ее создателя. Ее также называют «непрерывно восходящей и нисходящей тропой»

Впервые эта фигура была опубликована в 1958 году [2]. Перед нами предстает лестница, ведущая, казалось бы, вверх или вниз, но при этом, человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути.

«Бесконечной лестницей» с успехом воспользовался художник Мауриц К. Эшер, на этот раз в своей литографии «Восхождение и нисхождение», созданной в 1960 году.

Лестница с четырьмя или семью ступеньками. На создание этой фигуры с большим количеством ступенек автора могла вдохновить куча обыкновенных железнодорожных шпал. Собравшись взобраться на эту лестницу, вы будете стоять перед выбором: подняться ли по четырем или по семи ступенькам.

Следующая группа фигур под общим названием «Космическая вилка». С этой фигурой мы входим в самую сердцевину и суть невозможного. Может быть, это самый многочисленный класс невозможных объектов (рис.8).

Рисунок 8. Космическая вилка

Этот пресловутый невозможный объект с тремя (или с двумя?) зубцами стал популярен у инженеров и любителей головоломок в 1964 году. Первая публикация, посвященная необычной фигуре, появилась в декабре 1964 года. Автор назвал ее «Скобой, состоящей из трех элементов».

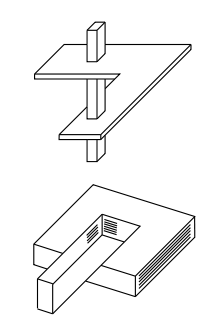
Еще один невозможный объект появился в 1966 году в Чикаго в результате оригинальных экспериментов фотографа доктора Чарльза Ф. Кокрана. Многие любители невозможных фигур проводили эксперименты с «Сумасшедшим ящиком». Первоначально автор назвал ее «Свободным ящиком» и заявил, что она была «сконструирована для пересылки невозможных объектов в большом количестве»(рис.9).

Рисунок 9. Невозможные ящики

2.Применение невозможных фигур

Невозможные фигуры находят иногда неожиданное применение. Оскар Рутерсвард рассказывает в книге «Omojliga figurer» об использовании рисунков имп-арта для психотерапии [3]. Он пишет, что картины своими парадоксами вызывают удивление, заостряют внимание и желание расшифровать. Психолог Роджер Шепард использовал идею трезубца для своей картины невозможного слона.

В Швеции их применяют в зубоврачебной практике: рассматривая картины в приемной, пациенты отвлекаются от неприятных мыслей перед кабинетом стоматолога.

За рубежом, на улицах городов, мы можем увидеть архитектурные воплощения невозможных фигур.

В последнее время было создано несколько мини скульптур и объемных моделей невозможных фигур. Им даже поставлен памятник.

Треугольник Пенроуза увековечен в городе Петре в Австралии. Он был установлен в 1999 году и теперь все, проходя мимо, могут увидеть невозможную фигуру (рис. 10).

Рисунок 10. Треугольник Пероуза в Австралии

.Невозможные фигуры в живописи

В живописи существует целое направление, которое называется импоссибилизм («невозможность») – изображение невозможных фигур, парадоксов. Интерес к импоссибилизму разгорелся к 1980 году. Этот термин был введен в обращение Тедди Бруниусом, профессором искусствоведения копенгагенского университета. Термин этот точно определяет то, что входит в это новое понятие: изображение предметов, которые кажутся реальными, но не могут существовать в физической реальности.

Фрактальная геометрия изучает закономерности, проявляемые в структуре природных объектов, процессов и явлений, обладающих явно выраженной фрагментарностью, изломанностью и искривленностью.

Оп-арт (англ. Op-art – сокращенный вариант optical art – оптическое искусство) – художественное течение второй половины 20 века, использующее различные зрительные иллюзии, основанные на особенностях восприятия плоских и пространственных фигур. Самостоятельным направлением в оп-арте является так называемый имп-арт (imp-art), использующее для достижения оптических иллюзий особенности отображения трёхмерных объектов на плоскости.

Наиболее известными представителями оп-арте являются Морис Эшер, венгерский художник Иштван Орос, фламандский художник Жос Де Мей, швейцарский художник Сандро дель Пре. Британский художник Джулиан Бивер – один из самых известных художников этого направления, который изображает свои шедевры не на бумаге, а на улицах города, стенах городских домов, где ими могут любоваться все.

Не редко невозможные фигуры используются для оформления обложек журналов.

Учебник по алгебре для 7 класса (рис.11).

Рисунок 11. Учебник Алгебры

Источник

Невозможная фигура

Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия существования такой фигуры в трёхмерном пространстве.

На самом деле все невозможные фигуры могут существовать в реальном мире. Так, все объекты, нарисованные на бумаге, являются проекциями трёхмерных объектов, следовательно, можно создать такой трёхмерный объект, который при проецировании на плоскость будет выглядеть невозможным. При взгляде на такой объект из определённой точки он также будет выглядеть невозможным, но при обзоре с любой другой точки эффект невозможности будет теряться.

Наиболее известные невозможные фигуры: невозможный треугольник, бесконечная лестница и невозможный трезубец.

«Отцом» невозможных фигур является шведский художник Оскар Реутерсвард, который за годы своего творчества нарисовал тысячи таких фигур. Настоящую известность невозможные фигуры обрели, когда их изобразил на своих литографиях известный голландский художник Мауриц Корнелис Эшер.

Направление в изобразительном искусстве, нацеленное на изображение невозможных фигур, называется имп-арт.

Ссылки

Полезное

Смотреть что такое «Невозможная фигура» в других словарях:

ФИГУРА, НЕВОЗМОЖНАЯ — Любая из класса фигур, в которых отдельные компоненты вызывают противоречивые интерпретации. В примере, приведенном здесь, правая сторона имеет сигналы для оценки объекта как двузубчатого, нолевая – как трехзубчатого. Таким образом, такой предмет … Толковый словарь по психологии

Лестница Пенроуза — (бесконечная лестница, невозможная лестница) это одна из основных невозможных фигур, открытая Оскаро … Википедия

Перспектива — У этого термина существуют и другие значения, см. Перспектива (значения). Пример перспективы в фотографии. «Блошиный рынок в Москве, вид с моста до станции … Википедия

Список парадоксов — … Википедия

Парадоксы — Служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не устанавливается на информационные статьи списки и глоссари … Википедия

Натюрморт и улица — Эшер, Мауриц Корнелис Натюрморт и улица, 1937 англ. Still Life and Street Ксилография. 48,7×49 см «Натюрморт и улица» ксилография нидерландского художника Эшера, впервые напечатанная в марте 1937 года, и хранящаяся в коллекции… … Википедия

Словарь терминов шахматной композиции — # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С Т У Ф Х Ц … Википедия

Анна Каренина — У этого термина существуют и другие значения, см. Анна Каренина (значения). Анна Каренина … Википедия

Джоконда — Леонардо да Винчи Мона Лиза, 1503 1505 Ritratto di Monna Lisa del Giocondo Дерево, масло. 76,8 × 53 см Лувр, Париж «Мона Лиза» (итал … Википедия

Мадонна Лиза — Леонардо да Винчи Мона Лиза, 1503 1505 Ritratto di Monna Lisa del Giocondo Дерево, масло. 76,8 × 53 см Лувр, Париж «Мона Лиза» (итал … Википедия

Источник

Что делает невозможную фигуру невозможной?

Jun 27 · 4 min read

Невозможные фигуры образуются линиями, соединенными между собой самым противоречивым образом, с искажением перспективы. При зрительном восприятии таких изображений возникает эффект оптической иллюзии, запредельной реальности. Предлагаю вашему вниманию небольшую коллекцию из этих причудливых фигур.

Треугольник Пенроуза

Автором треугольника Пенроуза, или невозможного треугольника (трибара Пенроуза), является шведский художник Оскар Реутерсвард. Свое знаменитое изображение, принесшее ему славу “отца невозможных фигур”, он создал в 18 лет совершенно случайно. Это произошло в 1934 году на уроке латыни, на котором гимназист Оскар Реутерсвард занимался разрисовыванием учебника.

Внимание широкой публи к и треугольник Реутерсварда привлек в 1950-х годах, когда психиатр Лайонел Пенроуз и его сын сэр Роджер Пенроуз — впоследствии выдающийся математик, лауреат Нобелевской премии — признали “абсолютную невозможность” этой фигуры. В 1958 году в Британском журнале психологии они опубликовали статью “Невозможные объекты: особый тип визуальной иллюзии”. Кроме того, объекты невозможных геометрических форм были представлены в работах голландского художника-графика М. К. Эшера.

В Викисловаре треугольник Пенроуза определяется как “оптическая иллюзия, возникающая при взгляде на невозможный монолитный объект, состоящий из трех прямолинейных брусков квадратного сечения, которые встречаются попарно под прямым углом в вершинах образуемого ими треугольника”.

Из этого описания следует, что линии невозможной фигуры соединены каким-то неправдоподобным образом. Подобные формы могут существовать только вопреки законам евклидовой геометрии.

При рассмотрении этого рисунка может показаться, что правая сторона треугольника удаляется от вас, в то время как левая приближается. Тем не менее, они соединены одним и тем же прямоугольным бруском и находятся в одной плоскости.

В 1854 году Пенроуз посетил лекцию Эшера и был настолько восхищен его магической геометрией, что начал сам придумывать невообразимые конструкции. Одна из них вдохновила Эшера на создание знаменитой литографии “Водопад”.

В рамках той же концепции была создана еще одна невероятная фигура, известная как Невозможный / Иррациональный куб.

Ребра куба кажутся находящимися одновременно впереди и позади, что невозможно с точки зрения геометрии.

Лестница Пенроуза

Лестница Пенроуза — это каскад ступеней, бесконечно ведущих вверх или вниз. Первое впечатление от конструкции приводит в замешательство, в голове возникает вопрос: “Как такое может быть?”. Но стоит вам изменить угол зрения и внимательнее присмотреться к фигуре, как иллюзия исчезает.

Упомянутая выше статья Пенроуза также содержала описание созданной им невозможной лестницы. По словам ученого, эта структура “воспринимается как лестничный пролет, но связи между ее частями таковы, что картина в целом выглядит противоречиво”.

Два года спустя, в 1960 году, в литографии “Восхождение и нисхождение” Эшер запечатлел собственный образ невозможной лестницы. Произошло это под влиянием статьи Пенроуза, в которой тот признавался, что на создание невозможной лестницы его мотивировало творчество Эшера. Получив от Пенроуза копию этой публикации, художник, в свою очередь, выразил ему свое почтение:

“Несколько месяцев назад один мой друг прислал мне фотокопию вашей статьи… Ваши фигуры 3 и 4, “непрерывный лестничный пролет”, поразили меня своей новизной и настолько впечатлили, что в конце концов вдохновили на создание новой картины, которую я хотел бы послать вам в знак моего уважения”.

Примечательно, что изображение невозможной лестницы впервые было создано Оскаром Реутерсвардом в 1937 году, однако ни Пенроуз, ни Эшер ничего не знали об этом

Лестница Пенроуза — это абсолютно невозможная конструкция: визуально поднимаясь или спускаясь по ней, вы останетесь на том же уровне, в каком бы направлении ни двигались — по часовой стрелке (вниз) или против (вверх).

Идея бесконечной лестницы Пенроуза была использована в научно-фантастическом триллере “Начало” (2010) режиссера Кристофера Нолана. Никуда не приводящий лестничный пролет появляется и в боевике “Мстители” (1998).

Более того, в апреле 2014 года была выпущена видеоигра Monument Valley (“Долина монументов”). Ее разработчик — Ustwo Games — впечатлил пользователей множеством оптических иллюзий и невозможных фигур.

Невозможные фигуры выявляют бесконечную одержимость своих творцов всем непостижимым. Но не только в этом их притягательная сила. Они словно говорят нам: “Не верь глазам своим”. Вглядываясь в них, мы понимаем, как легко поддаемся иллюзиям восприятия и как сильно оно отличается от впечатлений других людей, наблюдающих то же самое.

Источник

Невозможные фигуры, особенности их восприятия и применение

Дата публикации: 04.02.2017 2017-02-04

Статья просмотрена: 1097 раз

Библиографическое описание:

Щербинина, Е. А. Невозможные фигуры, особенности их восприятия и применение / Е. А. Щербинина, Д. П. Никифорова. — Текст : непосредственный // Молодой ученый. — 2019. — № 9 (247). — С. 75-83. — URL: https://moluch.ru/archive/247/33195/ (дата обращения: 13.12.2021).

В нынешнее время довольно часто встречаются фотографии, эпизоды из кинематографа, здания, изображения, при виде которых можно воскликнуть «Такого не может быть!». Это и рисунки с искаженной перспективой, и невозможные в нашем трехмерном мире объекты, и немыслимые сочетания вполне реальных предметов. Появившись в начале XI века, такие «странные» рисунки и фотографии сегодня стали целым направлением искусства и архитектуры. Так же школьном курсе изучаются выпуклые и невыпуклые многогранники. В кабинете математики есть невыпуклый многогранник, который называется Флексор Штеффена, данный многогранник создан руками ученика, окончившего нашу школу, и поэтому, увидев данный многогранник, я поставила себе цель, а существуют ли еще многогранники и другие невозможные фигуры, которые можно создать своими руками. [1]

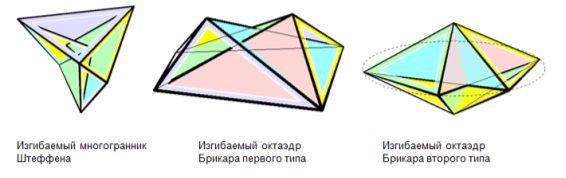
Многогранник (многогранная поверхность) называется изгибаемым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело), а деформация осуществляется только за счёт непрерывного изменения двугранных углов. Такая деформация называется непрерывным изгибанием многогранника [2]. (приложение 1)

До сих пор не существует чёткого определения невозможных фигур. [3].

Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры.

Невозможные фигуры — это геометрически противоречивые изображения объектов, не существующих в реальном трёхмерном пространстве. Невозможность возникает из противоречия между подсознательно воспринимаемой геометрией изображённого пространства и формально-математической геометрией. [2] Невозможные фигуры представлены на Рисунке 1

Рис. 1. Изгибаемые многогранники

Невозможные фигуры были известны ещё в Средневековье, но систематическое их изучение началось лишь в середине XX века. Создателями невозможных фигур называют Оскара Реутерсварда и Роджера Пенроуза [2].

При проецировании трехмерной фигуры на плоскость некоторые линии могут становиться невидимыми, перекрывать друг друга. В качестве примера можно взять знаменитый треугольник Пенроуза, Таблица 1

Создание треугольник Пенроуза

Примечание:

Результат

Предположим, что треугольник Пенроуза можно создать из обычных трёх брусков бумаги

В ходе эксперимента было получено 3 одинаковых бруска из обычной бумаги А4. В ходе склеивания модели, бумага потерпело искажение, тем самым произошло нарушение граней.

Вывод: Невозможно создать треугольник Пенроуза из обычных равных брусков

Но! Треугольник Пенроуза можно создать, если учесть особенность построения фигуры, и согласно определению, линии, невидимые глазу можно исказить. При таком условии, треугольник Пенроуза можно сделать в объёме

Многие люди думают, что невозможные фигуры действительно невозможны, и их нельзя увидеть в реальном мире. На самом деле их можно увидеть в реальности. Надо помнить, что любой рисунок на листе бумаги — это проекция трехмерной фигуры. Следовательно, любая фигура, нарисованная на листе бумаги должна существовать в трехмерном пространстве [4].

Конечно, ни одну из невозможных фигур нельзя создать, действуя прямолинейно. Но можно взять три различных бруска и составить треугольник, представленный на Рисунке 2 [4].

Рис. 2. Треугольник Пенроуза

В зеркале мы видим реальную фигуру. Получается, что приведенная фигура выглядит невозможным треугольником только с единственной точки зрения. Это касается всех невозможных фигур [4].

Области применения невозможных фигур разнообразно. В современном мире они окружают нас практически повсюду. Применение невозможных фигур представлены в Таблице 2.

Области применения невозможных фигур

Область применения

Изображение

В Иконописи: Христианство очень редко использовало модели несуществующих фигур, но их изображения часто встречаются на иконах и фресках. Самым известным из них является изображение невозможного треугольника, расположенного на экране перед алтарем. Он находится в церкви Святой Троицы, простроенной бенединскими монахами с 1150 по 1550 годы. На фресках обычно — это невозможная колоннада. В качестве примера можно привести изображение «Мадонна с младенцем» с миниатюры из книги Генриха II.

В искусстве: Широко известны картины с невозможными фигурами художников, работавших, начиная со средних веков до середины прошлого века.

В филателистке. В 1982 году по заказу правительства Швеции Оскаром Реутерсвардом были выполнены марки с изображениями невозможных фигур. Они выпускались ограниченным тиражом, сегодня являются большой редкостью и пользуются большим спросом

Символика. Невозможные фигуры часто можно встретить в качестве изображений на часах, кружках, футболках.

В архитектуре. Вкачестве примера невозможных фигур в архитектуре можно привести Кубические дома. Они были построены в 1984 году в Роттердаме (Нидерланды) архитектором Пиетом Бломом. Дома развернуты на угол в 45 градусов и расположены по шестиугольной сетке. Конструкция состоит из 32 кубов. Каждый кубический дом состоит из четырех этажей. Крыши домов, окрашенные в белый и серый. Этот комплекс зданий обладает одним интересным свойством. С высоты птичьего полета здания образуют конструкцию, выглядящую как невозможная фигура.

Кубические дома

В кинематографе. Невозможные фигуры приобретают всё большую популярность. Во многом, с моей точки зрения, это заслуга М. К. Эшера. Его работа «Относительность» послужила основой для очень многих сюжетов. Самым, пожалуй, известным является мультсериал «Симпсоны». В эпизоде» Treehouse of Horror VIII» Лиза Симпсон находит невозможный объект, выставленный на продажу, который является ничем иным как невозможным трезубцем.

Аватар

Для полного анализа невозможных фигур было проведено ряд исследований.

Опыт 1. Создание невозможной фигуры по фотографии, найденной в интернете [5]. Эксперимент представлен в Таблице 3.

Создание невозможной фигуры из карандашей. Опыт 1

Примечание

Изображение

Данную картинку можно найти на просторах интернета. Карандаши, равного размера сплетены в единую конструкцию.

Взяв за основу 4 деревянных палочки, одинакового размера, было создано сплетение их по образцу. При сближении к центру, в результате одна палочка была переломлена. На фотографии представлено максимально возможное сближение палочек в данной конструкции

Опыт 2. Создание знаменитой невозможной фигуры — ленты Мёбиуса. Эксперимент представлен в Таблице 4.

Создание невозможной фигуры «Лента Мёбиуса». Опыт 2

Примечание

Изображение

Лента Мёбиуса — самая знаменитая невозможная фигура. Суть этой фигуры, что она в пол оборота завернута. Её невозможно выпрямить и вывернуть.

Создание данной невозможной фигуры — возможно. Сделать её может каждый, и при этом не зная её названия, многие уже воспроизводили её. Лента может быть из любого материала, который можно с одной стороны на один раз свернуть.

Опыт 3. Изучив материал по данной теме [6], был составлен чертёж невозможной фигуры. Эксперимент представлен в Таблице 5.

Создание невозможной фигуры «Лента Мёбиуса». Опыт 3

Примечание

Изображение

Чертёж невозможной фигуры, с расчетом размеров и количества элементов для создания модели из плотной бумаги формата А4.

То что мы видим на картинке скрывает многое с обратной стороны. Искажения, тени, постановка объектов — всё это влияет на построение 3D фигуры. Но невозможные фигуры — возможно создать, нужно только время и терпение. Одна из важных частей невозможных фигур — это иллюзии.

Был проведен опрос среди выпускников школы. В ходе исследования приняло участие 86 человек.

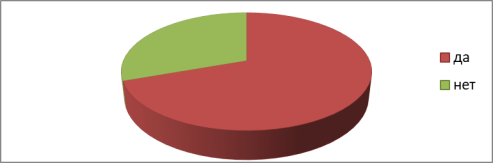
Вопрос 1. Вы что-нибудь знаете о невозможных фигурах? Результаты опроса представлены на Рисунке 3.

Многие выпускники знают о том, что такое невозможная фигура. Кто-то знает определения, а кто-то виды и применение этих фигур. Так что ученики школы имеют представление о этих фигурах.

Рис. 3. Вы что-нибудь знаете о невозможных фигурах?

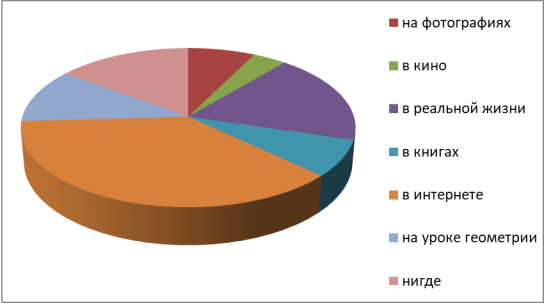
Вопрос 2. Где Вы встречались с невозможными фигурами? Результаты опроса представлены на Рисунке 4.

По результатам анкетирования видно, что иллюзии и невозможные фигуры в основном встречаются в интернете. Именно там многие из выпускников с ними впервые и познакомились. Так же и в реальной жизни наблюдательные подростки замечают невозможные фигуры

Рис. 4. Где Вы встречались с невозможными фигурами?

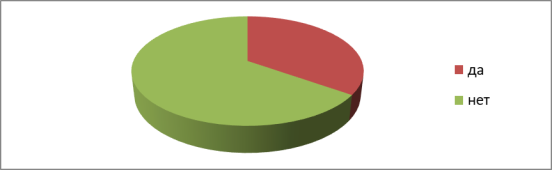
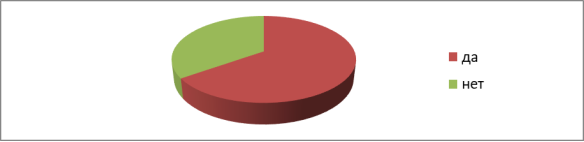
Вопрос 3. Пытались ли вы создать невозможную фигуру? Результаты опроса представлены на Рисунке 5.

40 % выпускников не только увлечены и знают о существовании невозможных фигур, так же они пытались сотворить некоторые из них своими руками. Это свидетельствует о том, что данная тема распространена и увлекает своей «невозможностью» людей, которые хотят проверить самим возможно ли создать фигуры или нет.

Рис. 5. Пытались ли вы создать невозможную фигуру?

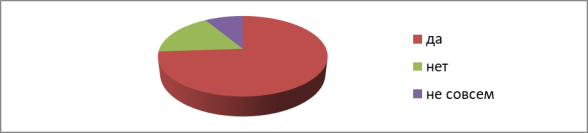
Вопрос 4. Интересно ли вам рассматривать невозможные фигуры и иллюзии? Результаты опроса представлены на Рисунке 6.

75 % выпускников рассматривают невозможные фигуры и ими увлечены. Это показывает то, что данные фигуры очень редко обходят и взгляд к ним приковывается, что подтверждает еще раз Вопрос 3

Рис. 6. Интересно ли вам рассматривать невозможные фигуры и иллюзии?

Вопрос 5. Смотрите ли вы фильмы 3D, в которых существует мир иллюзий? Результаты опроса представлены на Рисунке 7.

Во время исследования, опрошенные задавали вопросы, что имеется в виду по «иллюзиями» в 3D фильмах. Многие и не знали, что подвергаются иллюзиям, точнее не знали, что 3D эффект и называется иллюзией.

Рис. 7. Смотрите ли вы фильмы 3D, в которых существует мир иллюзий?

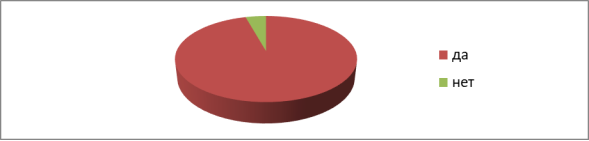
Вопрос 6. Считаете ли вы, что невозможные фигуры — это неотъемлемая часть современного архитектора? Результаты опроса представлены на Рисунке 8.

Практически все опрошенные считают, что невозможные фигуры являются неотъемлемой частью архитектора, — это подчёркивает то, что данная тема актуальна в наше время.

Рис. 8. Считаете ли вы, что невозможные фигуры — это неотъемлемая часть современного архитектора?

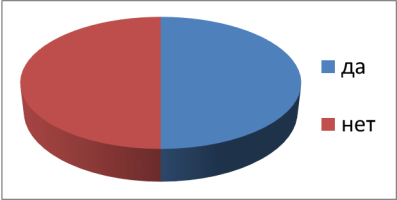
Вопрос 7. Возможно ли создать данную фигуру? Результаты опроса представлены в Таблице 6

Ответы разделились поровну. 50 % считает, что данная невозможная фигура — невозможна. Из этого следует, что они не знают о невидимых линиях, и искажениях.

Возможно ли создать данную фигуру?

Представленное изображение невозможной фигуры

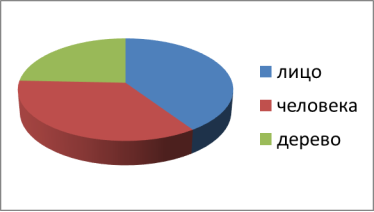
Вопрос 8. Что вы видите на фотографии? Результаты опроса представлены в Таблице 7

Данное изображение показывалось ровно 7 секунд. Видения различались. Это доказывает то, что каждый человек по-своему смотрит на иллюзии. Но треть увидела два элемента на рисунке, а половина из этих увидели все три элемента сразу.

Что вы видите на фотографии?

В результате проведенного опроса можно сделать вывод насколько восприятие человека разница. В данном опросе не учитывалась половая принадлежность. Опрошенные многие не только знают о невозможных фигурах, но и сталкивались с ними, и многим данная область вызывает интерес. Восприятие зависит от многих факторов, которые в работе не были учтены: свет, возраст, время, предпочтения опрошенных, а также внимания.

Эта тема актуальна в настоящее время. Изучение невозможных фигур имеет довольно важное значение не только с точки зрения геометрии, но и с точки зрения искусства. Они широко используются в современной рекламе, промышленной графике, плакате, оформительском искусстве и логотипах различных фирм.

Невозможные фигуры, пожалуй, самые завораживающие из всех существующих оптических иллюзий.

2. Сайт «Невозможный мир» http://im-possible.info/russian/articles/

Похожие статьи

Развитие творческого мышления учащихся при изучении понятий.

При этом составляется таблица, включающая столбцы с названиями тела, количество вершин, количество граней, количество ребер, сумма

При изучени многогранников большую пользу приносит классификация многогранников. При этом многогранник определяется как часть.

Похожие статьи

Развитие творческого мышления учащихся при изучении понятий.

При этом составляется таблица, включающая столбцы с названиями тела, количество вершин, количество граней, количество ребер, сумма

При изучени многогранников большую пользу приносит классификация многогранников. При этом многогранник определяется как часть.

Источник