Что называют неправильной дробью
Дроби
Что такое дробь
Дроби нужны для обозначения нецелых количеств. Они образуются как результат деления натуральных чисел, когда делимое не кратно делителю.
Дробная черта равносильна знаку деления. То есть \(4:6=\frac46\) (четыре шестых), \(7:2=\frac72\) (семь вторых). Числитель дроби играет роль делимого, а знаменатель — делителя.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Знаменатель дроби не может быть нулем.
Основные свойства дробей
Несократимой называют дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме 1 (-1).
Существует два вида дробей: правильные и неправильные.
Неправильные дроби всегда больше правильных: \(\frac <39>
Правильные дроби
Правильная дробь — это обыкновенная дробь, числитель которой меньше знаменателя.
Правильная дробь называется так, поскольку выражает «правильную» часть единицы, то есть часть, которая меньше целого: \( \frac25
Таким образом, отличить правильную дробь от неправильной можно при сравнении дробей с единицей. Это различие не влияет на арифметические действия, но важно при сравнении дробей.
Смешанные дроби
Неправильные дроби не принято оставлять в результате вычислений. Лучше преобразовывать их в смешанные числа. Любую неправильную дробь можно представить в виде смешанного числа.
Смешанное число — это число, содержащее целую и дробную часть.
Для составления смешанной дроби необходимо:
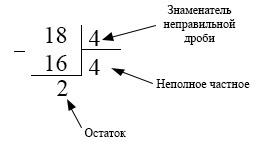
Записать неправильную дробь \(\frac<18>4\) в виде смешанной.
Тогда искомая смешанная дробь \(\frac<18>4=4\frac24.\) Эту дробь можно сократить, поделив числитель и знаменатель дробной части на общий делитель 2:
Смешанное число можно записать в виде неправильной дроби. Для этого необходимо целую часть умножить на знаменатель дробной части. К полученному числу нужно прибавить числитель дробной части. Эту сумму записать в числитель, а знаменатель дробной части оставить без изменений.
Смешанное число \(6\frac25\) записать в виде неправильной дроби.
Как перевести правильную дробь в неправильную
Перевести правильную дробь в неправильную или наоборот невозможно. Это разные категории чисел.
Любое натуральное число можно представить в виде неправильной дроби: \(2=\frac21.\)
Дробь с числителем p и знаменателем 1 — это другая форма записи натурального числа p. Это правило можно представить в виде формулы: \(p=\frac p1.\)
Действия с дробями, как решать примеры
Приведение к общему знаменателю
Чтобы решать большинство примеров с дробями, необходимо приводить их к общему знаменателю. Чтобы привести дроби \(\frac ab\) и \(\frac cd\) к общему знаменателю, необходимо:
Сравнение
Чтобы сравнить обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители. Дробь с большим числителем больше.
\(\frac34>\frac13,\) поскольку \(\frac9<12>>\frac4<12>.\)
Если сравниваются смешанные числа, в первую очередь необходимо смотреть на целую часть. Больше то число, целая часть которого больше.
К примеру, \(8\frac16>5\frac23.\)
Если целые части смешанных чисел равны, то сравнивают дробные части по правилу сравнения обыкновенных дробей. Число с наибольшей дробной частью будет больше: \(5\frac23>5\frac13.\)
Сложение и вычитание
Чтобы сложить обыкновенные дроби, необходимо привести их к общему знаменателю, сложить числители, а знаменатели оставить без изменений. При необходимости привести дробь в вид смешанного числа.
При сложении смешанных чисел целые и дробные части складываются отдельно.
Чтобы вычесть одну дробь из другой, также необходимо привести их к общему знаменателю, после чего вычесть числители, а знаменатели оставить без изменений.
Умножение и деление
Чтобы умножить обыкновенные дроби, необходимо перемножить их числители и знаменатели.
\(\frac ab\cdot\frac cd=\frac
Умножить дробь \(\frac35\) на \(\frac23.\)
При умножении дроби на натуральное число, нужно умножить числитель на это число, а знаменатель оставить тем же. Так происходит, поскольку любое натуральное число можно представить в виде \(p=\frac p1.\)
\(\frac ab\cdot p=\frac ab\cdot\frac p1=\frac
Чтобы умножить смешанные числа, необходимо сперва представить их в виде обыкновенных дробей и лишь затем совершать действие.
Чтобы поделить одну дробь на другую, нужно умножить первую дробь на дробь, обратную второй. При этом оба знаменателя и числитель второй дроби не должны быть равны нулю.
\(\frac ab:\frac cd=\frac ab\cdot\frac dc=\frac
Поделить дробь \(\frac34\) на \(\frac23.\)
При делении смешанных чисел, как и при умножении, их необходимо сперва привести к виду обыкновенной дроби.
Правильные и неправильные дроби.
Виды дробей.
Как вы уже заметили дроби бывают разные. Например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, \frac<7><7>, \frac<13><5>, …\)
Делятся дроби на два вида правильные дроби и неправильные дроби.
В правильной дроби числитель меньше знаменателя, например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, …\)
В неправильной дроби числитель больше или равен знаменателю, например, \(\frac<7><7>, \frac<9><4>, \frac<13><5>, …\)
Правильная дробь всегда меньше единицы. Рассмотрим пример:
Единицу мы можем представить как дробь \(1 = \frac<3><3>\)
Знаменатели одинаковые равны числу 3, далее сравниваем числители.
Вопросы по теме “Правильные или неправильные дроби”:
Может ли правильная дробь быть больше 1?
Ответ: нет.
Может ли правильная дробь равна 1?
Ответ: нет.
Может ли неправильная дробь меньше 1?
Ответ: нет.
Пример №1:
Напишите:
а) все правильные дроби со знаменателем 8;
б) все неправильные дроби с числителем 4.
Решение:
а) У правильных дробей знаменатель больше числителя. Нам нужно в числитель поставить числа меньшие 8.
\(\frac<1><8>, \frac<2><8>, \frac<3><8>, \frac<4><8>, \frac<5><8>, \frac<6><8>, \frac<7><8>.\)
б) В неправильной дроби числитель больше знаменателя. Нам нужно в знаменатель поставить числа меньшие 4.
\(\frac<4><4>, \frac<4><3>, \frac<4><2>, \frac<4><1>.\)
Пример №2:
При каких значениях b дробь:
а) \(\frac<12>\) будет правильной;
б) \(\frac<9>\) будет не правильной.
Решение:
а) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
б) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9.
Задача №1:
Сколько минут в часе? Какую часть часа составляет 11 мин.?
Ответ: В часе 60 минут. Три минуты составят \(\frac<11><60>\) часа.
Какую дробь называют правильной в математике
Правильная дробь — что это такое в математике
Дробью в математике называют число, в состав которого входит одна либо несколько равных частей (или долей) от единицы.
Виды дробей в зависимости от формы записи:
Здесь число, которое расположено над чертой, является числителем. Под чертой расположен знаменатель. Числитель представляет собой делимое, а знаменатель играет роль делителя.
Правильная дробь — дробь с числителем, модуль которого меньше по сравнению с модулем знаменателя.
Неправильная дробь — дробь с числителем, модуль которого больше, чем модуль знаменателя, либо равен ему.
Любое число, которое является целым и не равно нулю, можно записать, как неправильную обыкновенную дробь. Знаменатель при этом будет равен 1.
Основное свойство дроби можно сформулировать таким образом: когда числитель и знаменатель, которые принадлежат одной дроби, умножают, либо делят на одно и то же число, дробь не поменяется, изменится лишь ее запись. К примеру:
1 5 = 1 × 2 5 × 2 = 2 10
Чем отличается правильная от неправильной и смешанной, как определить
Правильная дробь отличается тем, что имеет числитель, который меньше знаменателя.
В качестве наглядного примера можно записать правильные дроби:
Заметим, что во всех записанных случаях числитель меньше, чем знаменатель.
По сравнению с неправильной дробью правильная дробь всегда меньше 1. Тогда как неправильная дробь больше, либо равна 1.
Сравнение разных типов дробей:
Действия с правильными дробями, как найти
Правильные дроби можно встретить при решении множества задач по математике. Для них предусмотрены все действия, которые выполняют с обыкновенными дробями.
Приведение к общему знаменателю
Перед тем, как сравнить, сложить или вычесть дроби, требуется выполнить их преобразование. В результате арифметических действий дроби должны пробрести одинаковые знаменатели. К примеру, имеется пара дробей:
В результате знаменатели первой и второй дроби становятся одинаковыми и равными M. Допустимо заменить минимальное единое кратное при решении несложных примеров на какое-либо другое общее кратное. К примеру, таким кратным может стать произведение знаменателей.
Сравнение
С целью сравнения пары обыкновенных дробей необходимо выполнить операцию приведения их к единому знаменателю. Далее следует сравнить числители дробей, которые в итоге получились. Если числитель больше, то и дробь считается больше.
Далее необходимо привести дроби к знаменателю, равному 20.
3 4 = 15 20 ; 4 5 = 16 20
Сложение и вычитание
Прибавить одну обыкновенную дробь к другой обыкновенной дроби можно. Но перед этим требуется выполнить приведение этих дробей к единому знаменателю. После такой операции находят сумму числителей, а знаменатели оставляют без изменений.
1 2 + 1 3 = 3 6 + 2 6 = 5 6
НОК знаменателей для 2 и 3 составляет 6. Следует привести дробь 1 2 к знаменателю 6. Чтобы получить такой результат, необходимо выполнить умножение числителя и знаменателя на 3. В результате получим:
Затем требуется привести дробь 1 3 к аналогичному знаменателю. При этом нужно выполнить умножение числителя и знаменателя 2. Получим в итоге:
Похожий алгоритм действий предусмотрен для вычитания дробей. Перед тем, как посчитать их разность, следует привести дроби к общему знаменателю. Далее вычитают числители. Знаменатель при этом не меняется.
1 2 — 1 4 = 2 4 — 1 4 = 1 4
НОК знаменателей 2 и 4 составляет 4. Выполняя приведение дроби 1 2 к знаменателю 4, необходимо найти произведение числителя, знаменателя и числа 2. В результате получим:
Умножение и деление
При умножении двух обыкновенных дробей требуется выполнить умножение их числителей и знаменателей:
Рассмотрим частный случай умножения дроби на натуральное число. Для этого следует найти произведение числителя и данного числа, а знаменатель остается без изменений.
Когда числитель и знаменатель полученной дроби не являются взаимно простыми, необходимо такую дробь сократить:
5 8 · 2 5 = 10 40 = 1 4
В процессе деления одной обыкновенной дроби на другую требуется выполнить умножение первой дроби на дробь, которая является обратной для второй:
Возведение в степень и извлечение корня
Дроби можно возводить в степень. При этом необходимо выполнить арифметическое действие возведения в степень отдельно со знаменателем и числителем этой дроби:
2 3 3 = 2 3 3 3 = 8 27
Из дробей можно извлекать корень. Для того чтобы справиться с подобной задачей, необходимо извлечь заданный корень отдельно из числителя и знаменателя:
Перевод других видов дробей в правильную форму
Для того чтобы перевести неправильную дробь в правильную, либо для выполнения обратного действия, требуется соблюдать определенный порядок. Прямой перевод невозможен. Результатом подобной операции будет являться преобразованная запись, которая содержит в себе целую, а также дробную части. Последовательность действий:
С помощью достаточно простого метода удобно переводить числа из одной формы в какую-либо другую. Данный алгоритм можно записать в виде математического уравнения:
n a ÷ b = ( ( n × b ) + a ) ÷ b
Смешанное отношение представляет собой сумму из целого и части. Для того чтобы понять, как преобразовать дроби, следует выполнить сложение в качестве арифметического действия. В процессе первое слагаемое нужно записать в виде неправильной дроби путем деления целого на 1. Далее целесообразно воспользоваться правилом сложения дробей. Выполняется поиск общего знаменателя, дополнительных множителей, сложение в числителе. Формула имеет такой вид:
n a ÷ b = n ÷ 1 + a ÷ b = ( ( n × b ) + a ) ÷ b
Неправильную дробь превратить в обычную можно с помощью перевода ее в смешанную. В процессе выражение записывают в виде суммы натурального числа и правильной дроби:
Более простой способ преобразования дробей заключается в представлении делимого, как суммы дробей. При этом важно, чтобы при делении одной из них не было остатка:
m ÷ n = ( k + c ) ÷ n = k ÷ n + c ÷ n
Примеры задач с решением
В учебнике 100 листов. Ученик прочел ½ от общего количества страниц. Необходимо определить число листов, которые прочитал ученик.
Ответ: ученик прочитал 50 листов в учебнике.
Имеется емкость из стекла, наполненная водой, весом 550 гр. Половину воды вылили, а масса оставшейся составила 300 гр. Требуется рассчитать начальный вес воды и массу пустой емкости.
Значение массы воды, которую вылили:
250 гр. является половиной от всей воды, тогда вся вода весит:
Ответ: сначала в емкости было 500 гр. воды, массы емкости составляет 50 гр.
В кассе хранится сумма в 450 рублей. Необходимо определить количество денег в кассе после изъятия 1/3 от всей суммы.
Урок 35 Бесплатно Правильные и неправильные дроби
На этом уроке мы вспомним, что такое обыкновенная дробь.
Рассмотрим, какие виды обыкновенных дробей существуют и выясним, какую дробь считают правильной, а какую неправильной и научимся сравнивать их.
Определим месторасположение правильной и не правильной дроби на координатном луче.
Разберем несколько задач на нахождение части целого и целого по его части, в которых часть представлена в виде обыкновенной неправильной дроби.
Правильные дроби
Вам уже известно, что дробь представляет собой часть некоторой величины.
Обыкновенная дробь записывается двумя числами, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).
Число, стоящее над дробной чертой, называют числителем.
Числитель показывает, сколько долей взяли от целого.
Число, стоящее под дробной чертой, называют знаменателем.
Знаменатель показывает, на сколько всего равных долей разделили целое.
Дробь можно получить следующим образом: разделить целое на равные части и взять несколько из этих частей.
В качестве примера рассмотрим такую ситуацию.
Плитку молочного шоколада разделили на 8 равных долек и из них взяли и съели 4.
Восемь долек шоколадки- это одна целая плитка шоколада.
Одна долька этой шоколадки представляет собой 1/8 всей плитки.
Четыре дольки из восьми можно записать дробью, получим дробь 4/8 (четыре восьмых).
Дробь 4/8 указывает на то, что целое разделили на восемь равных частей и из них взяли четыре.
8 (общее количество долей)- знаменатель дроби 4/8.
4 (количество долей, которые взяли)- числитель дроби 4/8.
Обратим внимание на члены этой дроби (числитель и знаменатель).
4 и 8— это два натуральных числа, причем если их сравнить, то мы можем заметить, что число 4 меньше 8, т.е. числитель меньше знаменателя.
Обыкновенная дробь, в которой числитель меньше знаменателя, называется правильной дробью.
Давайте выясним являются ли дроби 5/8, 6/8, 7/8 правильными.
Для данной дроби 5— это числитель, 8— это знаменатель.
Одну и ту же обыкновенную дробь можно представить разными способами.
Разделить целое на четыре части и взять две, будет тоже самое, что разделить это целое на две части и взять одну.
Такой же результат получится, если разделить все тоже целое на шесть равных частей и взять из них три и т.д.
Существует бесконечное множество дробей, равных половине целого.
Так, например, одна вторая получается, и в таких случаях: целое разделить на восемь частей и взять из них четыре (1/2 = 4/8), из десяти частей взять пять (1/2 = 5/10), из пятидесяти частей взять двадцать пять (1/2 = 25/50) и т.д.
Пройти тест и получить оценку можно после входа или регистрации
Неправильные дроби
Выясним, какую дробь называют неправильной на следующем примере:
На праздник купили один большой торт и разрезали его на девять одинаковых частей (9 долей).
Каждый гость съел по кусочку этого торта, в результате торта больше не осталось.
Получается, что гости съели девять кусочков торта из девяти возможных.
В таком случае дробь \(\mathbf<\frac<9><9>>\) будет показывать, что целое (весь торт) разделили на 9 долей и потом все эти 9 частей взяли, т.е. съели весь торт.
В данной дроби 9 (общее количество долей)- знаменатель дроби \(\mathbf<\frac<9><9>>\).
9 (количество долей, которые взяли)- числитель дроби \(\mathbf<\frac<9><9>>\).
Очевидно, что дробь \(\mathbf<\frac<9><9>>\) будет равна единице.
Любая дробь, в которой числитель равен знаменателю, равна единице.
Дробь \(\mathbf<\frac
Давайте выясним может ли обыкновенная дробь больше единицы.
Рассмотрим еще одну ситуацию.
Допустим, на праздник купили два одинаковых торта.
Каждый торт разрезали на девять равных частей.
За все время праздника гости съели 13 кусочков торта.
От второго торта осталось 5 несъеденных куска.
Когда разделили оба торта на 9 равных частей, в итоге получили 18 одинаковых кусочков (равных долей), они составляют два целых торта.
\(\mathbf<\frac<9><9>>\)— первый торт.
\(\mathbf<\frac<9><9>>\)— второй торт.
Получается из этих 18 кусочков съели 13, т.е. 1 целый торт и еще 4 кусочка.
Четыре кусочка от второго торта будут выражаться дробью \(\mathbf<\frac<4><9>>\).
В таком случае получаем \(\mathbf<\frac<9><9>>\) (один целый торт), да еще \(\mathbf<\frac<4><9>>\) второго торта- это часть кусочков торта, которые съели.
9 долей первого торта + 4 доли второго торта = \(\mathbf<\frac<13><9>>\) торта съели на празднике.
Так как каждый торт был разрезан на 9 частей, то в знаменателе дроби \(\mathbf<\frac<13><9>>\) стоит цифра 9.
Осталось пять частей торта, т.е. \(\mathbf<\frac<5><9>>\) торта- часть второго торта.
Обратите внимание на дроби \(\mathbf<\frac<9><9>>\) и \(\mathbf<\frac<13><9>>\).
В дроби \(\mathbf<\frac<9><9>>\) знаменатель равен 9 (общее количество долей), числитель равен 9 (количество долей, которые взяли).
9 = 9- числитель равен знаменателю.
В дроби \(\mathbf<\frac<13><9>>\) знаменатель равен 13 (общее количество долей), числитель равен 9 (количество долей, которые взяли).
13 > 9— числитель больше знаменателя.
Обыкновенную дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.
Правило: Любая неправильная дробь больше единицы или равна ей.
У меня есть дополнительная информация к этой части урока!
Необходимо понимать, что термин «неправильная» не говорит о том, что дробь неверная и с ней невозможно производить различные математические операции.
Дробь называют неправильной, так как она отличается от стандартного понимания дроби.
Неправильная дробь всегда содержит некоторую целую часть и дробную.
На следующих занятиях мы научимся выделять целую и дробную часть и производить с такими числами различные арифметические операции
Любое натуральное число можно представить в виде неправильной дроби, данная запись будет выглядеть так:
Дробь с числителем а, где а— любое натуральное число, и знаменателем, равным единице- это еще одна верная форма записи натурального числа а.
Натуральное число 3 = \(\mathbf<\frac<3><1>>\)
\(\mathbf<\frac<3><1>>\)- неправильная дробь, так как числитель (3) больше знаменателя (1).
\(\mathbf<\frac<24><1>>\)- неправильная дробь, так как числитель (24) больше знаменателя (1).
\(\mathbf<\frac<1245><1>>\)- неправильная дробь, так как числитель (1245) больше знаменателя (1).
Сравнивая правильную и неправильную дробь, можно однозначно сказать, что любая неправильная дробь больше правильной.
Определите какая из дробей \(\mathbf<\frac<7><8>>\) и \(\mathbf<\frac<8><7>>\) больше, какая меньше.
\(\mathbf<\frac<7><8>>\)— правильная дробь (числитель меньше знаменателя), а \(\mathbf<\frac<8><7>>\)— неправильная дробь (числитель больше знаменателя), следовательно \(\mathbf
В математике различают два вида обыкновенных дробей:
1. Правильная (числитель меньше знаменателя).
2. Неправильная дробь (числитель больше знаменателя или равен ему).
Выясним, где на координатном луче изображают правильные и неправильные дроби.
Любому дробному числу соответствует конкретное место на координатном луче.
Чтобы обозначить на координатном луче точку с координатой \(\mathbf<\frac
Чтобы найти число \(\mathbf<\frac<1>
Рассмотрим поясняющий пример.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Определим расположение точек A(\(\mathbf<\frac<2><6>>\)), B(\(\mathbf<\frac<11><6>>\)), D(\(\mathbf<\frac<6><6>>\)) на координатном луче.
Так как знаменатель каждой данной дроби равен шести, то разобьем единичный отрезок ОЕ на шесть равных частей-отрезков, каждая часть будет равна \(\mathbf<\frac<1><6>>\) ОЕ.
Правильная дробь \(\mathbf<\frac<2><6>>\) представляет собой две части (доли) из шести.
Следовательно, точка А(\(\mathbf<\frac<2><6>>\)) удалена от начала координат на расстояние двух отрезков, равных одной доле единичного отрезка- \(\mathbf<\frac<1><6>>\) ОЕ.
Отметим тот факт, что \(\mathbf<\frac<2><6>>\) правильная дробь, а это значит она меньше единицы.
На координатном луче данная точка располагается между числами 0 и 1, т.е. левее точки E(1).
Выясним, где на координатном луче будет располагаться точка D (\(\mathbf<\frac<6><6>>\)).
Известно, что дробь, у которой числитель равен знаменателю, представляет собой неправильную дробь, равную единице.
Дробь \(\mathbf<\frac<6><6>>\) означает шесть частей из шести- это единица.
Отметим точку D (\(\mathbf<\frac<6><6>>\)) на координатном луче, для этого отсчитаем 6 отрезков от начала координат, в результате попадаем в точку Е(1).
Точка с координатой \(\mathbf<\frac<6><6>>\) совпадает с точкой Е(1), в результате получаем сам единичный отрезок ОЕ.
Обозначим на координатном луче точку В с координатой \(\mathbf<\frac<11><6>>\).
Дробь \(\mathbf<\frac<11><6>>\) означает шесть частей (т.е. один единичный отрезок ОЕ) и еще пять таких частей.
Отложим от начала координат один единичный отрезок и от него отсчитаем еще пять делений, каждый из которых равен \(\mathbf<\frac<1><6>>\) единичного отрезка (в общем говоря, нам необходимо отсчитать от начала координат 11 делений, равных \(\mathbf<\frac<1><6>>\) ОЕ).
Нам несложно заметить, что неправильная дробь, у которого числитель больше знаменателя, лежит на координатном луче правее единицы.
На самом деле, такая неправильная дробь выражает некоторую целую часть, да еще часть целого.
Пройти тест и получить оценку можно после входа или регистрации