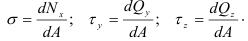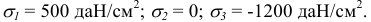Что называют напряжением в данной точке сечения

изучаем сопротивление материалов

Напряжения

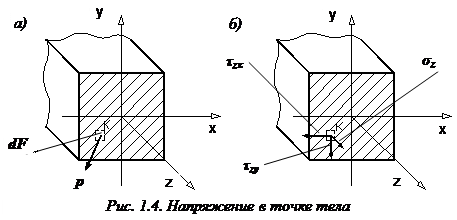
Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_, \tau_[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.

Тензор напряжений

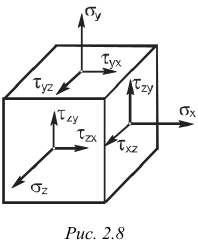
Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений

$$ T _\sigma = \left[\matrix <
\sigma _x & \tau _ & \tau _ \\
\tau _ & \sigma _y & \tau _ \\ \tau _ & \tau _ & \sigma _z
>\right]$$

Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.

При повороте осей координат, совпадающих с нормалями к граням выделенного
элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.

В каждой точке можно провести три взаимно-перпендикулярных главных площадки.

При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).

Связь внутренних усилий и напряжений

Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.

Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:

Выполнив интегрирование по площади поперечного сечения получим:

То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.

1 Проекция вектора полного напряжения на нормаль к данной площадке называется нормальным напряжением и обознача­ется через σ_n.

Источник

Понятие о напряжениях

Понятие о напряжениях

Напряженное состояние в точке

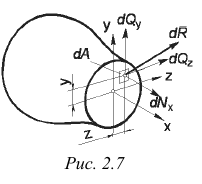
Внутренние усилия, которые были найдены выше из уравнений статики, не являются реальными, а представляют собой лишь статический эквивалент этих усилий, распределенных по всей площади рассматриваемого сечения. Иначе говоря, найденные усилия являются равнодействующими действительных внутренних сил, возникающих в каждой точке сечения. В сечении части А (рис. 2.6, б) выделим элементарную площадку 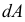(рис. 2.7).

В силу малости элемента можно считать, что внутренние усилия, приложенные к его различным точкам, одинаковы по величине и направлению. Тогда равнодействующая их будет проходить через центр тяжести площади элемента , координаты которого равны и .

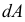
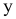
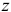
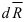
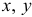
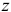
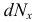
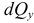
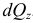
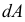
Проектируя вектор на оси и , получим элементарную продольную силу и элементарные поперечные силы и . Разделив эти усилия на площадь , получим величины внутренних сил, приходящихся на единицу площади, рис. 2.7:

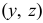
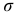
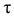
Эти величины называют напряжениями в точке поперечного сечения тела, причем — нормальное напряжение; — касательное напряжение.

Нормальные и касательные напряжения

Нормальные и касательные напряжения представляют собой интенсивность распределения соответственно нормальных и поперечных сил, действующих по элементарной площадке в рассматриваемой точке.

Через любую точку упругого тела, подверженного действию внешней нагрузки, можно провести бесчисленное множество сечений (площадок), по которым в общем случае будут действовать как нормальные, так и касательные напряжения. При этом величина и направление указанных напряжений в каждом конкретном случае будут зависеть от ориентации площадки.

Деформация нагруженного тела сопровождается изменением расстояний между его частицами. Внутренние силы, возникающие между частицами, изменяются под действием внешней нагрузки до тех пор, пока не установится равновесие между внешней нагрузкой и внутренними силами сопротивления. Полученное состояние тела называют напряженным состоянием. Оно характеризуется совокупностью нормальных и касательных напряжений, действующих по всем площадкам, которые можно провести через рассматриваемую точку. Исследовать напряженное состояние в точке тела — значит получить зависимости, позволяющие определить напряжения по любой площадке, проходящей через указанную точку.

Для исследования напряженного состояния в окрестности исследуемой точки тела обычно выделяют элемент в виде бесконечно малого параллелепипеда (рис. 2.8). На его гранях действуют внутренние силы, заменяющие воздействие удаленной части тела и вызывающие появление напряжений. Полные напряжения на гранях можно разложить на нормальные и касательные составляющие. Если ориентацию выделенного элемента изменить, то действующие на его гранях напряжения будут также изменяться. При этом можно найти такое положение элемента, при котором на его гранях касательные напряжения равны нулю.

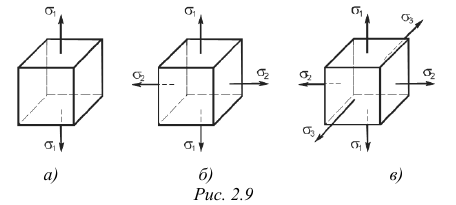
Грани элемента, по которым касательные напряжения не действуют, называют главными площадками, а нормальные напряжения на них — главными напряжениями.

Доказано, что в каждой точке тела имеются по крайней мере три главные площадки, причем они всегда взаимно перпендикулярны.

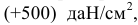
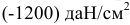
Следовательно, в каждой точке будут также три главных напряжения, линии действия которых определяют три главных направления напряженного состояния в данной точке. Главные напряжения принято обозначать так, чтобы наибольшее из них (в алгебраическом смысле) имело индекс 1, а наименьшее — индекс 3. Например, если одно из главных напряжений равно нулю, другое , а третье — , то

В зависимости от величины главных напряжений различают следующие виды напряженного состояния в точке: линейное, или одноосное — только одно главное напряжение (любое из трех) отлично от нуля, а два других равны нулю (рис. 2.9, а); плоское, или двухосное — два главных напряжения отличны от нуля (рис. 2.9, б); объемное, или трехосное — все главные напряжения отличны от нуля (рис. 2.9, в).

На практике чаще всего имеют место два первых вида напряженного состояния.

Эта теория взята со страницы лекций по предмету «прикладная механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Напряжение в точке тела

Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения.

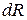
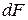
Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы , возникающей на бесконечно малой площадке в окрестности данной точки (рис. 1.4, а).

В количественном выражении .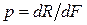

Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, действующем, например, внутри жидкости. Однако давление в точке жидкости одинаково во всех направлениях. Если проведем через точку K тела другое сечение, иной будет внутренняя сила. Следовательно, иным будет и напряжение, хотя оно возникает в той же самой точке K.

Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).

Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.

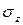
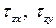
Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение ( – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения ( – тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.

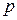
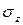
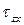
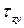
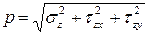
Между полным (), нормальным () и касательными напряжениями ( и ) существует зависимость:

.

Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части.

Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы:

1 МПа = 106 Па; 1 кН/см2 = 107 Па.

Источник

iSopromat.ru

Напряжение в механике — это мера интенсивности распределения внутренних сил R в окрестности точки в пределах данного сечения площадью A.

Таким образом, напряжения p измеряются в единицах силы, отнесенной к единице площади dA
Полные напряжения в точке
Единица измерения напряжений — Паскаль (Н/м 2 =Па).
Рассмотрим подробнее:

Система приложенных к телу внешних нагрузок, приводит к возникновению в его сечениях внутренней силы R и момента M

Внутренние сила и момент в сечении бруса

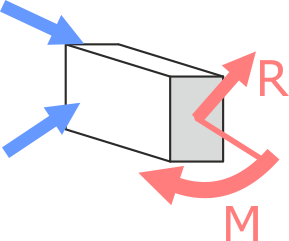
При этом надо понимать что внутренняя сила и внутренний момент воздействуют на всё сечение бруса в целом.

Выделим в рассматриваемом сечении элементарную площадку dA бесконечно малой площади.

Элементарная площадка в сечении бруса

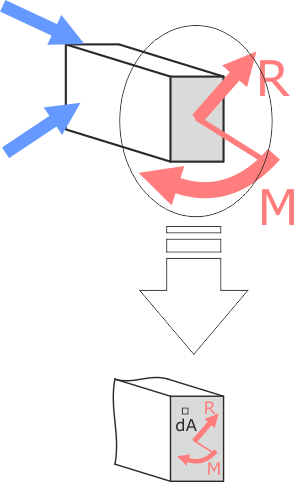
Полное напряжение – часть внутренних усилий, приходящаяся на конкретную точку сечения.

Вектор полного напряжения в точке

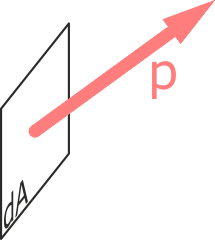
Обозначение полного напряжения в точке – p.
Единица измерения – Паскаль [Па] (Н/м 2 ).

Ввиду того, что большинство конструкционных материалов обладает высокой прочностью часто напряжения, возникающие в них, измеряются в кратных величинах, например мегапаскаль [МПа].

В общем случае вектор полного напряжения в точке может располагаться под любым углом к сечению. В таких случаях для существенного упрощения расчетов его удобно раскладывать на составляющие (проекции):

Нормальное и касательное напряжения

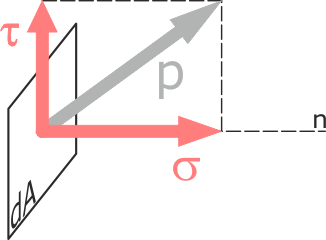
Проекция вектора полного напряжения p на нормаль к сечению называется нормальным напряжением и обозначается через σ, а проекция вектора полного напряжения на плоскость сечения называется касательным напряжением и обозначается через τ.

Разложение вектора полного напряжения на две указанные составляющие имеет конкретный физический смысл – с нормальным напряжением связано разрушение путем отрыва, а с касательным – разрушение путем сдвига или среза.

В частных случаях (например при растяжении-сжатии и кручении) в поперечных сечениях бруса имеют место только нормальные и только касательные напряжения соответственно.

При решении таких задач, величина нормальных и касательных напряжений сравнивается с соответствующими допустимыми значениями напряжений.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Понятие о напряжениях. Нормальные и касательные напряжения.

Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции.

Выделим на плоскости сечения площадку DA; по этой площадке будет действовать внутренняя сила DR. Величина отношения DR/DA=p_ср называется средним напряжением на площадке DA. Истинное напряжение в точке А получим устремив DA к нулю

Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения.

Очевидно, что . Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τ_zх, τ_zу). Размерность напряжений – Н/м 2 (Па).

17. Понятие о напряжениях. Нормальные и касательные напряжения.

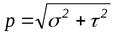
Внутренние силовые факторы. Метод сечений. Эпюры. Выражение внутренних силовых факторов через нормальные и касательные напряжения.

Внутренние силовые факторы

В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы.

По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций.

Чтобы численно установить величину внутренних сил пользуются методом сечений.

Метод сеченийсводится к четырем действиям:

1. Разрезают (мысленно) тело плоскостью в том месте, где нужно определить внутренние силы (рис. 7);

Рис. 7

2. Отбрасывают любую отрезанную часть тела (желательно наиболее сложную), а ее действие на оставшуюся часть заменяют внутренними силами, чтобы оставшаяся исследуемая часть находилась в равновесии (рис.8);

Рис. 8

3. Приводят систему сил к одной точке (как правило, к центру тяжести сечения) и проецируют главный вектор и главный момент системы внутренних сил на нормаль к плоскости (ось ) и главные центральные оси сечения ( и ).

Полученные силы (N, Qy, Qz) (рис. 9) и моменты (Мк, Мy, Mz) называют внутренними силовыми факторами в сечении

Рис. 9

Для внутренних силовых факторов приняты следующие названия:

—продольная или осевая сила;

и —поперечные силы;

—крутящий момент;

и —изгибающие моменты.

4. Находят внутренние силовые факторы, составляя шесть уравнений равновесия статики для рассматриваемой части рассеченного тела.

Эпю́ра (фр. epure — чертёж) — особый вид графика, показывающий распределение величины нагрузки на объект. Например, для стержня продольная ось симметрии берётся за область определения и составляются эпюры для сил, напряжений и разных деформаций в зависимости от абсциссы.

Расчёт эпюр напряжения является базовой задачей такой дисциплины, как сопротивление материалов. В частности, только при помощи эпюры возможно определить максимально допустимую нагрузку на материал.

Для построения ординаты эпюры M в каком либо сечении стержня

необходимо выполнить следующие две операции.

1. С помощью уравнения равновесия ∑M(слева)= 0 для левой отсеченной

части стержневой системы (или ∑M(справа) = 0 для правой части) подсчитать

численное значение изгибающего момента в сечении.

2. Отложить найденное численное значение в виде ординаты перпендикулярно оси стержня со стороны растянутого волокна стержня.

Численное значение изгибающего момента в сечении равно численному значению алгебраической суммы моментов всех сил,действующих на стержневую системус любой одной из сторон сечения, взятых относительно точки на оси сечения.

Составляющую, лежащую в сечении в данной площадке обознача­ется через и называется касательным напряжением.

Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Касательное напряжение можно разложить по координатным осям на две составляющие и (рис. в) Первый индекс при показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник