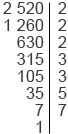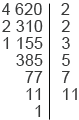Что называют наибольшим общим делителем натуральных чисел

Что называют наибольшим общим делителем натуральных чисел

Общим делителем натуральных чисел а и b называется такое натуральное число, на которое делятся оба числа а и b.

Наибольшим общим делителем чисел а и b называется наибольшее натуральное число, на которое делятся оба числа а и b.

Наибольший общий делитель чисел а и b обозначается НОД (а, b).

Пример: Пусть даны числа 16 и 24. Выпишем делители числа 16: 1, 2, 4, 8, 16.

Выпишем делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24.

Среди выписанных чисел есть одинаковые: 1, 2, 4, 8. Все эти числа называются общими делителями чисел 16 и 24. Наибольшее из них, число 8, называется наибольшим общим делителем чисел 16 и 24: НОД (16, 24) = 8.

Для любых заданных двух или более натуральных чисел можно найти наибольший общий делитель. Числа а и b называются взаимно простыми, если наибольший общий делитель этих чисел равен 1. Например, числа 14 и 35 взаимно простые.

Чтобы найти наибольший общий делитель двух чисел а и b, нужно:

Пример: Найти НОД (54, 90).

Решение. 54 = 2 · 3 3 ; 60 = 2 · 3 2 · 5.

Значит, НОД (54, 90) = 2 ·3 2 = 18.

Аналогично можно найти наибольший общий делитель трех и более чисел.

Если одно из двух чисел делится нацело на другое, то наибольший общий делитель этих чисел равен меньшему из них. Например, НОД (12, 36) = 12.

Наибольший общий делитель двух различных простых чисел равен единице.

Источник

Наибольший общий делитель (НОД), свойства и формулы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие наибольшего общего делителя

Начнем с самого начала и вспомним, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.

Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.

Если b — делитель целого числа a, которое не равно нулю, то модуль числа b не может быть больше модуля числа a. Значит любое число, не равное 0, имеет конечное число делителей.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).

Проверить результаты вычислений можно с помощью онлайн-калькулятора НОД и НОК.

Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.

Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.

Помимо НОД есть еще и НОК, что расшифровывается, как наименьшее общее кратное и означает наименьшее число, которое делится на каждое из исходных чисел без остатка.

Еще один пример. Рассчитаем НОД для 28 и 64.

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Свойства наибольшего общего делителя

У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.

Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.

Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.

Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.

Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.

Доказательство

Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.

Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.

В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.

Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.

Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.

Доказательство

Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.

Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.

Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).

Доказательство

Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.

Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.

Способы нахождения наибольшего общего делителя

Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.

1. Разложение на множители

Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.

Пример 1. Найти НОД (84, 90).

Ответ: НОД (84, 90) = 6.

Пример 2. Найти НОД (15, 28).

Ответ: НОД (15, 28) = 1.

Пример 3. Найти НОД для 24 и 18.

Ответ: НОД (24, 18) = 6

2. Алгоритм Евклида

Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.

Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.

Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.

Пример 1. Найти НОД для 24 и 8.

Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.

В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:

Пример 2. Найти наибольший общий делитель чисел 140 и 96:

Последний делитель равен 4 — это значит: НОД (140, 96) = 4.

Ответ: НОД (140, 96) = 4

Пошаговое деление можно записать столбиком:

Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:

Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.

Источник

Наибольший общий делитель

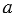
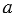
Наибольший общий делитель чисел и обозначают так: НОД(; ), то есть мы можем записать НОД(36; 126) = 18.

Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.

240 = 2222 3 5 165 = 3 5 11.

Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.

Найдем НОД(2520; 4620).

2 520 = 2 2 2 3 3 5 7 4 620 = 2 2 3 5 7 11.

Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357 рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.

Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).

Таким же образом можно найти НОД трех и более чисел.

Чтобы найти НОД нескольких натуральных чисел, надо:

Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.

Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:

2 520 = 2 3 3 2 5 1 7 1

Тогда НОД мы можем найти по следующему правилу:

Найдем НОД(2520; 4620):

Поделись с друзьями в социальных сетях:

Источник

Наибольший общий делитель НОД.

Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.

— число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;

— число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.

Кратко наибольший общий делитель чисел a и b записывают так:

Пример: НОД (12; 36) = 12.

Делители чисел в записи решения обозначают большой буквой «Д».

Наибольший общий делитель (НОД), свойства.

Это означает, в частности, что для приведения дроби к несократимому виду надо разделить её числитель и знаменатель на их НОД.

и поэтому представим в виде линейной комбинации чисел m и n:

.

Вычисление наибольшего общего делителя (НОД).

Эффективными способами вычисления НОД двух чисел являются алгоритм Евклида и бинарный алгоритм. Кроме того, значение НОД (m,n) можно легко вычислить, если известно каноническое разложение чисел m и n на простые множители:

где — различные простые числа, а и — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОД (m,n) и НОК(m,n) выражаются формулами:

Если чисел более двух: , их НОД находится по следующему алгоритму:

— это и есть искомый НОД.

Также, для того, чтобы найти наибольший общий делитель, можно разложить каждое из заданных чисел на простые множители. Потом выписать отдельно только те множители, которые входят во все заданные числа. Потом перемножаем между собой выписанные числа – результат перемножения и есть наибольший общий делитель.

Разберем пошагово вычисление наибольшего общего делителя:

1. Разложить делители чисел на простые множители:

2. Подчёркиваем одинаковые простые множители в обоих числах:

64 = 2 • 2 • 2 • 2 • 2 • 2

3. Находим произведение одинаковых простых множителей и записываем ответ:

НОД (28; 64) = 2 • 2 = 4

Ответ: НОД (28; 64) = 4

Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».

Первый способ записи НОД:

НОД (48; 36) = 2 • 2 • 3 = 12

Второй способ записи НОД:

Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15.

Источник

Наибольший общий делитель НОД.

Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.

— число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;

— число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.

Кратко наибольший общий делитель чисел a и b записывают так:

Пример: НОД (12; 36) = 12.

Делители чисел в записи решения обозначают большой буквой «Д».

Наибольший общий делитель (НОД), свойства.

Это означает, в частности, что для приведения дроби к несократимому виду надо разделить её числитель и знаменатель на их НОД.

и поэтому представим в виде линейной комбинации чисел m и n:

.

Вычисление наибольшего общего делителя (НОД).

Эффективными способами вычисления НОД двух чисел являются алгоритм Евклида и бинарный алгоритм. Кроме того, значение НОД (m,n) можно легко вычислить, если известно каноническое разложение чисел m и n на простые множители:

где — различные простые числа, а и — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОД (m,n) и НОК(m,n) выражаются формулами:

Если чисел более двух: , их НОД находится по следующему алгоритму:

— это и есть искомый НОД.

Также, для того, чтобы найти наибольший общий делитель, можно разложить каждое из заданных чисел на простые множители. Потом выписать отдельно только те множители, которые входят во все заданные числа. Потом перемножаем между собой выписанные числа – результат перемножения и есть наибольший общий делитель.

Разберем пошагово вычисление наибольшего общего делителя:

1. Разложить делители чисел на простые множители:

2. Подчёркиваем одинаковые простые множители в обоих числах:

64 = 2 • 2 • 2 • 2 • 2 • 2

3. Находим произведение одинаковых простых множителей и записываем ответ:

НОД (28; 64) = 2 • 2 = 4

Ответ: НОД (28; 64) = 4

Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».

Первый способ записи НОД:

НОД (48; 36) = 2 • 2 • 3 = 12

Второй способ записи НОД:

Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15.

Источник