Что называют модулем юнга
Модуль Юнга
Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела.
Это свойство любого материала, и оно зависит от температуры и оказываемого давления.
В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации.
Другими словами: когда тело деформируется, то появляется сила, которая стремится восстановить первоначальную форму и размер тела. Сила упругости является этой проявляющейся силой. Также она представляет собой следствие электромагнитного взаимодействия между частицами.
Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным.
Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.
Примеры значений модуля Юнга (упругости) для:
Таблица
Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи «гигапаскалей» ([ГПа]; ).
| Материал | Модуль Юнга E, [ГПа] |
|---|---|
| Алмаз | 1220 |
| Алюминий | 69 |
| Дерево | 10 |
| Кадмий | 50 |
| Латунь | 97 |
| Медь | 110 |
| Никель | 207 |
| Резина | 0,9 (≈ 1 МПа, мегапаскаль) |
| Сталь | 200 |
| Титан | 107 |
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):
Закон Гука (этот описывает явления в теле)
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.
Другие формулы вычисления модуля Юнга (модуля упругости)
Либо можно выразить k (жёсткость тела):
Пример решения задачи (через закон Гука):
Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.
Будем искать через закон Гука (σ = E × ε).
Помним из закона Гука:
σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)
ε = Δl/l (а это относительное удлинение, обозначается как ε)
Подставляем в формулу (σ = E × ε):
Например, в нашей таблице такой модуль Юнга имеет кадмий.
Модуль Юнга
Модуль Юнга рассчитывается следующим образом:
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
где 
Содержание
Значения модуля Юнга для некоторых материалов
Значения модуля Юнга для некоторых материалов приведены в таблице [2]
| Материал | модуль Юнга E, ГПа |
|---|---|
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Германий | 83 |
| Дюралюминий | 74 |
| Иридий | 520 |
| Кадмий | 50 |
| Кобальт | 210 |
| Константан | 163 |
| Кремний | 109 |
| Латунь | 95 |
| Лёд | 3 |
| Магний | 45 |
| Манганин | 124 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 210 |
| Стекло | 70 |
| Титан | 120 |
| Фарфор | 59 |
| Цинк | 120 |
| Хром | 300 |
Примечания
Примечания
См. также
Литература
Ссылки
Модуль объёмной упругости (





Полезное
Смотреть что такое «Модуль Юнга» в других словарях:
МОДУЛЬ ЮНГА — (модуль продольной упругости), отношение НАПРЯЖЕНИЯ, возникающего при растяжении тела, к удлинению, вызванному этим напряжением … Научно-технический энциклопедический словарь
модуль Юнга — Термин, используемый как синоним модуля упругости. Отношение растягивающих или сжимающих напряжений к конечной деформации. [http://www.manual steel.ru/eng a.html] Тематики металлургия в целом EN Young’s modulus … Справочник технического переводчика
модуль Юнга — [Young s modulus] назван по имени английского ученого Томаса Юнга; коэффициент пропорциональности Е, связывающий истинное (условное) напряжение δ (а) и истинную (условную) деформацию ε (Б) при одноосном деформировании в случае справедливости… … Энциклопедический словарь по металлургии
модуль Юнга — tampros modulis statusas T sritis Standartizacija ir metrologija apibrėžtis Statmenojo įtempio ir santykinės ilginės deformacijos dalmuo, t. y. E = σ/ε; čia σ – statmenasis įtempis, ε – santykinė ilginė deformacija. atitikmenys: angl. coefficient … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Модуль Юнга — Young s modulus Модуль Юнга. Термин, используемый как синоним модуля упругости. Отношение растягивающих или сжимающих напряжений к конечной деформации. См. также Modulus of elasticity Модуль упругости. (Источник: «Металлы и сплавы. Справочник.»… … Словарь металлургических терминов
модуль Юнга — tampros modulis statusas T sritis chemija apibrėžtis Įtempio ir santykinės deformacijos santykis. atitikmenys: angl. Young modulus; modulus of elasticity rus. модуль упругости; модуль Юнга ryšiai: sinonimas – Jungo modulis … Chemijos terminų aiškinamasis žodynas
модуль Юнга — Jungo modulis statusas T sritis fizika atitikmenys: angl. Yong’s modulus vok. Youngscher Modul, m rus. модуль Юнга, m pranc. module d’Young, m; module d’élasticité d’Young, m … Fizikos terminų žodynas
Модуль Юнга — то же что, модуль продольной упругости Е; см. Модули упругости … Большая советская энциклопедия
МОДУЛЬ ЮНГА — См. Модуль упругости грунта … Словарь по гидрогеологии и инженерной геологии
МОДУЛЬ ЮНГА-Е (МОДУЛЬ ПРОДОЛЬНОЙ УПРУГОСТИ ) — равен отношению нормального напряжения ρ к относительному удлинению ε, вызванному этим напряжением в направлении его действия E = ρ/ε; характеризует способность тел (г. п., м лов) сопротивляться деформация растяжения или… … Геологическая энциклопедия
Модуль Юнга (упругости) для стали и других материалов — определение, смысл
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Связь с другими модулями упругости
В случае изотропного тела модуль Юнга связан с модулем сдвига и модулем объёмной упругости соотношениями
где — коэффициент Пуассона.
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
Температурная зависимость модуля Юнга
где — адиабатический модуль упругости идеального кристалла при ; — дефект модуля, обусловленный тепловыми фононами; — дефект модуля, обусловленный тепловым движением электронов проводимости
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
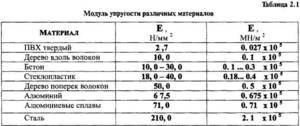
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.
Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Сталь и несколько разных её марок

Кстати, если не выражать все значения числовыми отношениями, а взять сразу и пос, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.
Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.
Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.
Модуль Юнга для стали и других материалов
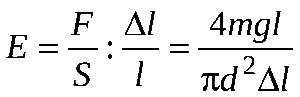
Описание и характеристики единицы измерения
Наименование величины степени жесткости было дано по имени его создателя — английского известного физика, который проводил исследования в области сжатия и растяжения различных жестких материалов, а также в процессах, которые проходят при механическом воздействии. О модуле Юнга справедливо упомянуть следующее:
А если совсем просто, то эта единица измерения просто показывает, насколько жесткий конкретный материал.
Буква Е является обозначением модуля Юнга. Согласно отечественной системе расчетов, измерение этой величины происходит в Паскалях. При этом Международная система единиц высчитывает эту величину в ньютонах, умноженных на метр в квадрате (СИ).
Модуль продольной жёсткости применяется при разного рода вычислениях во время проверки структур веществ на степень реакции при сжатии, растяжении, перегибании.
Следует отметить, что наибольшее количество конструкционных материалов, которые используют в таких расчетах, имеет довольно высокий показатель модуля Юнга. Чаще всего его значение начинается от отметки 109 Паскалей. В связи с этим в большинстве случаев для удобства записывания вычислений и самих расчетов применяют префикс «гига» (ГПа).
В задачах по динамике модуль Юнга воспринимается и учитывается в гораздо большем смысле, чем просто показатель жесткости. В этой области науки данное понятие рассматривается как гораздо более общий показатель — перечень возможностей стройматериалов и как среда прохождения процесса реакции их структуры на деформацию.
Показатели продольной эластичности
Для определенных конструкционных материалов, довольно часто используемых для достижения конкретных практических результатов, существуют уже выверенные показатели, сведенные в одну таблицу. В частности, от их параметров устойчивости к механическим воздействиям может зависеть срок службы строительных конструкций и прочих сооружений.
В соответствии с указанной таблицей, наивысший показатель модуля жесткости относится к стали, а наименьший — к древесным породам.

В таком случае физическое значение модуля продольной эластичности состоит в установлении математически точного отношения средних показателей напряжения к соответственным параметрам деформации на отдельно взятом отрезке диаграммы до конкретных, заранее установленных границ соразмерности.
Расчет поперечной жесткости
В форме точного выражения модуль Юнга рассчитывается таким способом: Е=q / е=tga.
Необходимо также упомянуть и о таком моменте, что модуль Юнга представляет собой еще и коэффициент пропорциональности и был применен в математическом описании закона Гука. Там великим ученым он был указан в таком математическом выражении: Q=Eе.
В связи с этим прямая связь модуля продольной эластичности с вымеряемыми параметрами поперечных разрезов материалов, которые участвуют в тестированиях на твердость, обнаруживается посредством таких выражений, как ЕА и Е1. При этом:
Таким образом, податливость материалов при растяжении свидетельствует о способности и самого материала, и изделия, выполненного из него, подвергаться линейному изгибанию. К примеру, при строительных работах это позволит более адекватно подобрать материал в зависимости от его назначения.
Из всего этого можно понять, что модуль Юнга представляет собой универсальную величину, благодаря которой появляется возможность разносторонне и с высокой точностью вычислять и охарактеризовывать качественные характеристики и параметры различных материалов.
Модуль Юнга и его основной физический смысл
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Показатели продольной эластичности
Для определенных конструкционных материалов, довольно часто используемых для достижения конкретных практических результатов, существуют уже выверенные показатели, сведенные в одну таблицу. В частности, от их параметров устойчивости к механическим воздействиям может зависеть срок службы строительных конструкций и прочих сооружений.
В соответствии с указанной таблицей, наивысший показатель модуля жесткости относится к стали, а наименьший — к древесным породам.
Цифровое установление модуля Юнга происходит с применением особой, специально рассчитанной диаграммы напряжения. Там указывается специфическая кривая, которая получается при множественных тестированиях каждого из отдельно взятых стройматериалов на устойчивость к механическим воздействиям.
Читать также: Как сплести из резинок хомячка
В таком случае физическое значение модуля продольной эластичности состоит в установлении математически точного отношения средних показателей напряжения к соответственным параметрам деформации на отдельно взятом отрезке диаграммы до конкретных, заранее установленных границ соразмерности.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Величину, обратную α, и называют модулем Юнга:
Отношение растягивающей силы F к S называют упругим напряжением σ:
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Модуль упругости меди — Справочник металлиста
Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки.
К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали.
Он же позволит на самой ранней стадии избежать появления этих проблем.
Модуль упругости (модуль Юнга) — это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения. Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях). Но инженеры на практике больше склоняются к применению размерности кгс/см2.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Модуль упругости
Стоит отметить, что эта величина непостоянная. Даже для одного материала она может иметь разное значение в зависимости от того, в какие точки была приложена сила.
Кое-какие пластично-упругие материалы имеют практически постоянное значение модуля упругости при работе как на растяжение, так и на сжатие: сталь, алюминий, медь.
А есть и такие ситуации, когда эта величина измеряется формой профиля.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Таблица модулей упругости сплавов
Если на изделие из определенного материала воздействовать некой силой, то он начинает сопротивляться этому действию: сжиматься, растягиваться или изгибаться. Способность к такому противостоянию можно оценить и выразить математически. Название этой прочностной характеристики – модуль упругости.
Параметр для каждого материала различный, и характеризует его прочность. Пользуются величиной при разработке конструкций, деталей и других изделий, с целью предотвращения нарушения их целостности.
Общее понятие
При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.
Определение модуля Юнга твердых тел
Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.
Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м 2 или по международной системе Па.
Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).
Опыт с пружинными весами
Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:
где ε – относительное удлинение или деформация.
Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм 2 или Н/м 2 :
Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.
В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.
Способы расчета модуля упругости
Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.
Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.
Обозначается как Е и выражается в Па или ГПа.
Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):
Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.
| Название материала | Значение параметра, ГПа |
| Алюминий | 70 |
| Дюралюминий | 74 |
| Железо | 180 |
| Латунь | 95 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 190/210 |
| Стекло | 70 |
| Титан | 112 |
| Хром | 300 |
Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.
Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:
где Fр – разрушающая сила, Н;
L – расстояние между опорами, мм;
b, h – ширина и толщина образца, мм;
ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.
При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.
Определение модуля упругости щебеночного основания
Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:
σ = 2με + λtrace(ε)I (7)
Оба параметра могут быть выражены из следующих соотношений:
Модуль упругости различных материалов
Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:
Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.
Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Инструмент для определения предела прочности
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.





