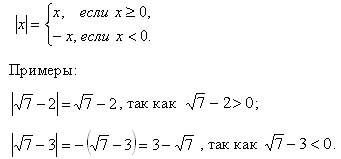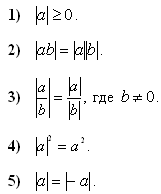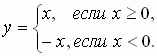Что называют модулем действительного числа

Числа. Модуль числа.

Модуль положительного действительного числа a – это само это число. Число в модуле:

Модуль отрицательного действительного числа а – это противоположное ему число:

В общем случае запись модуля числа выглядит так:

Модулем числа 5 будет 5, т.к. точка В(5) отстоит от начала отсчета на 5 единичных отрезков. Записывают так: |5| = 5.

Расстояние точки М(-6) от начала отсчета О соответствует 6 единичным отрезкам. Число 6 есть модуль числа -6. Записывают так: |-6| = 6.

Модуль числа бывает только положительным. Если рассматривать положительное число и нуль, то модуль их будет равен им же, а если рассматривать отрицательное число – то модуль равен противоположному числу. У противоположных чисел одинаковые модули:

Модуль нуля равен нулю, т.к. точка с координатой нуль совпадает с началом отсчета 0, то есть удалена от нее на 0 единичных отрезков:

Просмотрев определение модуля числа можно сделать вывод, что модуль числа соответствует числу под знаком модуля, не учитывая знак. Это утверждение поясняет из-за чего модуль числа иногда употребляется под значением абсолютной величины числа. Таким образом, модуль числа и абсолютная величина числа – это тоже самое.

К примеру, модуль целого числа −7 можно записать как ; модуль рационального числа 4,125 записывается как , а модуль иррационального числа имеет запись вида .

Источник

Абсолютная величина. Модуль.

Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).

Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.

Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:

Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:

Абсолютные величины, виды:

Свойства модуля.

.

Так как частное = , то . В силу предыдущего свойства имеем . Воспользуемся равенством , которое справедливо в силу определения модуля числа.

Основные свойства абсолютной величины.

Вещественные числа.

Комплексные числа.

Алгебраические свойства абсолютной величины.

Для каждого имеют место следующие соотношения:

Как для вещественных, так и для комплексных a, b имеют место соотношения:

Источник

Урок 29 Бесплатно Модуль числа

Обратите внимание на картинку.

Для того чтобы узнать тему нашего урока, попробуйте отгадать ребус.

На этом уроке разберемся, что называют модулем числа, раскроем его геометрический смысл, рассмотрим основные свойства модуля, научимся находить модуль числа и применять эти знания при решении задач.

Модуль числа (абсолютная величина)

В переводе с латинского «модуль» (modulus) означает мера, размер.

Считается, что данный термин впервые ввел в пользование английский философ и математик Роджер Котс, друг и ученик Исаака Ньютона.

Многие ученые использовали в своих научных трудах понятие модуль, однако символьное обозначение он приобрел только в конце XIX века.

В 1841 году выдающийся немецкий ученый Карл Теодор Вильгельм Вейерштрасс ввел символьное обозначение модуля числа, которое используют и применяют по сегодняшний день.

В некоторых случаях вместо «модуль числа» говорят: «абсолютная величина», но надо понимать, что это тождественно равные понятия.

У меня есть дополнительная информация к этой части урока!

Понятие «модуль» используется во многих областях деятельности человека.

Можно сказать, что квартира- это модуль дома, а бетонный блок- модуль здания.

Применение модуля придает строениям, сооружениям и их отдельным частям соизмеримость, единообразную форму, координацию размеров частей здания и комплекса в целом; облегчает установление норм и правил по строительству.

В космонавтике модуль- это автономная управляемая часть космического корабля (например, стыковочный модуль, орбитальный модуль и т.п.).

В радиоэлектронике модуль- это автоматизированный блок, функционально законченный узел радиоэлектронной аппаратуры.

В точных науках и технике модуль служит для названия некоторых коэффициентов и величин (например, модуль упругости, модуль сдвига, модуль сопротивления и другое).

В издательском деле модуль- это шаг сетки, основа расположения полос и разворотов в модульной системе верстки.

В судостроении все более широкое применение находит модульное строение судов и плавучих сооружений.

Блоки секций или блоки судна- типовые повторяющие блоки, так называемые модули, составляют корпус судна.

В программировании модули- это законченные самостоятельные фрагменты программы. Разделение программы на небольшие части- модули, позволяют облегчить программу, так как модуль можно применять повторно, его легче отладить и написать, повышает качество программного кода.

В общем говоря, под модулем часто понимают и представляют исходную единицу измерения, составную часть, служащую мерилом, или самостоятельную часть некоторой системы, часть конструкции

В математике модуль имеет несколько значений. Разберем, что в математике называют модулем числа (абсолютной величиной).

Рассмотрим понятие модуль с геометрической точки зрения.

Вам уже известно, что на координатной прямой мы отмечаем действительные числа, а каждому действительному числу на этой прямой соответствует определенная точка и наоборот, каждой точке на координатной прямой соответствует действительное число.

Точка задается некоторым расстоянием от начала координат.

Длина отрезка от начала координат до точки вмещает в себя определенное количество единичных отрезков координатной прямой.

Длина такого отрезка всегда неотрицательная величина.

Два мяча катнули по одной прямой. Первый мяч откатился вправо от исходной точки на 4 м, второй мяч влево от исходной точки на 6 м.

Изобразим координатную прямую и отметим на ней координаты точек остановки этих двух мячей.

Точка О— это исходная точка мячей- точка начала отсчета.

Единичный отрезок координатной прямой равен 1 деление- 1 метр.

Вправо откладываем координату первого мяча А (+4)

Влево откладываем координату второго мяча В (-6)

Расстояние от точки А до начала отсчета 4 единичных отрезка.

Длина ОА = 4 единичных отрезка.

Расстояние от точки В до начала отсчета 6 единичных отрезков.

Длина ОВ = 6 единичных отрезков.

Расстояние ОА и ОВ называют абсолютной величиной, модулем числа, они всегда положительны.

Таким образом, модулем числа называют расстояние на координатной прямой от начала отсчета до заданной точки (выраженной в единичных отрезках).

Обозначается модуль двумя вертикальными чертами слева и справа от числа | |.

Запись |A| читается как «Модуль А» или «Модуль числа А».

Пример 1

|7|— модуль числа 7

Изобразим координатную прямую, отметим на ней точку с координатой 7

Значит, модуль числа 7 равен самому числу 7

|7| = 7

Пример 2

Изобразим координатную прямую, отметим на ней точку с координатой (-5).

Зная определение модуля числа, мы можем утверждать, что от точки с координатой (-5) до точки начала отсчета О помещается 5 единичных отрезков.

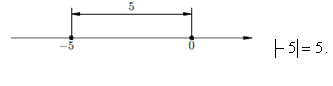
Значит, модуль числа (-5) равен 5

|-5| = 5

Пример 3

|-1|— модуль числа (-1)

В расстояние от точки с координатой (-1) до точки начала отсчета помещается только один единичный отрезок этой прямой, поэтому модуль (-1) равен 1.

|-1| = 1

Пройти тест и получить оценку можно после входа или регистрации

Свойства модуля (абсолютной величины)

Рассмотрим некоторые свойства модуля числа.

1. Модуль нуля равен нулю

Так как от нуля до начала отсчета нет никакого расстояния (0 единичных отрезков), модуль нуля и есть нуль.

|0| = 0

2. Модуль числа всегда число неотрицательное (т.е. положительное или нуль)

Мяч катнули вдоль прямой на расстояние, равное 3 м вправо, мяч ударился о стену и покатился вдоль прямой в обратном направлении на 3 м и остановился.

Изобразим на координатной прямой координаты точек в момент каждой остановки мяча.

Точка О на координатной прямой- это точка откуда катнули мяч- точка начала отсчета.

Единичный отрезок координатной прямой равен 1 деление- 1метр.

Можно ли утверждать, что мяч не преодолевал никакого расстояния, оставаясь в исходной точке в состоянии покоя, ведь в конечном счете мяч оказался в точке 0 м (от точки ноль до начала отсчета О не помещается ни одного единичного отрезка)? Конечно же, нет!

Путь мяча был бы равен нулю, если бы его вообще никуда не пинали, и он оставался в состоянии покоя в точке О.

Но мы должны понимать, что путь (расстояние), которое преодолел мяч, состоит из 3 единичных отрезков в правую сторону и 3 единичных отрезков в левую сторону; сложив все единичные отрезки, получим:

3 единичных отрезка + 3 единичных отрезка = 6 единичных отрезков

6 единичных отрезков = 6 м

Для определения пути мы складывали только числовое значение без учета направления. Это числовое значение и есть модуль числа.

Таким образом, можно сказать, что любое число состоит из знака и абсолютного значения (модуля).

Поэтому, чтобы найти модуль числа, нужно записать это число без учета знака.

У меня есть дополнительная информация к этой части урока!

В математике для лучшего восприятия темы «Модуль числа» придумали шуточную ассоциацию.

Заходя в баню (оказываясь под знаком модуль), отрицательное число моется, освобождается от знака. Из бани (из под знака модуль) число выходит «чистым»- без знака «минус».

В такой бане могут «мыться» положительные, отрицательные числа и ноль.

3. Модули противоположных чисел равны

Рассмотрим на примере данное утверждение:

Пусть модуль х равен 4, получим равенство |x| = 4

Отметим на координатной прямой точки, которые удовлетворяют этому равенству:

Модул ь- это расстояние от начала отсчета до точки в единичных отрезках, равное в данном случае четырем.

Откладываем 4 единичных отрезка вправо, получаем точку с координатой 4

Но такое же количество единичных отрезков можно отложить влево, тогда получим точку с координатой (-4)

Получим на координатной прямой две точки, которые удовлетворяют условию |x| = 4

В данном примере значение х может быть равным:

х = 4

На координатной прямой противоположные числа, хоть и по разные стороны от точки начала отсчета, но находятся на равных расстояниях от этой точки, т.е. по модулю равны.

4. Модуль произведения двух чисел равен произведению модулей этих чисел

В буквенном выражении это можно записать так:

5. Квадрат модуля числа равен квадрату этого числа

6. Модуль частного двух чисел равен частному их модулей

\(\mathbf<\Bigl| \frac\Bigr| = \frac<|x|> <|y|>, y \neq 0>\)(так как на нуль делить нельзя).

Пройти тест и получить оценку можно после входа или регистрации

Решение задач с применением модуля числа

Рассмотрим несколько примеров таких задач.

Задача 1

Запишите все числа, имеющие модуль 142.

Решение:

Представим координатную прямую с началом отсчета в точке О

142 единичных отрезка мы можем отложить на координатной прямой вправо и получим точку с координатой 142.

Также 142 единичных отрезка мы можем отложить влево от нуля, в этом случае получаем точку с координатой 142.

На координатной прямой находятся два числа, которые имеют модуль 142, а расстояние до этих точек содержат по 142 единичных отрезка.

|142| = 142

|-142| = 142

Задача 2

Решение:

Для этого найдем модули каждого из них:

|-15| = 15

|-1| = 1

|4| = 4

|7| = 7

Модули чисел получились: 15, 1, 4, 7

Расположим эти числа в порядке возрастания (от самого маленького к самому большому):

1, 4, 7, 15.

Получаем такую последовательность равенств,

|-1| = 1

|4| = 4

|7| = 7

|-15| = 15

Следовательно, числа в порядке возрастания их модулей должны располагаться так: -1, 4, 7, -15

Задача 3

На координатной прямой отметили две точки -73 и 68. Модуль какого числа больше?

Решение:

Представим, что на координатной прямой на определенном расстоянии от точки О (налала отсчета) отмечены две точки.

Слева от точки начала отсчета расположена точка с координатой -73

Справа от точки начала отсчета расположена точка с координатой 68

Расстояние от точки О до точки с координатой -73 содержит больше единичных отрезков, чем расстояние от точки О до точки с координатой 68 (т.е. координата точки -73 находится дальше от начала координат, чем точка с координатой 68).

Значит, модуль числа -73 больше модуля числа 68

|-73| = 73

|68| = 68

73 > 68, а это значит:

|-73| > |68|

Ответ: |-73| > |68|

Задача 4

Чему равны координаты этих точек?

Чему равен модуль каждой координаты?

Решение:

Построим координатную прямую, за начала отсчета примем точку О

Единичный отрезок равен 1 деление- 1 единица.

На координатной прямой отметим точки А и В

Точка А имеет координату A (-2), так как она отодвинута влево от точки О на расстояние в два единичных отрезка.

Точка В имеет координату В (6), так как она отодвинута вправо от точки О на расстояние в шесть единичных отрезков.

Получили точки с координатами A (-2) и В (6)

Модуль-это расстояние в единичных отрезках от заданной точки до начала отсчета.

|-2| = 2

Модуль 6 равен 6

|6| = 6

Ответ: Модули координат точек A (-2) и В (6) равны 2 и 6 соответственно.

Наверное, вы уже заметили, что значение координат может быть положительным и отрицательным, а модули только положительными.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Модуль действительного числа

Просмотр содержимого документа
«Модуль действительного числа»

Тема урока: Модуль действительного числа

Цели и задачи урока: Ввести определение модуля действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля;

Ввести функцию 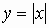, показать правила построения ее графика;

Научить разными способами решать уравнения, содержащие модуль;

Развивать интерес к математике, самостоятельность, логическое мышление, математическую речь, прививать аккуратность и трудолюбие.

Тип урока: Урок изучения нового материала

Мультимедийный проектор. ОС, презентация.

1. Организационный момент

Здравствуйте ребята, присаживайтесь, пожалуйста. Учитель отмечает отсутствующих и проверяет готовность учащихся к уроку.

2. Постановка темы и целей урока

3. Объяснение нового материала

Ребята, вы уже встречались с понятием модуля, пользовались обозначением |a|. Раньше речь шла только о рациональных числах. Теперь надо ввести понятие модуля для любого действительного числа.

Каждому действительному числу соответствует единственная точка числовой прямой, и, наоборот, каждой точке числовой прямой соответствует единственное действительное число. Все основные свойства действий над рациональными числами сохраняются и для действительных чисел

Вводится понятие модуля действительного числа. (Слайд 2).

Определение. Модулем неотрицательного действительного числа x называют само это число: |x| = x ; модулем отрицательного действительного числа х называют противоположное число: |x| = – x

На практике используют различные свойства модулей, например. (Слайд 3):

Модуль числа – это расстояние от начала отсчета до данного числа (Слайд 4):

Числовая прямая есть геометрическая модель множества R действительных числе. Отметим на числовой прямой две точки: a и b (два действительных числа a и b), обозначим через p(a; b) расстояние между точками a и b:

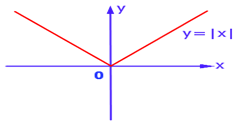
Задание 1. Построить график и перечислить свойства функции y = |x| (Слайды 5, 6).

1) Область определения – ( – ∞; + ∞).

2) у = 0 при х = 0; y 0 при x 0.

3) Функция непрерывная.

4) у_наим = 0 при х = 0, у_наиб не существует.

5) Функция ограничена снизу, не ограничена сверху.

6) Функция убывает на луче ( – ∞; 0) и возрастает на луче [0; + ∞).

7) Область значений функции – луч [0; + ∞).

Задание 2. Решить уравнение |x – 1| = 4. (Слайд 8):

– Ребята, какими способами можно решить уравнение?
– Аналитически, графически.

По определению модуля имеем:

– (х – 1) = 4,
х – 1 = – 4,
х = – 3.

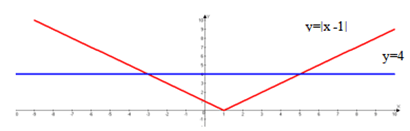
(Слайд 9) Построим на одной координатной плоскости графики функций y = |x – 1| и у = 4. Абсциссы точек пересечения графиков будут решениями уравнения.

Учитель: – Некоторые уравнения с модулем решаются проще с помощью геометрических соображений. (Слайд 10).

Уравнение |x – 1| = 4 можно прочитать так: нужно найти на числовой прямой такие точки, которые удалены от точки 1 на расстояние, равное 4.

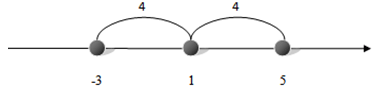
Рис. 4

4. Закрепление нового материала.

№ 16.2, №16.3, №16.4, №16.12, №16.16 (а,г), №16.19

5. Подведение итогов урока

6. Домашнее задание: прочитать материал §16, №16.6 16.11, 16.22

Список использованной литературы:

Звавич Л.И. Алгебра. Углубленное изучение. 8 кл.: задачник / Л.И. Звавич, А.Р. Рязановский. – 4-е изд., испр. – М.: Мнемозина, 2006. – 284 с.

Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений /А.Г. Мордкович. – 12-е изд., стер. – М.: Мнемозина, 2010. – 215 с.

Мордкович А.Г и др. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича. – 12-е изд., испр. и доп. – М.: Мнемозина, 2010. – 271 с.

Источник