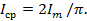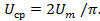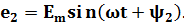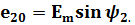Что называют мгновенным значением тока
Мгновенное значение



Мгновенное значение величины aзаписывается в виде:
где Аm – амплитуда (максимальное значение) величины;
ω – угловая частота, рад/с;
t – текущее значение времени, с;
Аргумент синуса (ωt +ψ) называется фазой. Угол ψ равен фазе в начальный момент времени t =0 и поэтому называется начальной фазой.
Угловая частота ω связана с периодом T и частотой f =1/Т формулами:
Частота f, равная числу колебаний в 1с., измеряется в герцах (Гц). При f=50 Гц имеем ω =314 рад/с.
Действующее и среднее значения синусоидальных токов и напряжений
Действующее значение синусоидального тока 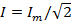
Аналогично существуют понятия действующих значений синусоидальных напряжений и ЭДС:
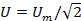
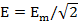
Действующее значение синусоидального тока часто называют среднеквадратичным или эффективным значениями.
Действующие значения токов и напряжений показывают большинство электроизмерительных приборов (амперметров, вольтметров).
В действующих значениях указываются номинальные токи и напряжения в паспортах различных электроприборов и устройств.
Под средним значением синусоидального тока понимают его среднее значение за половину периода:
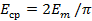
Элементы электрических цепей синусоидального тока
Основные элементы электрических цепей синусоидального тока:
-источники электрической энергии (источники ЭДС и источники тока);
-резистивные элементы (резисторы, реостаты, нагревательные элементы и т.д.);
-емкостные элементы (конденсаторы);
-индуктивные элементы (катушки индуктивности).
Резистивный элемент
По закону Ома напряжение на резистивном элементе:u=i⋅R=R⋅Im sinωt=Um sinωt, где Um =R⋅Im и ток i=Im sinωt.
1. Ток и напряжение в резистивном элементе совпадают по фазе (изменяются синфазно).
2. Закон Ома выполняется как для амплитудных значений тока и напряжения: Um =R⋅Im, так и для действующих значений тока и напряжения: U=R⋅I.
Выразим мгновенную мощность p через мгновенные значения тока i и напряжения u :
Что называют мгновенным значением тока
Переменным называется ток, который изменяется с течением времени:
Мгновенным значением переменного тока называется его значение в фиксированный момент времени.
Периодическим называют такой переменный ток, мгновенные значения которого повторяются через равные промежутки времени:
— период переменного тока, т.е. наименьший промежуток времени, по истечении которого мгновенные значения тока повторяются в той же последовательности.
Простейшим типом периодического тока является гармонический ток:
| где | — | амплитуда тока; |
| — | полная фаза колебания; | |
| — | начальная фаза колебания (при ); | |
| — | круговая частота (угловая скорость). |
Гармонический ток можно представить в виде проекции на вертикальную ось вращающегося вектора (рис.3.1).
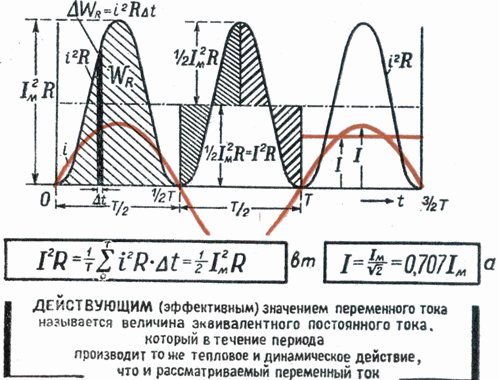
Действующим или эффективным значением гармонического тока называется значение такого постоянного тока, который протекая через одно и тоже неизменное сопротивление за период времени выделяет такое же количество тепла, что и рассматриваемый гармонический ток.
Между амплитудным и действующим значением гармонического тока существует простая связь:
Аналогично для напряжения и ЭДС:
Для мгновенных значений достаточно медленно изменяющихся переменных ЭДС и токов справедливы основные законы постоянного тока в их наиболее общей форме.
Основными элементами электрической цепи переменного тока являются активное сопротивление, индуктивность и ёмкость.
Активное сопротивление представляет собой элемент электрической цепи, в котором при прохождении тока происходит необратимый процесс преобразования электрической энергии в тепловую.
Численное значение активного сопротивления определяется отношением мощности, расходуемой на тепло к квадрату действующего значения переменного тока:
Необходимо помнить, что
В цепи переменного тока с активным сопротивлением ток и напряжение совпадают по фазе (рис.3.2).
Тогда на основании закона Ома для участка цепи без ЭДС:
Подставляя (1) в (2) получим:
Разность фаз между напряжением и током:
В цепи с активным сопротивлением мгновенные, амплитудные и действующие значения напряжения и тока связаны законом Ома:
В цепи переменного тока с индуктивностью напряжение опережает по фазе ток на (рис.3.3). Покажем это.
При прохождении переменного тока в индуктивности возникает ЭДС самоиндукции:
На основании закона Ома для участка цепи с ЭДС можно записать:
Разность фаз между напряжением и током:
Таким образом, в цепи переменного тока с индуктивностью амплитудные и действующие значения напряжения и тока формально связаны законом Ома:
В цепи переменного тока с ёмкостью напряжение отстаёт по фазе от тока на угол (рис.3.4). Докажем это.
Это напряжение приложено к конденсатору от внешнего источника. Оно уравновешивает ЭДС ёмкости (аналогичную ЭДС самоиндукции в катушке индуктивности), которая возникает при наличии зарядов на обкладках конденсатора.
На основании закона Ома для участка цепи с ЭДС можно записать:
За положительное направление тока в соответствии с законом сохранения электрического заряда принимается направление, при котором заряды покидают обкладки конденсатора:
Разность фаз между напряжением и током:
Это расчётная величина, которая не имеет физического смысла.
В общем случае в состав цепи переменного тока могут входить и активное сопротивление, и ёмкость, и индуктивность. Все эти элементы могут быть соединены между собой как последовательно, так и параллельно. На рисунке 3.5 показана схема последовательного соединения указанных элементов и соответствующая им векторная диаграмма для тока и напряжений.
Падение напряжения на элементах цепи:
Приложенное мгновенное значение напряжения равно сумме мгновенных падений напряжения на отдельных элементах цепи:
Сложение этих гармонических напряжений произведено в векторной форме (рис.3.5). Порядок построения векторной диаграммы обозначен цифрами.
— активная составляющая напряжения.
— реактивная составляющая напряжения.
Из векторной диаграммы следует, что
— полное сопротивление цепи;
— активная составляющая сопротивления цепи;
— реактивная составляющая сопротивления цепи.
В зависимости от знака реактивного сопротивления треугольники напряжений могут иметь вид:
Угол положителен при отстающем и отрицателен при опережающем токе.
Если все стороны треугольников напряжений (рис.3.7) разделить на амплитуду тока, то получатся соответствующие треугольники сопротивлений (рис.3.8).
Из треугольников сопротивлений (рис.3.8) следует ряд важных соотношений:
| где | — | активное сопротивление катушки индуктивности; |
| — | активное сопротивление конденсатора; | |
| — | активное сопротивление внешнего резистора. |
Состояние электрической цепи на частоте носит название резонанса напряжений.
Работа в цепи переменного тока за время одного периода выражается формулой:
Средняя за период мощность называется активной мощностью:
Она расходуется в активном сопротивлении цепи переменного тока.
Наряду с изложенным необходимо иметь в виду, что любая реальная катушка индуктивности как и любой реальный конденсатор при работе в цепи переменного тока имеют не только реактивные, но и активные сопротивления. На рисунке3.9 показаны реальные катушка индуктивности и конденсатор и их эквивалентные схемы:
Переменный электрический ток
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Термины AC и DC применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
i = I ampsin(ωt); u = U ampsin(ωt)
С учётом начальной фазы:
i = I ampsin(ωt + ψ); u = U ampsin(ωt + ψ)
Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.
Для синусоидального тока и напряжения амплитудой I amp (U amp) среднеквадратичное значение определится из расчёта:
Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой амплитудное, среднеквадратичное и средневыпрямленное значения.
Замечания и предложения принимаются и приветствуются!
Максимальное, мгновенное и действующее значение переменного тока и напряжения. Фаза и сдвиг фаз. Графическое изображение переменных величин.
Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.
Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Если ток изменяется по закону синуса, т. е.

то действующее значение переменного тока, обозначаемое также, как и значение постоянного тока заглавной буквой I латинского алфавита, определится как:
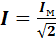
Аналогично для действующих значений синусоидальных напряжений:
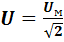
Фаза. Сдвиг фаз.
Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ. При вращении якоря в витках наводится ЭДС индукции одинаковой частоты ω и амплитуды Em, так как витки вращаются с одинаковой частотой в одном и том же магнитном поле.
Положение витков задано углами ψ1 и ψ2 для произвольного момента времени, которое можно считать t = 0. Мгновенные значения ЭДС как функции времени определяются выражениями:
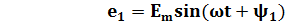
Следовательно, в момент t = 0 значения обеих этих ЭДС отличны от нуля:
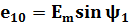
Электрические углы ψ1 и ψ2 характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.
Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
Действующие значения тока и напряжения

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время.
Величина I называется действующим значением переменного тока.
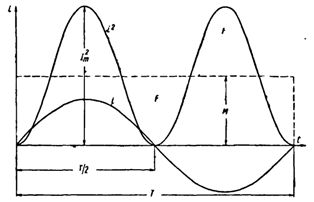
Среднее значение i2 при переменном токе определим следующим образом.
Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.
Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.
Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:
U = Um / √ 2 E= Em / √ 2
На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети: