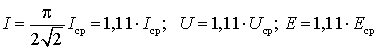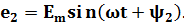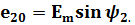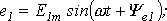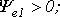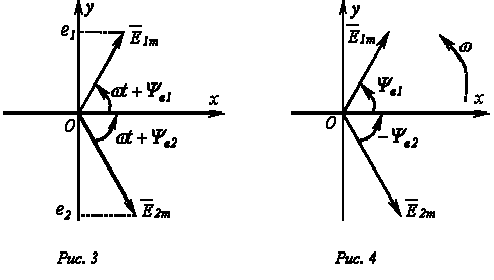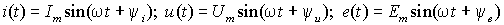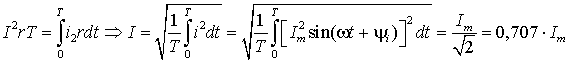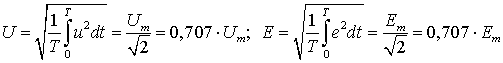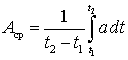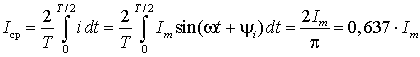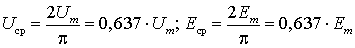Что называют мгновенным значением тока напряжения эдс
Что называют мгновенным значением тока напряжения эдс
Переменным называется ток, который изменяется с течением времени:
Мгновенным значением переменного тока называется его значение в фиксированный момент времени.
Периодическим называют такой переменный ток, мгновенные значения которого повторяются через равные промежутки времени:
— период переменного тока, т.е. наименьший промежуток времени, по истечении которого мгновенные значения тока повторяются в той же последовательности.
Простейшим типом периодического тока является гармонический ток:
| где | — | амплитуда тока; |
| — | полная фаза колебания; | |
| — | начальная фаза колебания (при ); | |
| — | круговая частота (угловая скорость). |
Гармонический ток можно представить в виде проекции на вертикальную ось вращающегося вектора (рис.3.1).
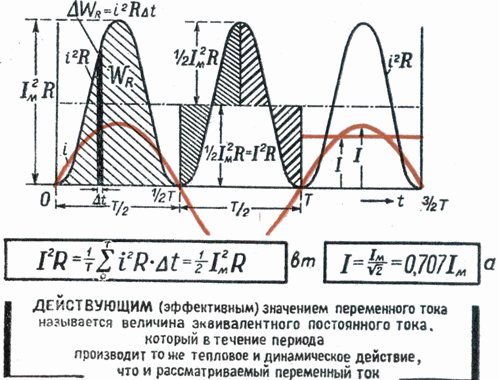
Действующим или эффективным значением гармонического тока называется значение такого постоянного тока, который протекая через одно и тоже неизменное сопротивление за период времени выделяет такое же количество тепла, что и рассматриваемый гармонический ток.
Между амплитудным и действующим значением гармонического тока существует простая связь:
Аналогично для напряжения и ЭДС:
Для мгновенных значений достаточно медленно изменяющихся переменных ЭДС и токов справедливы основные законы постоянного тока в их наиболее общей форме.
Основными элементами электрической цепи переменного тока являются активное сопротивление, индуктивность и ёмкость.
Активное сопротивление представляет собой элемент электрической цепи, в котором при прохождении тока происходит необратимый процесс преобразования электрической энергии в тепловую.
Численное значение активного сопротивления определяется отношением мощности, расходуемой на тепло к квадрату действующего значения переменного тока:
Необходимо помнить, что
В цепи переменного тока с активным сопротивлением ток и напряжение совпадают по фазе (рис.3.2).
Тогда на основании закона Ома для участка цепи без ЭДС:
Подставляя (1) в (2) получим:
Разность фаз между напряжением и током:
В цепи с активным сопротивлением мгновенные, амплитудные и действующие значения напряжения и тока связаны законом Ома:
В цепи переменного тока с индуктивностью напряжение опережает по фазе ток на (рис.3.3). Покажем это.
При прохождении переменного тока в индуктивности возникает ЭДС самоиндукции:
На основании закона Ома для участка цепи с ЭДС можно записать:
Разность фаз между напряжением и током:
Таким образом, в цепи переменного тока с индуктивностью амплитудные и действующие значения напряжения и тока формально связаны законом Ома:
В цепи переменного тока с ёмкостью напряжение отстаёт по фазе от тока на угол (рис.3.4). Докажем это.
Это напряжение приложено к конденсатору от внешнего источника. Оно уравновешивает ЭДС ёмкости (аналогичную ЭДС самоиндукции в катушке индуктивности), которая возникает при наличии зарядов на обкладках конденсатора.
На основании закона Ома для участка цепи с ЭДС можно записать:
За положительное направление тока в соответствии с законом сохранения электрического заряда принимается направление, при котором заряды покидают обкладки конденсатора:
Разность фаз между напряжением и током:
Это расчётная величина, которая не имеет физического смысла.
В общем случае в состав цепи переменного тока могут входить и активное сопротивление, и ёмкость, и индуктивность. Все эти элементы могут быть соединены между собой как последовательно, так и параллельно. На рисунке 3.5 показана схема последовательного соединения указанных элементов и соответствующая им векторная диаграмма для тока и напряжений.
Падение напряжения на элементах цепи:
Приложенное мгновенное значение напряжения равно сумме мгновенных падений напряжения на отдельных элементах цепи:
Сложение этих гармонических напряжений произведено в векторной форме (рис.3.5). Порядок построения векторной диаграммы обозначен цифрами.
— активная составляющая напряжения.
— реактивная составляющая напряжения.
Из векторной диаграммы следует, что
— полное сопротивление цепи;
— активная составляющая сопротивления цепи;
— реактивная составляющая сопротивления цепи.
В зависимости от знака реактивного сопротивления треугольники напряжений могут иметь вид:
Угол положителен при отстающем и отрицателен при опережающем токе.
Если все стороны треугольников напряжений (рис.3.7) разделить на амплитуду тока, то получатся соответствующие треугольники сопротивлений (рис.3.8).
Из треугольников сопротивлений (рис.3.8) следует ряд важных соотношений:
| где | — | активное сопротивление катушки индуктивности; |
| — | активное сопротивление конденсатора; | |
| — | активное сопротивление внешнего резистора. |
Состояние электрической цепи на частоте носит название резонанса напряжений.
Работа в цепи переменного тока за время одного периода выражается формулой:
Средняя за период мощность называется активной мощностью:
Она расходуется в активном сопротивлении цепи переменного тока.
Наряду с изложенным необходимо иметь в виду, что любая реальная катушка индуктивности как и любой реальный конденсатор при работе в цепи переменного тока имеют не только реактивные, но и активные сопротивления. На рисунке3.9 показаны реальные катушка индуктивности и конденсатор и их эквивалентные схемы:
Максимальное, мгновенное и действующее значение переменного тока и напряжения. Фаза и сдвиг фаз. Графическое изображение переменных величин.
Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.
Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Если ток изменяется по закону синуса, т. е.

то действующее значение переменного тока, обозначаемое также, как и значение постоянного тока заглавной буквой I латинского алфавита, определится как:
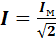
Аналогично для действующих значений синусоидальных напряжений:
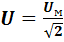
Фаза. Сдвиг фаз.
Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ. При вращении якоря в витках наводится ЭДС индукции одинаковой частоты ω и амплитуды Em, так как витки вращаются с одинаковой частотой в одном и том же магнитном поле.
Положение витков задано углами ψ1 и ψ2 для произвольного момента времени, которое можно считать t = 0. Мгновенные значения ЭДС как функции времени определяются выражениями:
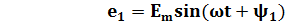
Следовательно, в момент t = 0 значения обеих этих ЭДС отличны от нуля:
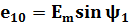
Электрические углы ψ1 и ψ2 характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.
Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
ДОМОСТРОЙСантехника и строительство
Дать определения. Мгновенное, амплитудное, действующее и среднее значения ЭДС, напряжения, тока.
Что ты хочешь узнать?
Ответ
Проверено экспертом
Речь идём о переменном токе.
Мгновенное значение (ЭДС или напряжения или тока) — значение величины в данный момент времени. обозначается чаще всего маленькими буквами: e, u,i.
Амплитудное значение (ЭДС или напряжения или тока) — максимальное значение. Обозначается :
Действующее значение отличается от максимального тем, что оно меньше максимального в раз, т.е.( на примере тока, для напряжения и ЭДС аналогично):
Обозначается действующее значение или без иднекса или с индексом «д»:
Смысл действующего значения: при переменном токе (i) за период выделиться столько же тепла, сколько выделиться при действующем значении
Имеено действующее значение показывают приборы, подключённые в цепь с переменным током.
Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.
Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Если ток изменяется по закону синуса, т. е.

то действующее значение переменного тока, обозначаемое также, как и значение постоянного тока заглавной буквой I латинского алфавита, определится как:
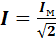
Аналогично для действующих значений синусоидальных напряжений:
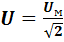
Фаза. Сдвиг фаз.
Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ. При вращении якоря в витках наводится ЭДС индукции одинаковой частоты ω и амплитуды Em, так как витки вращаются с одинаковой частотой в одном и том же магнитном поле.
Положение витков задано углами ψ1 и ψ2 для произвольного момента времени, которое можно считать t = 0. Мгновенные значения ЭДС как функции времени определяются выражениями:
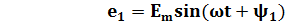
Следовательно, в момент t = 0 значения обеих этих ЭДС отличны от нуля:
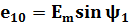
Электрические углы ψ1 и ψ2 характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.
Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
Дата добавления: 2016-05-25 ; просмотров: 7354 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
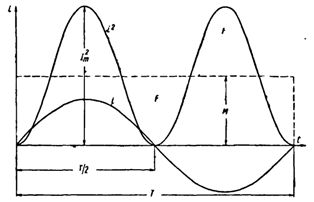
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
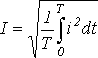
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2 соответствуют уравнения:
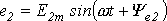
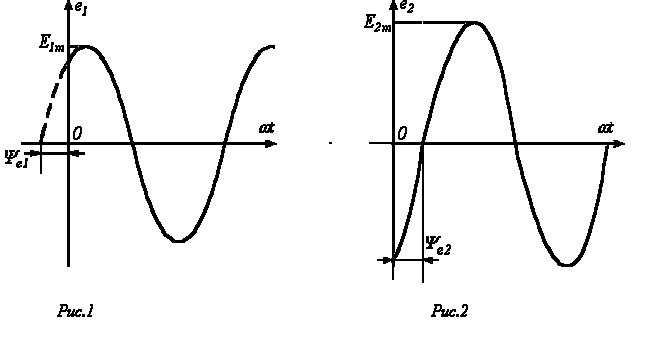
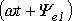
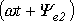
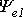
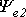
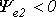
Величину 
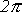
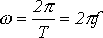
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
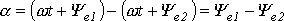
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
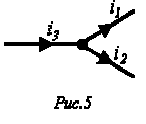
Пусть, например, в точке разветвления цепи (рис. 5) общий ток 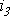
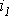
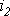
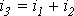
Каждый из этих токов синусоидален и может быть представлен уравнением
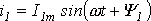
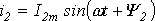
Результирующий ток также будет синусоидален:
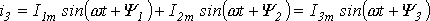
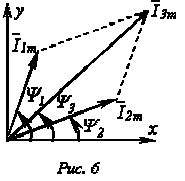
Определение амплитуды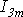

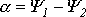
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
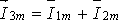
Построение векторной диаграммы в масштабе позволяет определить значения 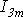

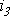
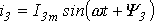
Действующие значения тока и напряжения

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время.
Величина I называется действующим значением переменного тока.
Среднее значение i2 при переменном токе определим следующим образом.
Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.
Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.
Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:
U = Um / √ 2 E= Em / √ 2
На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Что называют мгновенным значением тока напряжения эдс
В электрических цепях переменного тока ток, падение напряжения и ЭДС являются синусоидальными функциями времени –
где 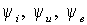
Для этих величин принят ряд соглашений по обозначениям, имеющим нормативную силу.
Мгновенные значения токов, напряжений и ЭДС следует обозначать строчными буквами в виде 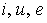
Максимальное значение или амплитуда обозначается соответствующей прописной буквой с индексом 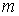
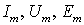
Помимо этих величин в цепях переменного тока широко используют т.н. действующие значения. Понятие действующего значения определяется из условия равенства теплового эффекта переменного и постоянного токов.
Пусть через некоторый участок электрической цепи с сопротивлением 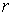
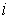
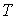
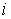
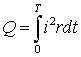
Обозначим через 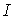
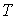
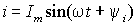
т.е. величина постоянного тока эквивалентного переменному току по количеству выделяемого тепла называется действующим или среднеквадратичным значением переменного тока. Как следует из полученного выражения, действующее и амплитудное значения синусоидального тока связаны между собой постоянным коэффициентом.
По аналогии с током действующие значения вводятся для напряжений и ЭДС
Действующие значения обозначаются прописными буквами без индекса.
Кроме действующих значений для синусоидальных величин иногда используются также средние значения. Под средним значением любой величины за интервал времени от t 1 до t 2 понимается
Но интеграл от синусоидальной функции за период равен нулю, поэтому для определения среднего значения используют интервал времени в половину периода. Тогда для тока получим:
Для напряжений и ЭДС средние значения определятся аналогично
Отсюда через максимальные значения можно найти соотношение между действующими и средними значениями