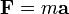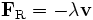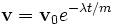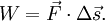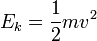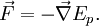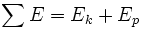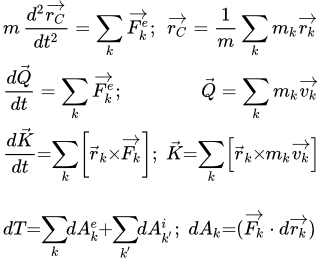Что называют механической системой

Презентация к защите

Механической системой или системой материальных точек называется совокупность точек, связанных между собой так, что движение каждой точки системы зависит от движения остальных точек системы.

Примером механической системы является всякое абсолютно твердое тело или же совокупность тел, связанных между собой.

Выбор механической системы зависит от нас, так как, изучая движение какого-либо механизма, можно в зависимости от характера поставленной задачи принять за механическую систему как весь механизм в целом, так и любое его звено.

В динамике различают изменяемые и неизменяемые системы точек.

Система называется неизменяемой, если точки ее не перемещаются относительно друг друга, изменяемой, если точки системы перемещаются относительно друг друга.

Всякое абсолютно твердое тело можно рассматривать как неизменяемую систему. Примером изменяемой системы являются деформируемое (не абсолютно твердое) тело.

Классификация сил, действующих на систему.

В динамике принято делить все силы, действующие на систему точек, на два вида: внутренние и внешние.

Внутренними называются силы, с которыми точки или тела, составляющие систему, действуют друг на друга.

Внешними называются силы, с которыми действуют на систему точки или тела, не входящие в состав самой системы.

Если деление сил на активные и реакции связи зависит от физической природы сил, то деление их на внешние и внутренние зависит от нашего выбора. Одна и та же сила может быть внешней по отношению к одной системе точки внутренней по отношению к другой. Таким образом, деление сил на внешние и внутренние является условным и зависит от того, что включим в состав системы.

Пример. Если рассмотреть движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней. Если же рассмотреть Землю как систему точек, то эта сила станет внешней.

Свойства внутренних сил системы

1. Геометрическая сумма всех внутренних сил системы равна нулю, то есть

Действительно, на основании третьего закона динамики силы, с которыми действуют друг на друга точки системы, равны по величине и противоположны по направлению (рис.1).

Складывая такие силы, получаем:

потому что и — коллинеарны.

Полученные выводы упрощают исследования вопросов, относящихся к системе точек, так как они позволяют в некоторых случаях не принимать в расчет внутренние силы системы.

Центр масс системы

Когда система состоит из очень большого числа точек, то изучить ее движение сложно и даже иногда невозможно. В таких случаях рассматривается движение всей системы как одного целого. С этой целью и вводится понятие центра масс.

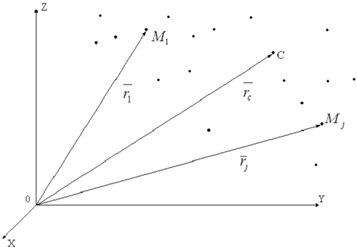
Из курса статики известно, что все эти силы можно заменить одной силой, приложенной в точке С, называемой центром параллельных сил. Координаты этой точки определяются по формулам:

Заменим Pj в формулах (1) его значением, координаты примут вид

где (масса всех точек системы), получим

Эти формулы (3) определяют точку С, положение которой уже не зависит от сил, действующих на систему, а зависит лишь от положения материальных точек системы и от их масс. Точка С и называется центром масс системы.

Следовательно, центром масс системы называется геометрическая точка С координаты которой определяются по формулам (3).

Положение точки С можно определить или ее координатами по формулам (3) или ее радиус-вектором по формуле (4).

Примечание. В поле силы тяжести центр масс системы совпадает с ее центром тяжести (для неизменяемой системы). Но, если центр тяжести существует только для неизменяемой системы, находящейся в поле тяжести, то центр масс существует для любой системы, находящейся в любом пространстве, и положение его не зависит от сил, действующих на систему. Таким образом, понятие центра масс и центра тяжести не являются тождественным понятиями. Центр тяжести является частным случаем по отношению к понятию центра масс.

Источник

iSopromat.ru

Под механической системой в механике понимается совокупность материальных точек (твердых тел), движения которых взаимосвязаны между собой.

Система материальных точек, движение которых не ограничено никакими связями, называется системой свободных материальных точек (примером являются планеты солнечной системы, движение которых по орбитам определяется действующими на них силами).

Определяющим признаком механической системы является наличие сил взаимодействия между отдельными материальными точками (телами) системы.

Действие связей на точки (элементы) механической системы выражается силами, называемыми реакциями связей. Поэтому все силы, действующие на систему несвободных точек, можно разделить на две группы: задаваемые (активные) силы и реакции связей. В то же время все силы, действующие на точки любой механической системы (свободной или несвободной), можно подразделить и по другому признаку: на внешние и внутренние силы.

Внешними называются силы, действующие на точки (тела) системы со стороны материальных точек (тел), не входящих в состав данной механической системы.

Внутренними называются силы взаимодействия между материальными точками (телами) данной механической системы.

Одна и та же сила может быть как внешней, так и внутренней, в зависимости от того, какая механическая система рассматривается. Так, например, реакции подшипников вала являются внешними силами относительно вала. Эти же реакции относятся к внутренним силам, когда рассматривается вся установка.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

Механическая система. Силы внешние и внутренние

Изучение данных вопросов необходимо для динамики колебательного движения механических систем, теории удара, для решения задач в дисциплинах «Сопротивление материалов» и «Детали машин».

Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.

В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.

Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Необходимость этой классификации сил выяснится в следующих главах.

Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.

Внутренние силы обладают следующими свойствами:

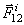
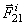
1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы (рис.31) действуют друг на друга с равными по модулю и противоположно направленными силами и , сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то

Источник

Механическая система

История…

Фундаментальные понятия
Пространство · Время · Масса · Сила Энергия · Импульс

Формулировки
Ньютоновская механика Лагранжева механика Гамильтонова механика

Разделы
Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика

Учёные
Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши

Класси́ческая меха́ника — вид механики (раздела физики, изучающей законы изменения положений тел и причины, это вызывающие), основанный на 3 законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «Ньютоновской механикой». Важное место в классической механике занимает существование инерциальных систем. Классическая механика подразделяется на кинематику (которая изучает геометрическое свойство движения без рассмотрения его причин), статику (которая рассматривает равновесие тел) и динамику (которая рассматривает движение тел).

Классическая механика дает очень точные результаты в рамках повседневного опыта. Но для систем, движущихся с большими скоростями, приближающимися к скорости света, более точные результаты дает релятивистская механика, для систем микроскопических размеров — квантовая механика, а для систем, обладающих обеими характеристиками — квантовая теория поля. Тем не менее, классическая механика сохраняет свое значение, поскольку (1) она намного проще в понимании и использовании, чем остальные теории, и (2) в обширном диапазоне она достаточно хорошо приближается к реальности. Классическую механику можно использовать для описания движения таких объектов, как волчок и бейсбольный мяч, многих астрономических объектов (таких, как планеты и галактики), и даже многих микроскопических объектов, таких как органические молекулы.

Хотя классическая механика в общих чертах совместима с другими «классическими теориями», такими как классическая электродинамика и термодинамика, в конце 19 века были найдены несоответствия, которые удалось разрешить только в рамках более современных физических теорий. В частности, классическая электродинамика предсказывает, что скорость света постоянна для всех наблюдателей, что трудно совместить с классической механикой, и что привело к необходимости создания специальной теории относительности. При рассмотрении совместно с классической термодинамикой, классическая механика приводит к парадоксу Гиббса в котором невозможно точно определить величину энтропии и к ультрафиолетовой катастрофе, в которой абсолютно чёрное тело должно излучать бесконечное количество энергии. Попытки разрешить эти проблемы привели к развитию квантовой механики.

Содержание

Описание теории

Перейдем к изложению основных понятий классической механики. Для простоты, мы будем рассматривать только материальную точку, т. е. тело, размером которого можно пренебречь. Движение материальной точки характеризуется несколькими параметрами: её положением, массой, и приложенными к ней силами. Рассмотрим каждый из них по очереди.

В действительности, любое тело, которое подчиняется законам классической механики, обязательно имеет ненулевой размер. Настоящие материальные точки, такие, как электрон, подчиняются законам квантовой механики. Тела ненулевого размера могут испытывать более сложные движения, поскольку может меняться их внутренняя конфигурация, например, потому что теннисный мяч может двигаться, вращаясь. Тем не менее, мы сможем применить к подобным телам результаты, полученные для материальных точек, рассматривая такие тела, как совокупности большого количества взаимодействующих материальных точек. Мы сможем показать, что такие сложные тела ведут себя, как материальные точки, при условии, что они малы в масштабах рассматриваемой задачи.

Радиус-вектор и его производные

Радиус-вектор материальной точки указывает на её положение по отношению к произвольной точке, зафиксированной в пространстве, которая обычно называется началом координат, и обозначается O. Это вектор r соединяющий начало координат с частицей. В общем случае, материальная точка движется, поэтому r является функцией t, промежутка времени прошедшего с произвольного начального момента. Скорость изменения положения со временем, определяется так:

.

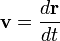
Ускорение, или скорость изменения скорости, это:

.

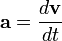
Вектор ускорения может меняться за счет изменения его направления, величины, или и того и другого. Если скорость уменьшается, иногда пользуются термином «замедление», но вообще, термин «ускорение» относится к любому изменению скорости.

Второй закон Ньютона

Второй закон Ньютона связывает массу и скорость частицы с векторной величиной, известной как сила. Пусть m — масса тела и F — векторная сумма всех приложенных к нему сил (то есть равнодействующая сила.) Тогда второй закон Ньютона выглядит так:

.

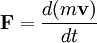
Величина mv называется импульсом. В большинстве случаев, масса m не изменяется со временем, и закон Ньютона можно записать в упрощенной форме

где a — ускорение, определенное выше. Не всегда выполняется условие независимости массы от времени. Например, масса ракеты уменьшается по мере использования горючего. В таких случаях последнее выражение неприменимо, и следует пользоваться полной формой второго закона Ньютона.

Второго закона Ньютона недостаточно для описания движения частицы. Дополнительно требуется описание силы F, полученное из рассмотрения сущности физического взаимодействия, в котором участвует тело. Например, сила трения может быть смоделирована как функция скорости частицы, а именно

где λ — некоторая положительная постоянная. Получив независимое выражение для каждой силы, действующей на тело, мы можем подставить его во второй закон Ньютона и получим дифференциальное уравнение, называемое уравнением движения. Продолжая наш пример, примем, что на тело действует только сила трения. Тогда уравнение движения будет иметь вид

.

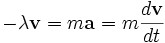
Это можно интегрировать, что даст

где v₀ — начальная скорость. Это означает, что скорость тела экспоненциально уменьшается со временем до нуля. Проинтегрировав последнее выражение, мы можем получить радиус-вектор r тела, как функцию времени.

Важными силами являются сила всемирного тяготения и сила Лоренца для электромагнетизма. Помимо этого, для определения сил, действующих на тело, используется третий закон Ньютона: если мы знаем, что тело A действует с силой F на тело B, значит B должно действовать с равной по величине и противоположной по направлению силой реакции, −F, на A.

Энергия

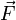
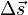
Если сила приложена к частице, которая перемещается на , то работа, совершенная силой, определяется как скалярное произведение силы и вектора перемещения:

Если масса частицы постоянна, а W_total полная работа, совершенная частицей, определяемая как сумма работ совершенных приложенными к частице силами, то второй закон Ньютона примет вид:

где E_k называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до скорости v :

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Если все силы, действующие на частицу консервативны, и E_p является полной потенциальной энергий, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

.

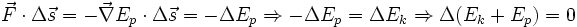Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

является постоянной относительно времени. Это очень полезно, потому что часто приходится сталкиваться с консервативными силами.

Источник

Динамика твердого тела и системы. Определения, законы, теоремы

Механическая система. Основные понятия

Свойства внутренних сил

Приводимые ниже свойства внутренних сил являются третьим законом Ньютона для системы материальных точек.

Свойство 1
Векторная сумма (главный вектор) всех внутренних сил системы равна нулю:
.

Свойство 2
Векторная сумма моментов всех внутренних сил системы, относительно произвольной точки O равена нулю:
.

Дифференциальные уравнения движения точек системы

Общие теоремы динамики механической системы

Общие теоремы динамики – это теорема о движении центра масс механической системы, теорема об изменении количества движения, теорема об изменении главного момента количества движения (кинетического момента) и теорема об изменении кинетической энергии механической системы.

Теорема о движении центра масс механической системы

Теорема о движении центра масс механической системы
Произведение массы системы на ускорение ее центра масс равно векторной сумме всех действующих на систему внешних сил:
.

Здесь – масса системы; – ускорение центра масс системы: ;
– скорость центра масс системы: ;
– радиус вектор (координаты) центра масс системы: ;
– координаты и массы точек, из которых состоит система.

Теорема об изменении количества движения (импульса)

Теорема об изменении количества движения в дифференциальной форме
Производная по времени от количества движения (импульса) системы равна векторной сумме всех действующих на систему внешних сил:
.

Теорема об изменении количества движения в интегральной форме
Изменение количества движения (импульса) системы за некоторый промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени:
.

Закон сохранения количества движения (импульса)
Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения.

Если сумма проекций внешних сил на какую-либо ось равна нулю, то проекция количества движения системы на эту ось будет постоянной.

Тело переменной массы. Движение ракеты

Уравнение Мещерского
Дифференциальное уравнение движения точки переменной массы называется уравнением Мещерского:
.
Здесь – масса тела, которая является функцией от времени t ; – векторная сумма приложенных к телу внешних сил; – скорость отделяющихся частиц относительно тела.

Реактивная сила направлена в сторону, противоположную истечению отделяющихся частиц (топлива), и определяется по формуле:
,
где – расход топлива (кг/с).

Формула Циолковского

Скорость v движения ракеты под действием одной только реактивной силы определяется по формуле Циолковского:
.
Здесь – начальная скорость ракеты; u – скорость истечения реактивных газов относительно ракеты; – масса сгоревшего топлива; – масса корпуса ракеты с остатками топлива. Когда топливо выгорает полностью, то – это масса корпуса ракеты с полезной нагрузкой.

Теорема об изменении главного момента количества движения (теорема моментов)

Теорема моментов в инерциальной системе координат

Если система состоит из нескольких частей, то главный момент количества движения системы равен сумме моментов количеств движения отдельных ее частей.

Выпишем компоненты уравнения (М2) в неподвижной системе координат Oxyz :
;
;
.

Закон сохранения главного момента количества движения (момента импульса)
Если сумма моментов всех приложенных к системе внешних сил относительно данного неподвижного центра O равна нулю, то главный момент количества движения системы относительно этого центра будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения:
.

Часто встречаются случаи, когда система вращается вокруг неподвижной оси. Тогда нужно спроектировать векторное уравнение (М2) на направление этой оси. В результате получим теорему моментов, применительно к вращению относительно оси.

Производная по времени от кинетического момента системы относительно некоторой неподвижной оси равна сумме моментов всех внешних сил системы относительно этой оси. Если сумма моментов всех приложенных к системе внешних сил относительно некоторой неподвижной оси равна нулю, то кинетический момент системы относительно этой оси будет постоянным.

Теорема моментов в системе координат, связанной с центром масс

Кинетический момент системы относительно неподвижного центра удобно использовать в тех задачах, в которых система имеет одну или несколько закрепленных точек. Например при вращении тела или системы тел вокруг точки или оси. Когда таких точек нет, то наиболее удобным в использовании является кинетический момент относительно центра масс в системе координат, в которой центр масс покоится, а оси остаются параллельными осям инерциальной системы отсчета. В общем случае, система отсчета, связанная с центром масс, не является инерциальной, но она не вращается относительно инерциальной системы отсчета.

В (М2) ⇑ мы использовали кинетический момент системы, вычисляемый относительно произвольной неподвижной точки в инерциальной системе отсчета. Уравнения для кинетического момента имеют тот же вид, если в качестве полюса взять центр масс C системы.

В (М5) мы используем неинерциальную систему координат, начало которой, в течении всего движения системы, находится в центре масс, а оси параллельны осям инерциальной системы координат. Естественно, что если мы выберем инерциальную систему координат, начало которой в данный момент времени совпадает с центром масс, то теорема моментов не изменит своего вида (М5). То есть центр масс обладает такой особенностью, что теорема моментов относительно него имеет одну и ту же форму, как в инерциальной системе отсчета, так и в неинерциальной системе, начало которой на всем протяжении движения совпадает с центром масс, а оси параллельны осям инерциальной системы отсчета. Такая особенность возникает только для центра масс системы. Для других точек, уравнение моментов в неинерциальной системе отсчета не имеет вида (М5).

Кинетический момент твердого тела

Здесь мы выбрали в качестве полюса неподвижную (в рассматриваемый момент времени) точку. Если, в качестве полюса выбрать центр масс тела, то компоненты момента импульса определяются по аналогичной формуле:
.
Для других точек, момент импульса выражается через угловую скорость более сложным образом.

Теорема об изменении кинетической энергии

Кинетической энергия системы

Если система состоит из нескольких тел, то кинетическая энергия системы равна сумме кинетических энергий тел, составляющих систему.

Работа сил и мощность

Все сказанное в отношении работы и потенциальной энергии в разделе «Динамика материальной точки», имеет место и для динамики системы тел.
См. Работа силы. Мощность Силовые поля и потенциальная энергия
Единственное отличие заключается в том, что там силы приложены только к одной исследуемой точке. Для системы, внешние силы могут быть приложены к разным точкам, составляющих систему. При этом одна сила приложена только к одной точке, но этих сил может быть много. Точку, к которой приложена сила называют точкой приложения силы.

При рассмотрении твердых тел, мы можем упростить реальную систему сил, воспользовавшись результатами статики. Для этого нужно преобразовать сложную систему реальных сил на эквивалентную ей, более простую, систему. Так например, систему сил тяжести, действующих на каждую точку тела, можно заменить одной равнодействующей силой, приложенной к центру масс тела. Тогда все вычисления можно выполнять только для одной силы с точкой приложения в центре масс тела.

Работа при перемещении точки

Мощность равна скалярному произведению векторов силы и скорости:
.

Работа при движении тела

Если тело движется поступательно, то скорости и перемещения всех его точек равны. В этом случае, работа и мощность вычисляются также как и при перемещении точки. Этот случай рассмотрен выше.

Теорема об изменении кинетической энергии системы

Теорема об изменении кинетической энергии системы в дифференциальной форме.
Дифференциал (приращение) кинетической энергии системы при некотором ее перемещении равно сумме дифференциалов работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.

Теорема об изменении кинетической энергии системы в интегральной форме.
Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.

Неизменяемая система – это механическая система, в которой расстояние между любыми двумя взаимодействующими точками остается постоянным во все время движения.
Идеальные связи – это связи, для которых сумма элементарных работ их реакций на любом возможном перемещении системы равна нулю.

Коэффициент полезного действия

В машинах и механизмах, совершающих некоторую полезную работу, силы можно разделить на следующие виды.

Пусть N_маш – полезная мощность машины; N_дв – мощность двигателя. Тогда
.

Закон сохранения полной механической энергии

Если система движется под действием потенциальных сил, то сумма кинетической T и потенциальной Π энергий сохраняет постоянное значение:
.

Механическая энергия – это сумма кинетической и потенциальной энергии.

Уменьшение механической энергии, как правило, связано с ее превращением в тепловую, электрическую, электромагнитную энергию, энергию звука и электромагнитных колебаний (свет, электромагнитные волны). Увеличение механической энергии связано с обратными процессами превращения различных видов энергии в механическую.

Геометрия масс

Моменты и тензор инерции твердого тела

В этом разделе мы рассматриваем величины, характеризующие распределение массы системы в пространстве.

Сложившаяся система обозначений

Тензор инерции твердого тела

Тензор инерции имеет следующие шесть компонент:
;
;
.
Если в качестве полюса O выбрать центр масс C тела, то компоненты момента импульса и кинетическая энергия тела T вычисляются по относительно простым формулам:
.
Здесь – скорость центра масс тела, – компоненты угловой скорости.

Моменты инерции твердого тела

Определения моментов инерции

Свойства моментов инерции

Сумма осевых моментов инерции

Знаки моментов инерции
Осевые моменты инерции не могут быть отрицательными:
.
Центробежные моменты инерции могут быть положительными, отрицательными, или равными нулю.

Симметричность моментов инерции
Центробежные моменты инерции симметричны относительно своих индексов:
.

Все моменты инерции имеют размерность [кг·м 2 ].

Моменты инерции в разных системах координат

Повороты системы координат

Любое тело в пространстве имеет три главные оси инерции и три значения главных моментов инерции (относительно предварительно выбранной точки O ). При этом главные моменты инерции могут иметь равные значения.
Стоит подчеркнуть, что главные оси определяются относительно определенной точки тела. При выборе другой точки, главные оси могут иметь другие направления.

Тело с плоскостью симметрии
Если распределение массы тела в пространстве имеет плоскость симметрии, то любая ось, перпендикулярная к этой плоскости, будет главной осью инерции тела, а две другие главные оси лежат в плоскости симметрии.

Тело с осью симметрии
Если распределение массы тела в пространстве имеет ось симметрии, то эта ось является главной центральной осью инерции.

Параллельность главных осей
Если точка O расположена на главной центральной оси тела, то главные оси, проходящие через эту точку, параллельны главным центральным осям.

Главная ось, не проходящая через центр масс
Главная ось инерции, не проходящая через центр масс тела, является главной осью инерции только в одной точке.

По этой причине, величина полярного момента инерции не зависит от поворотов системы координат. То есть является инвариантом относительно поворотов системы координат. Она зависит от выбранного центра, относительно которого определяются моменты инерции.

Момент инерции относительно произвольной оси

Перенос системы координат. Теорема Гюйгенса-Штейнера

Отсюда следует, что осевой момент инерции будет иметь наименьшее значение относительно той оси, которая проходит через центр масс тела.

Моменты инерции некоторых тел

Однородный стержень

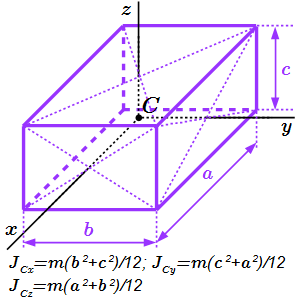
Прямоугольный параллелепипед

Рассмотрим прямоугольный параллелепипед с длинами ребер a, b, c (см. рисунок). Его центр масс C находится в центре параллелепипеда. Оси, проведенные через центр масс параллельно сторонам, будут главными центральными осями инерции. Моменты инерции прямоугольного параллелепипеда:

.

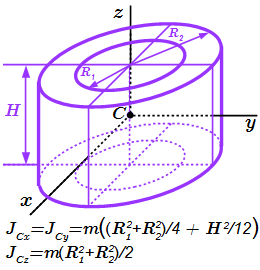
Полый цилиндр

Однородный сплошной диск

Тонкий обруч

Динамика твердого тела

Свободное движение твердого тела

Поступательное движение твердого тела

Плоское движение твердого тела

Вращение твердого тела вокруг неподвижной оси

Физический и математический маятники

Далее мы будем приводить данные только для плоского движения маятника. То есть мы считаем, что маятник совершает колебания вокруг неподвижной оси.

Математический маятник – это материальная точка, подвешенная на нерастяжимой невесомой нити, и совершающая колебания под действием силы тяжести. 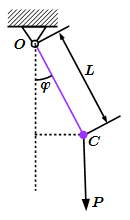Математический маятник.

Приведенная длина физического маятника – это длина математического маятника, частота колебаний которого совпадает с частотой колебаний рассматриваемого физического маятника.
Центром качаний физического маятника называется точка K на оси физического маятника, находящаяся на расстоянии его приведенной длины от точки подвеса.

Положение центра качания
Центр качаний всегда расположен ниже центра масс:
.

Принцип Даламбера

Суть принципа Даламбера состоит в том, чтобы задачи динамики свести к задачам статики. Для этого предполагают (или это заранее известно), что тела системы имеют определенные (угловые) ускорения. Далее вводят силы инерции и (или) моменты сил инерции, которые равны по величине и обратные по направлению силам и моментам сил, которые по законам механики создавали бы заданные ускорения или угловые ускорения

Принцип Даламбера
Если в любой момент времени к каждой точке системы приложить силы инерции и реально действующие силы, то полученная система сил будет находиться в равновесии, и к ней можно применять уравнения статики.

Принцип возможных перемещений

Принцип возможных перемещений применяется для решений задач статики. В некоторых задачах, он дает более короткое решение, чем составление уравнений равновесия. Особенно это касается систем со связями (например, системы тел, соединенные нитями и блоками), состоящих из множества тел

Принцип возможных перемещений.
Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.

Возможное перемещение системы – это малое перемещение, при котором не нарушаются связи, наложенные на систему.

Уравнения Лагранжа

Число обобщенных координат n совпадает с числом степеней свободы системы.

Уравнения Лагранжа – это уравнения движения механической системы в обобщенных координатах:

Здесь T – кинетическая энергия. Она является функцией от обобщенных координат, скоростей и, возможно, времени. Поэтому ее частная производная также является функцией от обобщенных координат, скоростей и времени. Далее нужно учесть, что координаты и скорости являются функциями от времени. Поэтому для нахождения полной производной по времени нужно применить правило дифференцирования сложной функции:
.

Использованная литература:
А. П. Маркеев, Теоретическая механика, «Ижевская республиканская типография», 1999.
Н. Н. Никитин, Курс теоретической механики, «Высшая школа», 1990.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.
А. А. Яблонский, Курс теоретической механики, часть 2, динамика «Высшая школа», 1986.

Источник