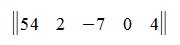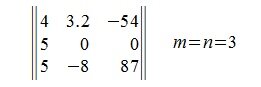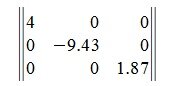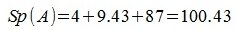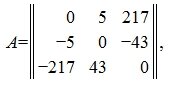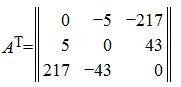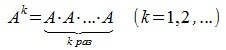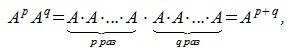Что называют матрицей математика

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

Матрица столбец

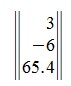
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Нулевая матрица

Квадратная матрица

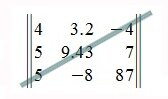
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

Главная диагональ матрицы

Побочная диагональ матрицы

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Единичная матрица

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

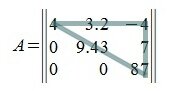
Верхняя треугольная матрица

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Источник

Что такое матрицы, откуда они взялись, и чем они полезны?

Первые упоминания о матрицах или «волшебных квадратах», как их тогда называли, были найдены на территории еще Древнего Китая, однако бум случился намного позже, в середине XVIII века, когда знаменитый математик Габриэль Крамер опубликовал свой труд под названием «Введение в анализ алгебраических кривых», в котором описывался алгоритм решения систем линейных уравнений совершенно новым методом.

Как следствие, в дальнейшем появляются «классический» метод решения Карла Фридриха Гаусса, теорема Гамильтона-Кели, работы Карла Вейерштрасса, Георга Фробениуса и других выдающихся ученых.

Занимательно, что только после всех этих открытий, а именно в 1850 году был непосредственно введен термин матрица, автором которого стал Джеймс Джозеф Сильвестр.

Сегодня термин «матрица» применяется во множестве разных областей: от программирования до кинематографии (здесь должно быть название фильма, о котором вы все подумали).

Матрица в математике – это таблица чисел, состоящая из определенного количества строк (m) и столбцов (n).

Вы встречаетесь с ними каждый день, так как любая числовая информация, занесенная в таблицу, уже в какой-то степени считается матрицей.

Примером могут служить:
● список телефонных номеров;
● различные статистические данные;
● табель успеваемости ученика и многое другое.

Сами матрицы всегда обозначаются прописными латинскими буквами (A, B, C…), а элементы матрицы – строчными (a, b, c…). Индексы обозначают местоположение элемента матрицы в системе, причем первое число – это всегда номер строки, а второе – это всегда номер столбца. Например, а₂₃ находится во второй строке и в третьем столбце, а₃₁ в третьей строке и первом столбце и т.д.

Важно произносить элементы матриц правильно, так а₂₃ будет звучать как «а два три», а не «а двадцать три».

Примеры записи матриц

Для чего нужны матрицы

Теперь выясним, для чего нам так нужны матрицы конкретно в математике?

В качестве примера рассмотрим простейшую систему двух линейных уравнений и решим ее методом сложения, который изучают в школьном курсе.

Оказывается, можно решить эту систему уравнений альтернативным способом, используя матрицы, и называется он метод Крамера.

Вы можете подумать, зачем усложнять решение какими-то матрицами?

В данном случае да, при желании можно эту систему и в уме решить. Но представьте себе систему, состоящую хотя бы из 5 линейных уравнений с пятью неизвестными. А если система состоит из 6, 7 или ещё больше уравнений? Решать её школьным методом, мягко говоря, трудоёмко. Зато применяя тот же метод Крамера, решение будет выглядеть достаточно компактно.

Система с тремя уравнениями

В подтверждение вышесказанного рассмотрим систему уравнений с тремя неизвестными и решим её метод Крамера.

Из этого следует, что матрицы – еще один способ решения систем линейных алгебраических уравнений (СЛАУ).

На основе второго примера убеждаемся в том, что матрицы могут применяться в тех случаях, когда применение школьных методов решения СЛАУ не является рациональным.

На самом деле за прошедшие столетия алгебра матриц изучена более, чем достаточно, и тот факт, что матрицы используются повсеместно однозначно подтверждает необходимость их изучения.

Источник

Математика для чайников. Матрицы и основные действия над ними

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

Операция умножения матриц

И пример с реальными числами. Умножим матрицы:

Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

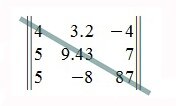
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Источник

Матрица (математика)

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Для матрицы определены следующие алгебраические операции:

Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, можно сопоставить единственную квадратную матрицу порядка n; и обратно — каждой квадратной матрице порядка n может быть сопоставлен единственный линейный оператор, действующий в этом пространстве. [2] Свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.

То же можно сказать о представлении матрицами билинейный (квадратичных) форм.

В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.

Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.

Содержание

История

Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Также волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г. [3]

Определение

Пусть есть два конечных множества и , где и — натуральные числа.

Назовём матрицей размера (читается на ) с элементами из некоторого кольца или поля отображение вида

.

называется элементом матрицы, находящимся на пересечении -той строки и -ого столбца;

Если индекс пробегает множество , а пробегает множество , то совокупность элементов полностью определяет матрицу.

Таким образом, матрица размера состоит в точности из

В соответствии с этим

Сама матрица естественным образом интерпретируется как вектор в пространстве , имеющем размерность . Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.

Если у матрицы количество строк совпадает с количеством столбцов , то такая матрица называется квадратной, а число называется размером квадратной матрицы или её порядком.

Обозначения

Обычно матрицу обозначают заглавной буквой латинского алфавита: пусть

,

тогда — матрица, которая интерпретируется как прямоугольный массив элементов поля вида , где

таким образом, — элемент матрицы , находящийся на пересечении -той строки и -того столбца. В соответствии с этим принято следующее компактное обозначение для матрицы размера :

если нужно просто указать обозначение для элементов матрицы.

Иногда, вместо , пишут , чтобы отделить индексы друг от друга и избежать смешения с произведением двух чисел.

Если необходимо дать развёрнутое представление матрицы в виде таблицы, то используют запись вида

Можно встретить как обозначения с круглыми скобками «(…)», так и обозначения с квадратными скобками «[…]». Реже можно встретить обозначения с двойными прямыми линиями «||…||»).

Поскольку матрица состоит из строк и столбцов, для них используются следующие обозначения:

— это -тая строка матрицы ,

— это -тый столбец матрицы .

Таким образом, матрица обладает двойственным представлением — по строкам:

.

Такое представление позволяет формулировать свойства матриц в терминах строк или в терминах столбцов.

Транспонированная матрица

С каждой матрицей размера связана матрица размера вида

Такая матрица называется транспонированной матрицей для и обозначается так .

Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица размера при этом преобразовании станет матрицей размерностью .

Диагональная матрица

Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных — нулевые , иногда записывается как:

Единичная матрица

Единичная матрица — матрица, при умножении на которую любая матрица (или вектор) остается неизменной, является диагональной матрицей с единичными (всеми) диагональными элементами:

Для ее обозначения чаще всего используется обозначение I или E, а также просто 1 (или 1 специальным шрифтом).

Для обозначения ее элементов также используется символ Кронекера , определяемый как:

при

Нулевая матрица

Для обозначения нулевой матрицы — матрицы, все элементы которой нули (при сложении ее с любой матрицей та остается неизменной, а при умножении на любую получается нулевая матрица) — используется обычно просто 0 или 0 специальным шрифтом, или буква, начертанием похожая на ноль, например .

Вектор-строка и вектор-столбец

Матрицы размера и являются элементами пространств и соответственно:

Операции над матрицами

Умножение матрицы на число

Умножение матрицы на число (обозначение: ) заключается в построении матрицы , элементы которой получены путём умножения каждого элемента матрицы на это число, то есть каждый элемент матрицы равен

Свойства умножения матриц на число:

Сложение матриц

Сложение матриц есть операция нахождения матрицы , все элементы которой равны попарной сумме всех соответствующих элементов матриц и , то есть каждый элемент матрицы равен

Свойства сложения матриц:

Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образуют линейное пространство над полем P (каждая такая матрица является вектором этого пространства). Впрочем, прежде всего во избежание терминологической путаницы, матрицы в обычных контекстах избегают без необходимости (которой нет в наиболее обычных стандартных применениях) и четкого уточнения употребления термина называть векторами.

Умножение матриц

Умножение матриц (обозначение: , реже со знаком умножения ) — есть операция вычисления матрицы , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице должно совпадать с количеством строк в матрице , иными словами, матрица обязана быть согласованной с матрицей . Если матрица имеет размерность , — , то размерность их произведения есть .

Свойства умножения матриц:

Умножение вектора на матрицу

По обычным правилам матричного умножения осуществляется умножение на матрицу слева вектора-столбца, а также умножение вектора-строки на матрицу справа. Поскольку элементы вектора-столбца или вектора-строки можно записать (что обычно и делается), используя один, а не два индекса, это умножение можно записать так:

для вектора-столбца v (получая новый вектор-столбец Av):

для вектора-строки s (получая новый вектор-строку sA):

Вектор-строка, матрица и вектор столбец могут быть умножены друг на друга, давая число (скаляр):

(Порядок важен: вектор-строка слева, вектор-столбец справа от матрицы).

Эти операции являются основой матричного представления линейных операторов и линейных преобразований координат (смены базисов), таких, как повороты, масштабирования, зеркальные отражения, а также (последнее) матричного представления билинейных (квадратичных форм.

Заметим, что обычной мотивировкой введения матриц и определения операции матричного умножения (см.тж.в статье об умножении матриц) является именно введение их, начиная с умножения вектора на матрицу (которое вводится исходя из преобразований базиса или вообще линейных операций над векторами), а уже затем композиции преобразований сопоставляется произведение матриц. Действительно, если новый вектор Av, полученный из исходного вектора v преобразованием, представимым умножением на матрицу A, преобразовать теперь еще раз, преобразованием, представимым умножением на матрицу B, получив B(Av), то, исходя из правила умножения вектора на матрицу, приведенного в начале этого параграфа (используя ассоциативность умножения чисел и меняя порядок суммирования), нетрудно увидеть в результате формулу, дающую элементы матрицы (BA), представляющую композицию первого и второго преобразований, и совпадающую с обычным определением матричного умножения.

Комплексное сопряжение

Если элементами матрицы являются комплексные числа, то комплексно сопряжённая (не путать с эрмитово сопряжённой! см. далее) матрица равна . Здесь — число, комплексно сопряжённое к .

Транспонирование и эрмитово сопряжение

Транспонирование уже обсуждалось выше: если , то . Для комплексных матриц более употребительно эрмитово сопряжение: . С точки зрения операторного взгляда на матрицы, транспонированная и эрмитово сопряжённая матрица — это матрицы оператора, сопряжённого относительно скалярного или эрмитова произведения, соответственно.

Для квадратной матрицы определен след:

(иногда также обозначается как Sp или Spur).

Является инвариантом ортогональных (унитарных) преобразований матрицы, соответствующих преобразованию матричного представления линейного оператора или билинейной (квадратичной) формы при соотвестствующем преобразовании векторного пространства (например, вращении).

Источник