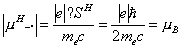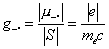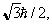Что называют магнитным моментом контура

Магнитный момент

Полезное

Смотреть что такое «Магнитный момент» в других словарях:

Магнитный момент — Размерность L2I Единицы измерения СИ А⋅м2 … Википедия

МАГНИТНЫЙ МОМЕНТ — основная величина, характеризующая магн. свойства в ва. Источником магнетизма (М. м.), согласно классич. теории эл. магн. явлений, явл. макро и микро(атомные) электрич. токи. Элем. источником магнетизма считают замкнутый ток. Из опыта и классич.… … Физическая энциклопедия

МАГНИТНЫЙ МОМЕНТ — векторная величина, характеризующая вещество как источник магнитного поля. Макроскопический магнитный момент создают замкнутые электрические токи и упорядоченно ориентированные магнитные моменты атомных частиц. У микрочастиц различают орбитальные … Большой Энциклопедический словарь

МАГНИТНЫЙ МОМЕНТ — МАГНИТНЫЙ МОМЕНТ, измерение силы постоянного магнита или токонесущей катушки. Это максимальная поворотная сила (поворотный момент), приложенная к магниту, катушке или электрическому заряду в МАГНИТНОМ ПОЛЕ, деленная на силу поля. Заряженные… … Научно-технический энциклопедический словарь

МАГНИТНЫЙ МОМЕНТ — физ. величина, характеризующая магнитные свойства тел и частиц вещества (электронов, нуклонов, атомов и т.д.); чем больше магнитный момент, тем сильнее (см.) тела; магнитным моментом определяются магнитное (см.). Поскольку всякий электрический… … Большая политехническая энциклопедия

МАГНИТНЫЙ МОМЕНТ — (Magnetic moment) произведение из магнитной массы данного магнита на расстояние между его полюсами. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь

магнитный момент — Хар ка магн. св в тела, усл. выраж. произвед. величины магн. заряда в каждом полюсе на расстояние м ду полюсами. [http://metaltrade.ru/abc/a.htm] Тематики металлургия в целом EN magnetic moment … Справочник технического переводчика

магнитный момент — векторная величина, характеризующая вещество как источник магнитного поля. Макроскопический магнитный момент создают замкнутые электрические токи и упорядоченно ориентированные магнитные моменты атомных частиц. У микрочастиц различают орбитальные … Энциклопедический словарь

МАГНИТНЫЙ МОМЕНТ — – основная величина, характеризующая магнитные свойства вещества. Элементарным источником магнетизма считается электрический ток. Вектор, определяющийся произведением силы тока на площадь контура замкнутого тока, есть магнитный момент. По… … Палеомагнитология, петромагнитология и геология. Словарь-справочник.

магнитный момент — elektromagnetinis momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis dydis, kurio vektorinė sandauga su vienalyčio magnetinio srauto tankiu yra lygi sukimo momentui: m · B = T; čia m – magnetinio momento vektorius, B… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

Учебники

Журнал «Квант»

Общие

Магнитная индукция

Для количественного описания магнитного поля можно воспользоваться контуром с током. Так как контур с током испытывает ориентирующее действие поля, то на него в магнитном поле действует пара сил, которая создает момент сил относительно некоторой неподвижной оси. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств контура. Для плоского контура с током I величина, равная произведению силы тока I на площадь S, ограниченную контуром, называется магнитным моментом контура p_m.

Магнитный момент — векторная величина. Его направление совпадает с направлением положительной нормали к контуру.

\vec n\) — единичный вектор нормали к плоскости контура.

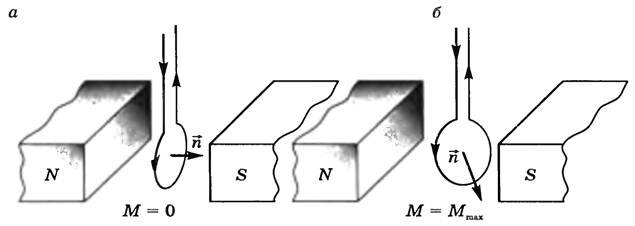
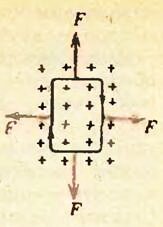
Опыт показывает, что вращающий момент зависит от расположения контура в магнитном поле. Вращающий момент равен О, если магнитное поле перпендикулярно плоскости контура (рис. 2, а), и максимален, если нормаль к контуру перпендикулярна магнитному полю (рис. 2, б).

Максимальный вращающий момент, как показывает опыт, пропорционален силе тока I и площади контура рамки с током, т.е.

Если в данную точку магнитного поля помещать контуры с разными магнитными моментами, то на них будут действовать различные вращающие моменты, однако отношение \(

\frac>\) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией.

Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой магнитного поля, численно равная максимальному вращающему моменту, действующему на контур с единичным магнитным моментом, и направленная вдоль положительной нормали к контуру.

Модуль магнитной индукции равен

Единицей магнитной индукции в СИ является тесла (Тл).

1 Тл — магнитная индукция такого однородного поля, в котором на контур с магнитным моментом 1 А·м 2 действует вращающий момент 1 Н·м.

\vec B\) полностью характеризует магнитное поле. В каждой точке может быть найден ее модуль и направление.

Поле, в каждой точке которого модуль и направление магнитной индукции одинаковы (\(

Если магнитное поле образовано системой n проводников с токами, то, имеет место принцип суперпозиции магнитных полей: магнитная индукция поля системы токов равна геометрической сумме магнитных индукцией полей каждого из токов в отдельности:

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 316-317.

Источник

Учебники

Журнал «Квант»

Общие

Кикоин А.К. Магнитный момент тока //Квант. — 1986. — № 3. — С. 22-23.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Из курса физики девятого класса («Физика 9», § 88) известно, что на прямолинейный проводник длиной l с током I, если он помещен в однородное магнитное поле с индукцией \(

\vec B\), действует сила \(

\vec F\), равная по модулю

где α — угол между направлением тока и вектором магнитной индукции. Направлена эта сила перпендикулярно и полю, и току (по правилу левой руки).

Прямолинейный проводник — это только часть электрической цепи, поскольку электрический ток всегда замкнут. А как магнитное поле действует на замкнутый ток, точнее — на замкнутый контур с током?

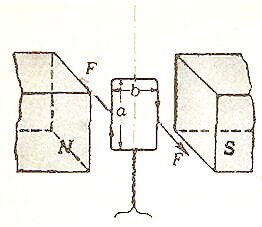
На рисунке 1 в качестве примера показан контур в форме прямоугольной рамки со сторонами a и b, по которой в указанном стрелками направлении течет ток I.

Рамка помещена в однородное магнитное поле с индукцией \(

\vec B\) так, что в начальный момент вектор \(

\vec B\) лежит в плоскости рамки и параллелен двум ее сторонам. Рассматривая каждую из сторон рамки по отдельности, мы найдем, что на боковые стороны (длиной а) действуют силы, равные по модулю F = BIa и направленные в противоположные стороны. На две другие стороны силы не действуют (для них sin α = 0). Каждая из сил F относительно оси, проходящей через середины верхней и нижней сторон рамки, создает момент силы (вращающий момент), равный \(

\frac<2>\) — плечо силы). Знаки моментов одинаковы (обе силы поворачивают рамку в одну сторону), так что общий вращающий момент М равен BIab, или, поскольку произведение ab равно площади S рамки,

Под действием этого момента рамка начнет поворачиваться (если смотреть сверху, то по часовой стрелке) и будет поворачиваться до тех пор, пока не станет своей плоскостью перпендикулярно вектору индукции \(

В этом положении сумма сил и сумма моментов сил равны нулю, и рамка находится в состоянии устойчивого равновесия. (На самом деле рамка остановится не сразу — в течение некоторого времени она будет совершать колебания около своего положения равновесия.)

Нетрудно показать (сделайте это самостоятельно), что в любом промежуточном положении, когда нормаль к плоскости контура составляет произвольный угол β с индукцией магнитного поля, вращающий момент равен

Теперь мы можем сказать, что контур с током в однородном магнитном поле устанавливается так, чтобы его магнитный момент «смотрел» в сторону того поля, которое вызвало его поворот.

Известно, что не только контуры с током обладают свойством создавать собственное магнитное поле и поворачиваться во внешнем поле. Такие же свойства наблюдаются и у намагниченного стержня, например у стрелки компаса.

Еще в 1820 году замечательный французский физик Ампер высказал идею о том, что сходство поведения магнита и контура с током объясняется тем, что в частицах магнита существуют замкнутые токи. Теперь известно, что в атомах и молекулах действительно есть мельчайшие электрические токи, связанные с движением электронов по своим орбитам вокруг ядер. Из-за этого атомы и молекулы многих веществ, например парамагнетиков, обладают магнитными моментами. Поворот этих моментов во внешнем магнитном поле и приводит к намагничиванию парамагнитных веществ.

Выяснилось и другое. Все частицы, входящие в состав атома, обладают также магнитными моментами, вовсе не связанными с какими-либо движениями зарядов, то есть с токами. Для них магнитный момент является таким же «врожденным» качеством, как заряд, масса и т. п. Магнитным моментом обладает даже частица, не имеющая электрического заряда,— нейтрон, составная часть атомных ядер. Магнитным моментом обладают поэтому и атомные ядра.

Таким образом, магнитный момент — одно из самых важных понятий в физике.

Источник

Что называют магнитным моментом контура

Пусть в однородное магнитное поле помещена рамка с током (рис. 4.13). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором и нормалью к площади :

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

Это выражение также можно использовать для определения индукции магнитного поля:

Величину, равную произведению , называют магнитным моментом контура Р_т. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

Источник

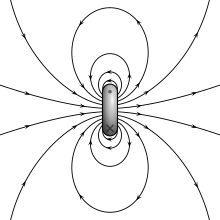
Магнитное поле магнитного диполя пропорционально его магнитному дипольному моменту. Дипольная составляющая магнитного поля объекта симметрична относительно направления его магнитного дипольного момента и уменьшается как куб, обратный расстоянию от объекта.

СОДЕРЖАНИЕ

Определение, единицы и измерение

Определение

Магнитный момент можно определить как вектор, связывающий выравнивающий момент на объекте от внешнего магнитного поля с самим вектором поля. Отношения задаются:

Это определение основано на том, как в принципе можно измерить магнитный момент неизвестного образца. Для токовой петли это определение приводит к тому, что величина магнитного дипольного момента равна произведению тока на площадь петли. Кроме того, это определение позволяет рассчитать ожидаемый магнитный момент для любого известного макроскопического распределения тока.

Альтернативное определение полезно для термодинамических расчетов магнитного момента. В этом определении магнитный дипольный момент системы представляет собой отрицательный градиент ее внутренней энергии U _{int по} отношению к внешнему магнитному полю:

Как правило, внутренняя энергия включает в себя энергию собственного поля системы плюс энергию внутренней работы системы. Например, для атома водорода в состоянии 2p во внешнем поле энергия собственного поля пренебрежимо мала, поэтому внутренняя энергия по существу является собственной энергией состояния 2p, которая включает кулоновскую потенциальную энергию и кинетическую энергию электрона. Энергия поля взаимодействия между внутренними диполями и внешними полями не является частью этой внутренней энергии.

Единицы

Измерение

Отношение к намагничиванию

Модели

Модель магнитного полюса

Модель петли амперова

После того, как Ганс Кристиан Эрстед обнаружил, что электрические токи создают магнитное поле, а Андре-Мари Ампер обнаружил, что электрические токи притягивают и отталкивают друг друга, как магниты, было естественным предположить, что все магнитные поля возникают из-за контуров электрического тока. В этой модели, разработанной Ампером, элементарный магнитный диполь, из которого состоят все магниты, представляет собой достаточно малую амперовую петлю тока I. Дипольный момент этой петли равен

Локализованные текущие распределения

таким образом определяется магнитный дипольный момент для амперовской петли.

Магнитный момент соленоида

Квантовая механическая модель

Воздействие внешнего магнитного поля

Крутящий момент

Крутящий момент τ на объекте, имеющем магнитный дипольный момент m в однородном магнитном поле B, равен:

Это справедливо на данный момент из-за любого локализованного распределения тока при условии, что магнитное поле однородно. Для неоднородного B уравнение также справедливо для крутящего момента относительно центра магнитного диполя при условии, что магнитный диполь достаточно мал.

Сила на мгновение

Магнитный момент во внешнем магнитном поле имеет потенциальную энергию U :

В случае использования пары монополей (т.е. модели электрического диполя) сила равна

И одно можно выразить через отношение

Магнетизм

Воздействие на окружающую среду

Магнитное поле магнитного момента

Магнитное поле магнитного диполя зависит от силы и направления магнитного момента магнита, но уменьшается в виде куба расстояния, так что: м <\ displaystyle \ mathbf >

Силы между двумя магнитными диполями

Как обсуждалось ранее, сила, прилагаемая дипольной петлей с моментом m ₁ к другой с моментом m _2, равна

Сила, действующая на m _1, находится в противоположном направлении.

Крутящий момент одного магнитного диполя на другом

Крутящий момент магнита 1 на магните 2 равен

Теория, лежащая в основе магнитных диполей

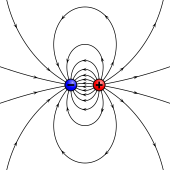
Магнитное поле любого магнита можно смоделировать с помощью ряда членов, для которых каждый член более сложен (имеет более мелкие угловые детали), чем предыдущий. Первые три члена этой серии называются монополем (представлен изолированным северным или южным магнитным полюсом), диполем (представлен двумя равными и противоположными магнитными полюсами) и квадруполем (представлен четырьмя полюсами, которые вместе образуют два равных и противоположных полюса). диполи). Величина магнитного поля для каждого члена уменьшается с расстоянием прогрессивно быстрее, чем предыдущий член, так что на достаточно больших расстояниях первый ненулевой член будет доминировать.

Магнитные потенциалы

Традиционно уравнения для магнитного дипольного момента (и члены более высокого порядка) выводятся из теоретических величин, называемых магнитными потенциалами, с которыми проще иметь дело с математической точки зрения, чем с магнитными полями.

Оба этих потенциала могут быть рассчитаны для любого произвольного распределения тока (для модели амперной петли) или распределения магнитного заряда (для модели магнитного заряда) при условии, что они ограничены достаточно малой областью, чтобы дать:

С точки зрения магнитного полюса, первый ненулевой член скалярного потенциала равен

Его можно представить в терминах плотности напряженности магнитного полюса, но более полезно выразить в терминах поля намагничивания как: м <\ displaystyle \ mathbf >

В обоих уравнениях используется один и тот же символ, поскольку они дают эквивалентные результаты вне магнита. м <\ displaystyle \ mathbf >

Внешнее магнитное поле, создаваемое магнитным дипольным моментом

Следовательно, плотность магнитного потока для магнитного диполя в модели амперной петли равна

Кроме того, напряженность магнитного поля равна ЧАС <\ displaystyle \ mathbf >

Внутреннее магнитное поле диполя

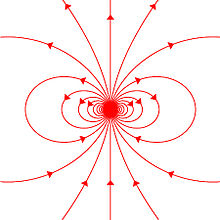
Две модели диполя (токовая петля и магнитные полюса) дают одинаковые предсказания для магнитного поля вдали от источника. Однако внутри области источника они дают разные прогнозы. Магнитное поле между полюсами (см. Определение магнитного полюса на рисунке ) находится в направлении, противоположном магнитному моменту (который указывает от отрицательного заряда к положительному), в то время как внутри токовой петли оно находится в том же направлении (см. Рисунок Направо). Пределы этих полей также должны быть разными, поскольку источники сжимаются до нулевого размера. Это различие имеет значение только в том случае, если дипольный предел используется для расчета полей внутри магнитного материала.

Если магнитный диполь создается путем уменьшения и уменьшения токовой петли, но при сохранении постоянного произведения тока и площади, ограничивающее поле равно

В отличие от выражений в предыдущем разделе, этот предел верен для внутреннего поля диполя.

Если магнитный диполь сформирован путем взятия «северного полюса» и «южного полюса», приведения их все ближе и ближе друг к другу, но при сохранении постоянного произведения заряда магнитного полюса и расстояния, ограничивающее поле равно

Связь с угловым моментом

Это похоже на магнитный момент, создаваемый очень большим количеством заряженных частиц, составляющих этот ток:

Сравнение двух уравнений приводит к:

Несмотря на то, что атомные частицы нельзя точно описать как орбитальные (и вращающиеся) зарядовые распределения с однородным отношением заряда к массе, эту общую тенденцию можно наблюдать в атомном мире, так что:

где g- фактор зависит от частицы и конфигурации. Например, g- фактор для магнитного момента электрона, вращающегося вокруг ядра, равен единице, в то время как g- фактор для магнитного момента электрона, обусловленного его собственным угловым моментом ( спином ), немного больше 2. g- фактор атомов и молекул должны учитывать орбитальный и собственный моменты его электронов, а также, возможно, собственный момент его ядер.

Атомы, молекулы и элементарные частицы

Точно так же магнитный момент стержневого магнита представляет собой сумму вносящих вклад магнитных моментов, которые включают собственный и орбитальный магнитные моменты неспаренных электронов материала магнита и ядерные магнитные моменты.

Магнитный момент атома

Для атома отдельные электронные спины складываются, чтобы получить общий спин, и отдельные орбитальные угловые моменты складываются, чтобы получить общий орбитальный угловой момент. Затем эти два суммируются с использованием связи по угловому моменту, чтобы получить общий угловой момент. Для атома без ядерного магнитного момента величина дипольного момента атома тогда равна м атом <\ displaystyle <\ mathfrak > _ <\ text >>

м атом знак равно грамм J μ B j ( j + 1 ) <\ displaystyle <\ mathfrak > _ <\ text > = g _ <\ rm > \, \ mu _ <\ rm > \, <\ sqrt >>

Отрицательный знак возникает из-за того, что электроны имеют отрицательный заряд.

Целое число м (не следует путать с моментом, ) называется магнитным квантовым числом или экваториальное квантовое число, которое может принимать любой из 2 J + 1 значений: м <\ displaystyle <\ mathfrak >>

Из-за углового момента динамика магнитного диполя в магнитном поле отличается от динамики электрического диполя в электрическом поле. Поле действительно оказывает крутящий момент на магнитный диполь, стремясь выровнять его с полем. Однако крутящий момент пропорционален скорости изменения углового момента, поэтому происходит прецессия : изменяется направление вращения. Такое поведение описывается уравнением Ландау – Лифшица – Гильберта :

Магнитный момент электрона

Магнитный момент электрона равен

Магнитный момент ядра

Магнитный момент молекулы

Примеры молекулярного магнетизма

Элементарные частицы

Источник