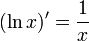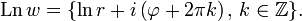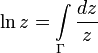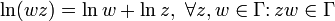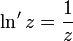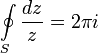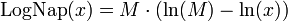Логарифм (понятие).

Говоря другими словами логарифм числа b по основанию а формулируется как показатель степени, в которую надо возвести число a, чтобы получить число b (логарифм существует только у положительных чисел).

Из данной формулировки вытекает, что вычисление x= log_α b, равнозначно решению уравнения a x =b.

Достаточно часто используются вещественные логарифмы с основаниями 2 (двоичный), е число Эйлера e ≈ 2,718 (натуральный логарифм) и 10 (десятичный).

На данном этапе целесообразно рассмотреть образцы логарифмов log₇2, ln√5, lg0.0001.

А записи lg(-3), log_-33.2, log_-1-4.3 не имеют смысла, так как в первой из них под знаком логарифма помещено отрицательное число, во второй – отрицательное число в основании, а в третьей – и отрицательное число под знаком логарифма и единица в основании.

Условия определения логарифма.

Возьмем условие a≠1. Поскольку единица в любой степени равна единице, то равенство x=log_α b может существовать лишь при b=1, но при этом log₁ 1 будет любым действительным числом. Для исключения этой неоднозначности и берется a≠1.

Докажем необходимость условия a>0. При a=0 по формулировке логарифма может существовать только при b=0. И соответственно тогда log₀0 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0. А при a 0.

И последнее условие b>0 вытекает из неравенства a>0, поскольку x=log_α b, а значение степени с положительным основанием a всегда положительно.

Особенности логарифмов.

Логарифмы характеризуются отличительными особенностями, которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов. При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.

Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.

Источник

Логарифмы

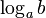
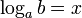
Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: . Из определения следует, что записи и a x = b равносильны.

Содержание

Вещественный логарифм

Логарифм вещественного числа log_ab имеет смысл при .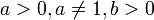

Наиболее широкое применение нашли следующие виды логарифмов.

Свойства

Натуральные логарифмы

Для производной натурального логарифма справедлива простая формула:

По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т. п.

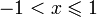
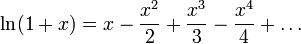При справедливо равенство

(1)

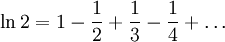Формула (1) не имеет большой практической ценности из-за того, что ряд очень медленно сходится и значение x ограничено весьма узким диапазоном. Однако нетрудно получить из неё более удобную формулу:

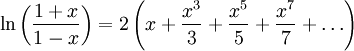(2)

Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.

Связь с десятичным логарифмом: .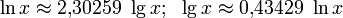

Десятичные логарифмы

Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:

Логарифмическая шкала также широко применяется для выявления показателя степени в степенных зависимостях и коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой, более простой для исследования.

Комплексный логарифм

Многозначная функция

,

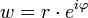
то логарифм 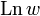находится по формуле:

Из формулы следует:

Примеры (приведено главное значение логарифма):

Аналогично рассматриваются комплексные логарифмы с другим основанием. Следует, однако, быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:

iπ = ln( − 1) = ln(( − i) 2 ) = 2ln( − i) = 2( − iπ / 2) = − iπ — явная нелепость.

Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви ( k = − 1 ). Причина ошибки — неосторожное использования свойства 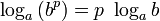, которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.

Аналитическое продолжение

При этом, если Γ — простая кривая (без самопересечений), то для чисел, лежащих на ней, логарифмические тождества можно применять без опасений, например

Из формулы аналитического продолжения следует, что на любой ветви логарифма

Интеграл берётся в положительном направлении (против часовой стрелки). Это тождество лежит в основе теории вычетов.

Риманова поверхность

Исторический очерк

Вещественный логарифм

Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.

В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером, утвердился в науке.

Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:

Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.

Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.

Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).

К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.

Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.

Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.

Комплексный логарифм

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Даламбером и Эйлером. Бернулли и Даламбер считали, что следует определить log(-x) = log(x). Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.

Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.

Логарифмические таблицы

Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются. Лаплас говорил, что изобретение логарифмов «продлило жизнь астрономов», многократно ускорив процесс вычислений.

Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега (1783) появилось только в 1857 году в Берлине (таблицы Бремивера).

В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов.

Таблицы Брадиса (1921) использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.

Профессиональный сборник для точных вычислений.

Источник

Логарифм. Основное логарифмическое тождество.

Основное логарифмическое тождество и логарифм тесно взаимосвязаны. И по сути, основное логарифмическое тождество является математической записью определения логарифма. Разберем подробно, что такое логарифм, откуда он произошел.

Когда, к примеру, в уравнении a x = b число а положительно, а число b отрицательно, то у такого уравнения корней нет. Но если только а и b положительны и а ≠ 1, то оно непременно имеет исключительно один единственный корень. Достаточно известный факт, что график показательной функции у = а х непременно пересекается с прямой у = b и притом исключительно в одной точке. Абсцисса точки пересечения и будут корнем уравнения.

Для обозначения корня уравнения a x = b принято употреблять log_ab (произносим: логарифм числа b по основанию а).

Логарифм числа b по основанию а это показатель степени, в которую нужно возвести число а, чтобы получить число b причем a > 0, a ≠ 1, b > 0.

Исходя из определения, получаем основное логарифмическое тождество:

Следствием основного логарифмического тождества является нижеследующее правило.

Из равенства двух вещественных логарифмов получаем равенство логарифмируемых выражений.

Действительно, когда log_ab = log_aс, то , откуда, b = c.

Рассмотрим, почему для логарифмического тождества взяты ограничения a > 0, a ≠ 1, b > 0.

Первое условие a ≠ 1.

Общеизвестно, что единица в любой степени будет единица, и равенство x = log_ab может существовать лишь при b = 1, но при этом log₁1 будет любым действительным числом. Для недопущения этой неоднозначности и принимается a ≠ 1.

Обоснуем необходимость условия a > 0.

При a = 0 по определению логарифма может существовать только при b = 0. И следовательно тогда log₀0 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Не допустить эту неоднозначность дает условие a ≠ 0. А при a 0.

И заключительное условие b > 0 является следствием из неравенства a > 0, так как x = log_ab, а значение степени с положительным основанием a всегда положительно.

Источник

Свойства логарифмов

Определение логарифма

Основное логарифмическое тождество

Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a &#x2260 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.

Два очевидных следствия определения логарифма

Логарифм произведения и логарифм частного

log a ( b c ) = log a b + log a c ( a > 0, a ≠ 1, b > 0, c > 0 ) (5)

log a b c = log a b − log a c ( a > 0, a ≠ 1, b > 0, c > 0 ) (6)

Действительно, выражение log a ( f ( x ) g ( x ) ) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Степень можно выносить за знак логарифма

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a ( f ( x ) 2 = 2 log a f ( x )

Формула перехода к новому основанию

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

log a b = 1 log b a ( a > 0, a ≠ 1, b > 0, b ≠ 1 ) (9)

Десятичные и натуральные логарифмы

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок № 24. Логарифм. Свойства логарифмов.

Перечень вопросов, рассматриваемых в теме

1. Определение логарифма.

2. Основное логарифмическое тождество.

3. Свойства логарифмов.

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Логарифмирование – это действие нахождения логарифма числа.

Основное логарифмическое тождество:

Свойства логарифмов. При , справедливы равенства:

— логарифм произведения: ;

— логарифм частного: ;

— логарифм степени: .

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение имеет корень 5, т. к. значит , В уравнении число 5 не является степенью 2, значит предыдущий способ решения не подходит. Нам известно, что уравнение имеет единственный корень. Посмотрим это на графике.

Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.

Дадим определение логарифма.

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Т. е. логарифм числа по основанию , есть некоторое число такое, что .

, т. к. выполнены все условия определения:

1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) .

, т. к. выполнены все условия определения:

1) ; 2) 2 > 0, 2 ≠ 1; 3) .

Это действие называется логарифмированием.

Логарифмирование – это действие нахождения логарифма числа.

Существует краткая запись определения логарифма:

так называемое основное логарифмическое тождество. Его используют при вычислениях.

(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)

(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)

Решим несколько задач с использованием определения логарифма.

Задача 1. Вычислить .

Задача 2. Вычислить .

Решение. Для вычисления воспользуемся свойствами степеней: 1) , 2) и основным логарифмическим тождеством: .

.

Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.

1. Логарифм произведения.

Логарифм произведения чисел по основанию равен сумме логарифма по основанию и логарифма по основанию .

2. Логарифм частного.

Логарифм частного чисел по основанию равен разности логарифма по основанию и логарифма по основанию .

3. Логарифм степени.

Логарифм числа по основанию равен произведению показателя и логарифма по основанию .

Важно! Свойства выполняются при ,

Примеры и разбор решения заданий тренировочного модуля

№ 1. Вычислите: .

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

Представим в виде степени с рациональным показателем: . Далее воспользуемся свойством нахождения логарифма степени: . Вспоминаем таблицу квадратов: , значит , . Ответ: .

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

.

Источник