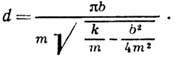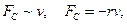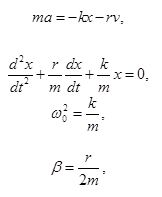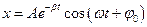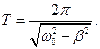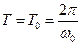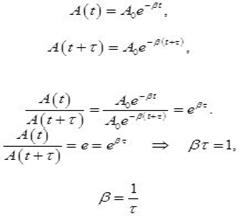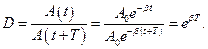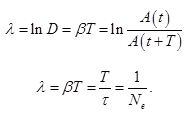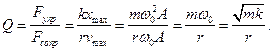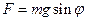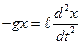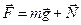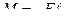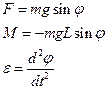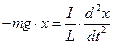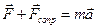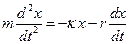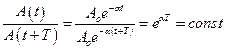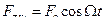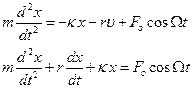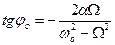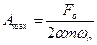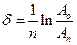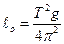Что называют логарифмическим декрементом затухания

Что называют логарифмическим декрементом затухания

§6 Затухающие колебания

Декремент затухания. Логарифмический декремент затухания.

Добротность

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона

— дифференциальное уравнение затухающих колебаний.

— у равнение затухающих колебаний.

ω – частота затухающих колебаний:

Период затухающих колебаний:

Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово­рить, когда β мало.

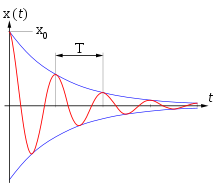
Если затухания выражены слабо (β→0), то . Затухающие колебания можно

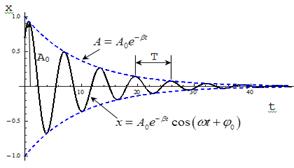
рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз

Логарифмический декремент затухания равен логарифму D :

Еще одной характеристикой колебательной система является добротность Q .

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.

Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

§7 Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

(1)

— дифференциальное уравнение вынуж­денных колебаний.

Это дифференциальное уравнение является линейным неоднородным.

Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:

Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:

(2)

Частное решение этого уравнения будем искать в виде:

Это комплексное число удобно представить в виде

Его вещественная часть, являвшаяся решением уравнения (1) равна:

(3)

(4)

Слагаемое Х_о.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механи­ческой системы, называется резонансом.

Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ω_рез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).

Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то

При ω→0 все кривые приходят к значению — статическое отклонение.

Источник

ДЕКРЕМЕНТ ЗАТУХАНИЯ

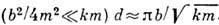
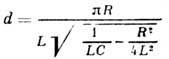
При малом затухании . Аналогично для электрич. контура, состоящего из индуктивности L, активного сопротивления R и ёмкости С, Д. з.

.

При малом затухании .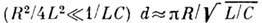

Для нелинейных систем закон затухания колебаний отличен от закона 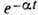, т. е. отношение двух последующих «амплитуд» (и логарифм этого отношения) не остаётся постоянным; поэтому Д. з. не имеет такого определ. смысла, как для систем линейных.

Полезное

Смотреть что такое «ДЕКРЕМЕНТ ЗАТУХАНИЯ» в других словарях:

ДЕКРЕМЕНТ ЗАТУХАНИЯ — (от лат. decrementum уменьшение) характеристика быстроты затухания колебаний: d = ln(A1/A2), где А1 и А2 амплитуды двух колебаний, следующих друг за другом в одну и ту же сторону … Большой Энциклопедический словарь

ДЕКРЕМЕНТ ЗАТУХАНИЯ — (Decrement) величина, характеризующая постепенное затухание колебаний. Д. равен отношению двух амплитуд, следующих одна за другой через один период. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза… … Морской словарь

декремент затухания — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN damping decrement … Справочник технического переводчика

декремент затухания — (от лат. decrementum уменьшение), количественная характеристика быстроты затухания колебаний в линейной системе: Δ = ln(А1/А2), где А1 и А2 два последующих максимальных отклонения колеблющейся величины в одну и ту же сторону. * * * ДЕКРЕМЕНТ… … Энциклопедический словарь

декремент затухания — slopimo dekrementas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiantis virpesių amplitudės sumažėjimą per vieną periodą. atitikmenys: angl. damping ratio vok. Dämpfungsverhältnis, n rus. декремент затухания, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

декремент затухания — slopinimo dekrementas statusas T sritis automatika atitikmenys: angl. damping decrement; damping ratio vok. Dämpfungsbeiwert, m; Dämpfungsdekrement, n; Dämpfungsgrad, m; Dämpfungsverhältnis, n rus. декремент затухания, m; относительное затухание … Automatikos terminų žodynas

декремент затухания — slopimo dekrementas statusas T sritis automatika atitikmenys: angl. attenuation decrement; attenuation ratio vok. Dämpfungsgrad, m; Dämpfungsmaß, n rus. декремент затухания, m pranc. décrément d affaiblissement, m … Automatikos terminų žodynas

декремент затухания — slopinimo dekrementas statusas T sritis fizika atitikmenys: angl. damping decrement vok. Dämpfungsdekrement, n rus. декремент затухания, m pranc. décrément d’amortissement, m … Fizikos terminų žodynas

декремент затухания — rus коэффициент (м) звукопоглощения, коэффициент (м) затухания (звука); коэффициент (м) демпфирования; декремент (м) затухания eng damping coefficient, damping factor fra coefficient (m) d amortissement (m) deu Dämpfungsfaktor (m),… … Безопасность и гигиена труда. Перевод на английский, французский, немецкий, испанский языки

Декремент затухания — количественная характеристика быстроты затухания колебаний. Д. з. δ равен натуральному логарифму отношения двух последующих максимальных отклонений х колеблющейся величины в одну и ту же сторону: Д. з. величина, обратная… … Большая советская энциклопедия

Источник

Логарифмический декремент колебаний

Логарифмический декремент колебаний — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины в одну и ту же сторону:

Логарифмический декремент колебаний равен декременту, умноженному на период колебаний:

Полезное

Смотреть что такое «Логарифмический декремент колебаний» в других словарях:

логарифмический декремент колебаний — логарифмический декремент Ндп. логарифмический декремент затухания Натуральный логарифм отношения двух последовательных максимальных или минимальных значений величины при затухающих свободных колебаниях. Пояснения 1)Некоторые величины и… … Справочник технического переводчика

Логарифмический декремент колебаний — 107. Логарифмический декремент колебаний Логарифмический декремент Ндп. Логарифмический декремент затухания Натуральный логарифм отношения двух последовательных максимальных или минимальных значений величины при затухающих свободных колебаниях… … Словарь-справочник терминов нормативно-технической документации

Логарифмический декремент затухания — D Величина, показывающая скорость затухания собственных колебаний и определяемая как натуральный логарифм отношения следующих друг за другом амплитуд колебаний Источник … Словарь-справочник терминов нормативно-технической документации

логарифмический декремент — logarithmic decrement Натуральный логарифм отношения двух любых последовательных одинакового знака максимальных амплитуд при затухании одночастотных колебаний. Шифр IFToMM: 3.9.38 Раздел: КОЛЕБАНИЯ В МЕХАНИЗМАХ … Теория механизмов и машин

ДЕКРЕМЕНТ ЗАТУХАНИЯ — (от лат. decrementum уменьшение, убыль), количественная хар ка быстроты затухания колебаний. Д. з. d равен натуральному логарифму отношения двух последующих макс. отклонений х колеблющейся величины в одну и ту же сторону: d=ln(x1/x2). Д. з.… … Физическая энциклопедия

ДЕКРЕМЕНТ ЗАТУХАНИЯ — логарифмический (от лат. decrementum уменьшениеубыль) количеств. хар ка затухания колебаний в линейной системе. Д. з. равен натур. логарифму отношения двух последовательных Макс. отклонений колеблющейся величины в одну и ту же сторону … Большой энциклопедический политехнический словарь

Затухание колебаний — характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто носит колебательный характер … Энциклопедия техники

затухание колебаний — затухание колебаний — характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто… … Энциклопедия «Авиация»

затухание колебаний — затухание колебаний — характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто… … Энциклопедия «Авиация»

Затухание колебаний — уменьшение интенсивности колебаний с течением времени, обусловленное потерей энергии колебательной системой. Простейшим случаем убыли энергии колебания является превращение её в тепло вследствие трения в механических системах и… … Большая советская энциклопедия

Источник

Затухающие колебания. Логарифмический декремент затухания. Добротность.

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения:

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r. По второму закону Ньютона

— дифференциальное уравнение затухающих колебаний.

— уравнение затухающих колебаний.

ω – частота затухающих колебаний: Период затухающих колебаний: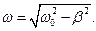

Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово­рить, когда β мало. Если затухания выражены слабо (β→0), то

Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D, который равен отношению амплитуд, отстоящих по времени на период:

Логарифмический декремент затухания равен логарифму D:

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ. Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии. Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

Источник

Определение логарифмического декремента

Затухания и приведенной длины физического маятника

Литература

1. Детлаф А.А., Яворский Б.М. Курс физики. ‑ М., 1989. С. 298 – 314.

2. Методические указания к выполнению лабораторных работ по физике. Раздел «Механика материальной точки». / МТИПП. ‑ М., 1990. С 18 – 31.

Введение

Всякое движение, в котором наблюдается повторяемость во времени значений физических величин, определяющих это движение, называется колебательным движением.

Гармоническим колебательным движением называется такое движение, при котором величина, характеризующая состояние системы, изменяется со временем по закону синуса или косинуса, т.е. уравнение гармонических колебаний имеет вид:

, (1)

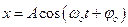
где x – смещение от положения равновесия;

A – амплитуда колебаний – наибольшее смещение от положения равновесия;

– фаза колебаний;

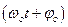
j_о – начальная фаза колебаний;

w_о – собственная циклическая частота колебаний – это число колебаний за 2p секунд.

Время одного полного колебания Т называется периодом колебаний. Количество колебаний в единицу времени называется частотой колебаний 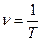. Между периодом, частотой и циклической частотой существует связь:

(2)

Если выражение (1) продифференцировать по времени, то получим закон изменения скорости от времени

(3)

Продифференцировав (3) еще раз по времени, найдем закон зависимости ускорения от времени:

(4)

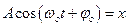
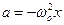
учитывая, что , получим

(5)

Последнее уравнение показывает, что при гармонических колебаниях ускорение пропорционально величине смещения и всегда направлено противоположно смещению.

Примерами систем, в которых могут возникать гармонические колебания, могут служить мятники: пружинный, математический и физический.

Рассмотрим пружинный маятник – грузик на идеально упругой пружине при отсутствии трения. На примере его движения получим дифференциальное уравнение гармонических колебаний.

Чтобы система (маятник) совершала гармонические колебания, необходимо воздействие на нее упругой или квазиупругой силы, изменяющейся при смещении системы от положения равновесия по закону:

(6)

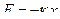
Эта сила, пропорциональна смещению и всегда направлена к положению равновесия. Применим второй закон Ньютона к пружинному маятнику.

Возвращающая сила 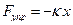, действуя на тело массой m, создает ускорение а. Согласно второму закону Ньютона

Колебания происходят вдоль оси х (рис.1), поэтому спроецируем векторное уравнение на ось ОХ :

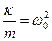
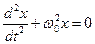
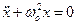
Поделив все члены на m, перенеся их в одну часть равенства, обозначив , получим окончательный вид дифференциального уравнения гармонических колебаний пружинного маятника:

или , (7)

где – собственная частота колебаний пружинного маятника;

– период колебаний (8)

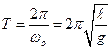
Решением уравнения (7) является уравнение (1).

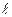
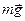
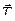
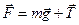
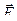
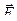
Рассмотрим математический маятник – это материальная точка, подвешенная на невесомой и нерастяжимой нити длиною (рис. 2). На грузик m действуют сила тяжести и сила натяжения нити . Равнодействующая этих сил «похожа» на силу упругости тем, что она пропорциональна величине смещения и направлена к положению равновесия, но сила не имеет упругой природы. Силу называют квазиупругой силой. Колебательные движения математического маятника можно рассматривать как часть вращательного. Для его описания применим основной закон вращательного движения

, (9)

где M – момент возвращающей силы;

I – момент инерции материальной точки;

e

– угловое ускорение.

При условии малых колебаний заменим ; , x – смещение точки от положения равновесия.

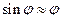
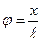
Подставим полученные выражения в формулу

Знак « – » имеет то же значение, что и в случае (6)

или

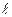
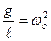
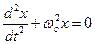
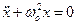
Поделив все члены на , перенеся их в одну сторону, обозначив , получим окончательный вид дифференциального уравнения гармонических колебаний математического маятника:

или , (10)

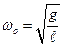
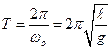
где – собственная частота колебаний;

– период колебаний. (11)

Из формулы (11) видно, что период колебаний математического маятника не зависит от его массы, а определяется лишь его длиной и ускорением свободного падения.

Решением уравнения (10) является уравнение (1).

Рассмотрим физический маятник – это абсолютно твердое тело, которое может свободно вращаться вокруг оси О, не проходящей через его центр масс (рис. 3).

На физический маятник действует сила тяжести 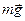и сила реакции опоры . При отклонении физического маятника от положения равновесия на угол j, равнодействующая этих сил является квазиупругой возвращающей силой

Колебания физического маятника рассматриваем как часть вращательного движения вокруг оси О и для его описания применяем основное уравнение динамики вращательного движения

,

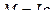
где М – момент возвращающей силы;

I – момент инерции твердого тела, относительно оси О;

e – угловое ускорение.

Знак « – » имеет тот же смысл, что и в случае (6)

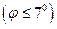
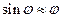
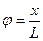
В случае малых колебаний заменим , , х – смещение маятника от положения равновесия.

Сделав подстановку, получили

или

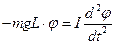
Поделив все члены равенства на , перенесем в одну сторону и обозначим , получим

или (12)

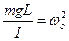
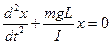
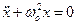
дифференциальное уравнение гармонических колебаний физического маятника.

– собственная частота колебаний

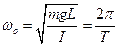
Период колебаний физического маятника выражается формулой

(13)

Приведенной длиной физического маятника называется длина такого математического маятника, у которого его период колебаний совпадает с периодом колебаний данного физического маятника.

(14)

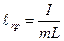
Решением уравнения (12) является уравнение (1).

Итак, гармонические колебания, возникающие в идеальных колебательных системах, не зависимо от вида маятника, описываются одинаковыми уравнениями (7), (10), (12), которые имеют решение (1).

В реальных колебательных системах всегда присутствуют силы трения, на преодоление которых будет тратиться собственная энергия системы. Если энергия не будет восполняться за счет работы внешних сил, то колебания будут затухать, т.е. амплитуда их будет уменьшаться с течением времени.

При малых смещениях от положения равновесия на систему будут действовать:

1) квазиупругая возвращающая сила ;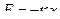

2) сила сопротивления, пропорциональная скорости и направленная противоположно ее направлению ,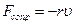

где r – коэффициент сопротивления.

Применим второй закон Ньютона к описанию движения колеблющейся системы

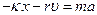
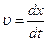
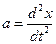
В проекции на ось ОХ, это уравнение будет выглядеть как , если подставить и , получим

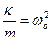
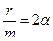
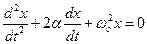
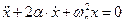
Поделив все члены равенства на m, перенеся их в одну сторону, обозначив , , получим дифференциальное уравнение затухающих колебаний.

или (15)

Решением уравнения (15) будет периодическая функция с убывающей амплитудой

, (16)

где A_o – наибольшее отклонение системы от положения равновесия;

– коэффициент затухания;

– закон убывания амплитуды;

– частота затухающих колебаний.

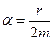
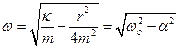
Уменьшение амплитуды колебаний за один период характеризует декремент затухания

В качестве меры затухания берут величину натурального логарифма декремента затухания

(17)

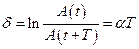
d называют логарифмическим декрементом затухания.

Для получения незатухающих колебаний необходимо воздействовать на систему дополнительной переменной внешней силой, работа которой непрерывно восполняла бы убыль энергии из-за наличия сил трения. Эта переменная сила называется вынуждающей, а колебания – вынужденными.

Пусть вынуждающая сила меняется по гармоническому закону

При этом условии уравнение второго закона Ньютона в случае вынужденных колебаний будет иметь вид

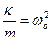
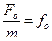
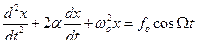
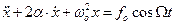
Поделим все члены равенства на m, обозначим ; , , получим дифференциальное уравнение вынужденных колебаний

или (18)

Решением этого уравнения является уравнение вида:

, (19)

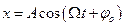
где амплитуда установившихся колебаний имеет вид

,

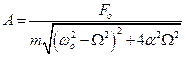
а начальная фаза может быть определена из условия

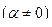
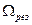
Амплитуда колебаний зависит от частоты вынуждающей силы. Если затухание существует , то амплитуда колебаний достигнет наибольшего значения при частоте вынуждающей силы, совпадающей с частотой незатухающих колебаний w_о:

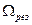
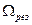
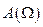
Явление возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к значению называется резонансом. Соответственно величина называется резонансной циклической частотой, а кривые зависимости – резонансными кривыми (рис. 5).

Форма резонансных кривых зависит от величины коэффициента затухания a. С увеличением a резонансные кривые становятся более пологими, уменьшается значение максимума амплитуды

Рис. 5

Описание установки и метода измерений

Прибор для изучения законов колебательного движения представляет собой комбинацию двух связанных маятников: физического 1 и математического 2 (рис.6). Связь маятников осуществляется при помощи вилки 3, жестко связанной с физическим маятником, в ушко которого продернута нить математического маятника. Длина математического маятника может быть измерена на требуемую величину путем перемещения нити с помощью фиксируемого ползунка 4, закрепленного на линейке 5. Положение ползунка на

этой линейке позволяет задать необходимую длину математического маятника. Амплитуда колебаний обоих маятников определяется по шкале 6.

Для увеличения затухания на физическом маятнике может быть закреплена тормозящая пластина 7.

Порядок выполнения и обработка результатов измерений

1. Определение логарифмического декремента затухания

1. Убирают математический маятник (для этого можно поднять шарик или отвести его в сторону).

2. На физическом маятнике закрепляют тормозящую пластину 7.

3. Отклоняют физический маятник до заданной начальной амплитуды A_o, отпускают его и одновременно включают секундомер. Фиксируют число полных колебаний n и промежуток времени t, по прошествии которого амплитуда принимает значение A_n.

4. Полученные результаты заносят в табл. 1.

5. Определяют период T физического маятника по формуле ,

где t – время, n – число полных колебаний.

6. Вычисляют логарифмический декремент затухания по формуле:

и коэффициент затухания по формуле:

7. Вычисляются относительные и абсолютные погрешности при определении d и a. Все результаты заносятся в табл. 1.

A_o – начальная амплитуда; A_n – конечная амплитуда;

n – число колебаний; t – время колебаний;

Т – период колебаний; a – коэффициент затухания;

d – логарифмический декремент затухания.

2. Снятие резонансной кривой

1. Выводят из зацепления математический маятник.

2. Устанавливают начальную длину математического маятника (максимальную или минимальную).

3. Отводят физический маятник на 5 – 6 делений от положения равновесия и дают ему свободно качаться.

Наблюдая возникновение колебаний математического маятника, фиксируют по шкале 6 максимальное значение угла отклонения при заданной длине маятника и заносят в табл. 2 результаты.

4. Изменяя длину маятника последовательно на 10 см, повторяют опыт, проходя весь интервал возможных длин. На участке, где начинает обнаруживаться явление резонанса, изменение длины уменьшают до 5 см. Заносят показания в табл. 2.

5. Строят график зависимости угла отклонения математического маятника от его длины . По графику определяют резонансное значение и сравнивают его величину с – приведенной длиной физического маятника, определяемой по формуле:

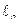
с использованием численного значения T по результатам предыдущего опыта.

Делаются соответствующие выводы.

, м.

, дел.

1. Что мы называем математическим, физическим маятником?

2. Напишите уравнение гармонических колебаний.

3. Выведите дифференциальное уравнение затухающих колебаний.

4. Выведите период колебаний математического и физического маятников.

5. Дайте определение логарифмического декремента затухания. Что характеризует логарифмический декремент затухания?

6. Выведите дифференциальное уравнение вынужденных колебаний.

7. Дайте объяснение явления механического резонанса.

Источник