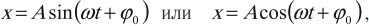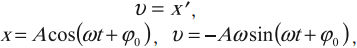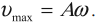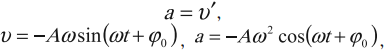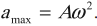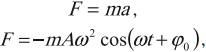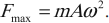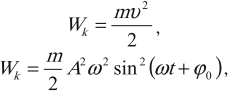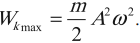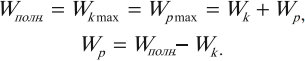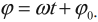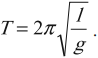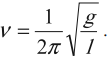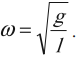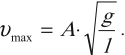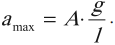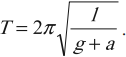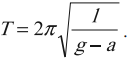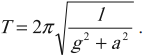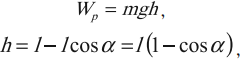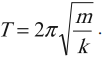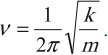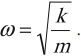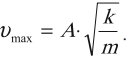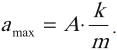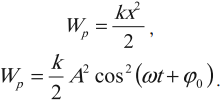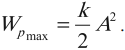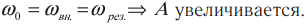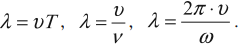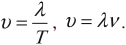Что называют колебаниями механическими колебаниями по каким признакам классифицировать колебания
Механические колебания
теория по физике 🧲 колебания и волны
Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.
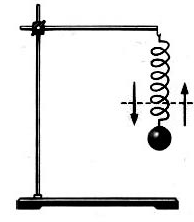
Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.
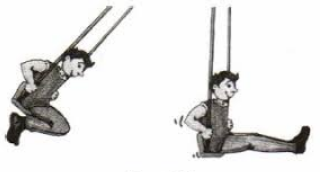
Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.
Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.
Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.
Какими бывают колебания?
Напомним, что в механической системе выделяют два вида сил:
Свободные колебания
Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.
Колебательная система — механическая система, в которой возможно совершение свободных колебаний.
Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:
Примеры свободных колебаний:
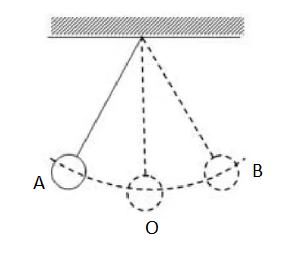
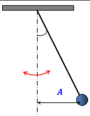
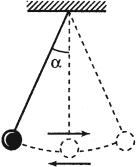
Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.
В колебательную систему математического маятника входят:
В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.
Вынужденные колебания
Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.
Примерами вынужденных колебаний служат:
Затухающие и незатухающие колебания
Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.
Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.
Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.
Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.
Динамика колебательного движения
Для того чтобы описать количественно колебания тела пол действием силы упругости пружины или колебания шарика, подвешенного на нити, воспользуемся законами механики Ньютона.
Уравнение движения тела, колеблющегося под действием сил упругости
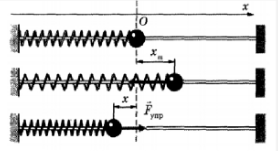
Рассмотрим колебательное движение шарика, вызванное силой упругости, возникшей при растяжении горизонтальной пружины вдоль оси Ох.
Согласно II закону Ньютона произведение массы тела на ускорение равно равнодействующей всех сил приложенных к телу. Поскольку сила трения пренебрежимо мала, мы можем считать, что в этой механической системе действует единственная сила — сила упругости. Учтем, что шарик колеблется вдоль одной прямой, и выберем одномерную систему координат Ох. Тогда:
Согласно закону Гука, проекция сила упругости прямо пропорциональная смещению шарика из положения равновесия (точки О). Смещение равно координате x шарика, причем проекция силы и координаты имеют разные знаки. Это связано с тем, что сила упругости всегда направлена к точке равновесия, в то время как расстояние от этой точки во время движения увеличивается в обратную сторону. Отсюда делаем вывод, что сила упругости равна:
где k — жесткость пружины.
Тогда уравнение движения шарики принимает вид:
Пример №1. Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?
Максимальной скорости груз достигнет при максимальном его отклонении от положения равновесия — в нижней точке траектории. Учтем, что тело движется вниз под действием силы тяжести. Но в то же время на него действует сила упругости, которая возникает в пружине и нарастает до тех пор, пока не становится равной по модулю силе тяжести. Применив III закон Ньютона получим:
∣ ∣ ∣ → F т я ж ∣ ∣ ∣ = ∣ ∣ ∣ → F у п р ∣ ∣ ∣
где y m a x — максимальное отклонение груза от положения равновесия. В этой точке скорость тела будет максимальная. Для нахождения этой величины используем формулу из кинематики:
Начальная скорость равна нулю. Отсюда:
Максимальная скорость равна:
Уравнение движения математического маятника
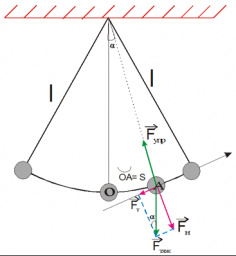
Ниже на рисунке представлен математический маятник. Если мы выведем из положения равновесия шарик и отпустим, возникнет две силы:
При колебаниях шарика также будет возникать сила сопротивления воздуха. Но так как она очень мала, мы будем ею пренебрегать.
Чтобы описать динамику движения математического маятника, удобно силу тяжести разложить на две составляющие:
Причем компонента → F τ направлена перпендикулярно нити, а → F n — вдоль нее.
Компонента → F τ представляет собой проекцию силы тяжести в момент, когда нить маятника отклонена от положения равновесия (точки О) на угол α. Следовательно, она равна:
Знак «–» мы здесь поставили по той причине, что компоненты силы тяжести → F τ и α имеют противоположные знаки. Ведь если отклонить шарик на угол α>0, то составляющая → F τ будет направлена в противоположную сторону, так как она будет пытаться вернуть шарик в положение равновесия. И ее проекция будет отрицательной. Если же шарик отклонить на угол α → F τ будет направлена в обратную сторону. В этом случае ее проекция будет положительной.
Разделим обе части выражения на массу шарика m и получим:
Внимание! Чтобы перевести градусы в радианы, нужно умножить градусы на число π и поделить результат на 180. К примеру 2 о = 2∙3,14/180 рад., или 2 о = 0,035 рад.
При малом отклонении также дугу ОА мы можем принять за длину отрезка OA, который мы примем за s. Тогда угол α будет равен отношению противолежащего катета (отрезка s) к гипотенузе (длине нити l):
Это уравнение похоже на то уравнение, которое мы получили для описания колебательного движения шарика под действием силы упругости. И оно также позволяет сделать вывод, что ускорение прямо пропорционально координате.
При отклонениях на малый угол мы можем пользоваться следующей формулой:
Чтобы найти длину нити, нужно выразить угол α в радианах:
Тогда длина нити равна:
Основные характеристики колебательного движения
Амплитуда — максимальное отклонение тела от положения равновесия. Обозначается буквой A, иногда — xmax. Единиц измерения — метр (м).
Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с).
Период и частота колебаний связаны между собой следующей формулой:
Период колебаний также можно вычислить, зная количество совершенных колебаний N за время t:
Поскольку частота — это величина, обратная периоду колебаний, ее можно выразить в виде:
Пример №3. Определить частоту колебаний груза, если суммарный путь, который он прошел за 2 секунды под действием силы упругости, составил 1 м. Амплитуда колебаний равна 10 см.
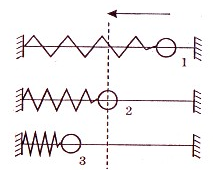
Во время одного колебания груз проходит расстояние, равное 4 амплитудам. Посмотрите на рисунок. Положение равновесия соответствует состояние 2. Чтобы совершить одно полное колебание, сначала груз отводят в положение 1. Когда его отпускают, он проходит путь 1–2 и достигает положения равновесия. Этот путь равен амплитуде колебаний. Затем он продолжает движение до состояния 3. И в это время он проходит расстояние 2–3, равное еще одной амплитуде колебаний. Чтобы вернуться в исходное положение (состояние 1), нужно снова проделать путь в обратном направлении: сначала 3–2, затем 2–1.
Следовательно, количество колебаний равно отношению пройденного пути к амплитуде, помноженной на 4:
Так как мы знаем, что эти колебания совершались в течение 2 секунд, для вычисления частоты мы можем использовать формулу:
В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.
Каков период колебаний шарика?
Алгоритм решения
Решение
Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:
T = 2 ( t 2 − t 1 ) = 2 ( 3 − 1 ) = 4 ( с )
pазбирался: Алиса Никитина | обсудить разбор | оценить
Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остается растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличивается |
| 2) | уменьшается |
| 3) | не изменяется |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Потенциальная энергия пружины определяется формулой:
где k — коэффициент жесткости пружины, а x — ее удлинение. Величина x была максимальной в нижней точке траектории. Когда пружина начинает сжиматься, она уменьшается. Так как потенциальная энергия зависит от квадрата x прямо пропорционально, то при уменьшении этой величины потенциальная энергия пружины тоже уменьшается.
Кинетическая энергия тела определяется формулой:
В нижней точке траектории скорость шарика была равна нулю. Но к этому времени потенциальная энергия пружины достигла максимума. Она начинает с ускорением поднимать шарик вверх, сжимаясь. Следовательно, скорость растет. Так как кинетическая энергия зависит от квадрата скорости тела прямо пропорционально, то при увеличении скорости этой величины кинетическая энергия шарика тоже увеличивается.
Потенциальная энергия тел в поле тяжести земли определяется формулой:
Масса и ускорение свободного падения шарика — постоянные величины. Следовательно, потенциальная энергия зависит только от расстояния до поверхности земли. Когда пружина поднимает шарик, расстояние между ним и землей увеличивается. Так как потенциальная энергия зависит от расстояния прямо пропорционально, то при его увеличении потенциальная энергия шарика тоже растет.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.
Б) Период колебаний шарика равен 4,0 с.
В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.
Г) Амплитуда колебаний шарика равна 30 мм.
Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.
Алгоритм решения
Решение
Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.
Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.
Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.
Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.
Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
Для существования механических колебаний необходимо:
Механические волны – это процесс распространения колебаний в упругой среде.
Виды волн
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где \( x \) – координата тела – смещение тела от положения равновесия в данный момент времени; \( A \) – амплитуда колебаний; \( \omega t+\varphi_0 \) – фаза колебаний; \( \omega \) – циклическая частота; \( \varphi_0 \) – начальная фаза.
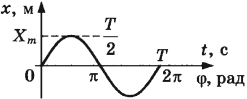
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где \( v \) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где \( a \) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где \( F \) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где \( W_k \) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
При максимальном отклонении от положения равновесия:
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
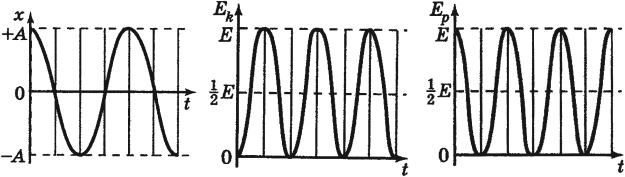
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – \( A\, (X_
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – \( \varphi \) , единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
\( \varphi_0 \) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – \( T \) , единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – \( \omega \) , единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
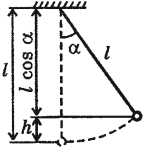
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту \( h \) , определяется по формуле:
где \( l \) – длина нити, \( \alpha \) – угол отклонения от вертикали.
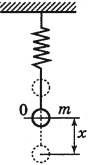
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
\( v_0 \) – собственная частота колебаний маятника.
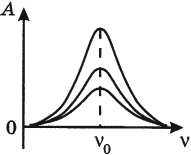
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
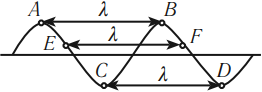
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – \( \lambda \) , единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.