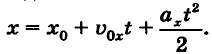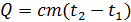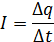Что называют информационными моделями построенными с использованием математических формул и понятий
§1.2 Знаковые модели
1.2.1. Словесные модели
Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках.
Например, гелиоцентрическая модель мира, которую предложил Коперник, словесно описывалась следующим образом:
Множество словесных моделей содержится в ваших школьных учебниках: в учебнике истории представлены модели исторических событий, в учебнике географии — модели географических объектов и природных процессов, в учебнике биологии — модели объектов животного и растительного мира.
Произведения художественной литературы — это тоже модели, так как они фиксируют внимание читателя на определённых сторонах человеческой жизни. Анализируя литературное произведение, вы выделяете в нём объекты и их свойства, отношения между героями, связи между событиями, проводите параллели с другими произведениями и т. п. Самое непосредственное отношение к понятию модели имеет такой литературный жанр, как басня. Смысл этого жанра состоит в переносе отношений между людьми на отношения между вымышленными персонажами, например животными.
Такие особенности естественного языка, как многозначность, использование слов в прямом и переносном значении, синонимия, омонимия и т. п., придают человеческому общению выразительность, эмоциональность, красочность. Вместе с тем наличие этих особенностей делает естественный язык непригодным для создания информационных моделей во многих сферах профессиональной деятельности (например, в системах «человек — компьютер»).
1.2.2. Математические модели
Основным языком информационного моделирования в науке является язык математики.
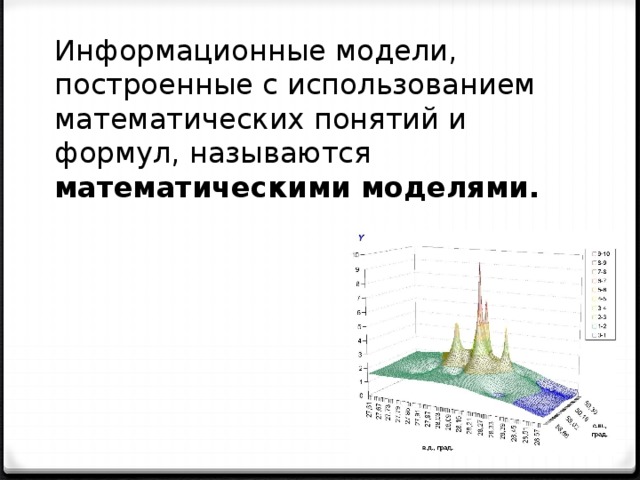
Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.
Язык математики представляет собой совокупность множества формальных языков; с некоторыми из них (алгебраическим, геометрическим) вы познакомились в школе, другие сможете узнать при дальнейшем обучении.
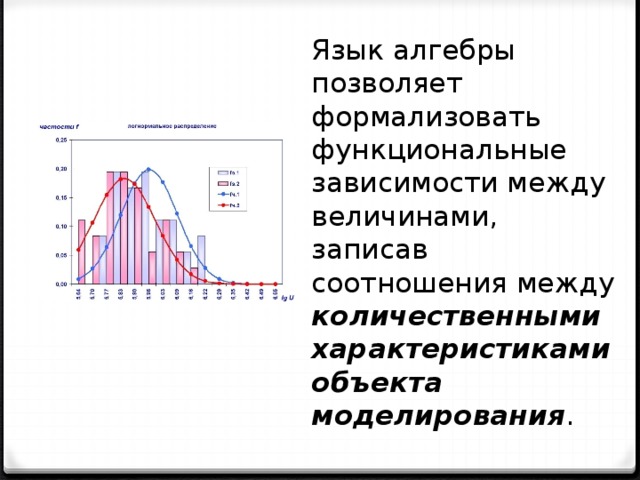
Язык алгебры позволяет формализовать функциональные зависимости между величинами, записав соотношения между количественными характеристиками объекта моделирования. В школьном курсе физики рассматривается много функциональных зависимостей, которые представляют собой математические модели изучаемых явлений или процессов.
Модель оптимизации расходов/доходов
С помощью языка алгебры логики строятся логические модели — формализуются (записываются в виде логических выражений) простые и сложные высказывания, выраженные на естественном языке. Путём построения логических моделей удаётся решать логические задачи, создавать логические модели устройств и т. д.
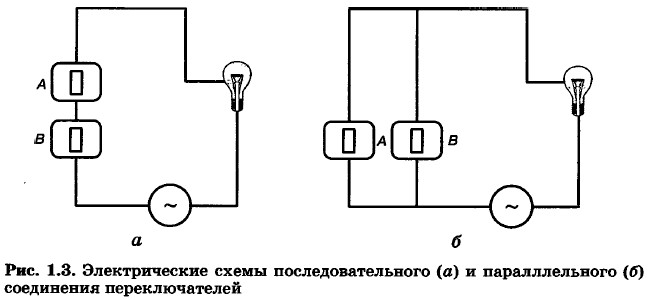
Электрические схемы
1.2.3. Компьютерные математические модели
Многие процессы, происходящие в окружающем нас мире, описываются очень сложными математическими соотношениями (уравнениями, неравенствами, системами уравнений и неравенств). До появления компьютеров, обладающих высокой скоростью вычислений, у человека не было возможности проводить соответствующие вычисления, на счёт «вручную» уходило очень много времени.
В настоящее время самые сложные математические модели могут быть реализованы на компьютере. При этом используются такие средства, как:
— специализированные математические пакеты и программные средства для моделирования.
Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями.
Средства компьютерной графики позволяют визуализировать результаты расчётов, получаемых в процессе работы с компьютерными моделями.
Особый интерес для компьютерного математического моделирования представляют сложные системы, элементы которых могут вести себя случайным образом. Примерами таких систем являются многочисленные системы массового обслуживания: билетные кассы, торговые предприятия, ремонтные мастерские, служба скорой помощи, транспортные потоки на городских дорогах и многие другие модели. Многим знакома ситуация, когда, придя в кассу, магазин, парикмахерскую, мы застаём там очередь. Приходится либо вставать в очередь и какое-то время ждать, либо уходить, т. е. покидать систему необслуженным. Возможны случаи, когда заявок на обслуживание в системе мало или совсем нет; в этом случае она работает с недогрузкой или простаивает. В системах массового обслуживания количество заявок на обслуживание, время ожидания и точное время выполнения заявки заранее предсказать нельзя — это случайные величины.
Имитационные модели воспроизводят поведение сложных систем, элементы которых могут вести себя случайным образом.
Имитационное моделирование — это искусственный эксперимент, при котором вместо проведения натурных испытаний с реальным оборудованием проводят опыты с помощью компьютерных моделей. Для получения необходимой информации осуществляется многократный «прогон» моделей со случайными исходными данными, генерируемыми компьютером. В результате образуется такой же набор данных, который можно было бы получить при проведении опытов на реальном оборудовании или в реальной системе. Однако имитационное моделирование на компьютере осуществляется гораздо быстрее и обходится значительно дешевле, чем натурные эксперименты.
Ссылки на ресурсы ЕК ЦОР
Ссылки на ресурсы ФЦИОР:
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Знаковые информационные модели
§ 10. Знаковые информационные модели
ИНФОРМАТИКА. 6 КЛАССА. БОСОВА Л.Л. ОГЛАВЛЕНИЕ
Ключевые слова:
• словесное описание
• художественное описание
• научное описание
• математическая модель
Словесные описания
Широко распространённой разновидностью знаковых информационных моделей являются словесные описания. Множество словесных описаний содержится в ваших школьных учебниках: в учебнике истории представлены модели исторических событий; в учебнике географии — модели географических объектов и природных процессов; в учебнике биологии — модели объектов животного и растительного мира.
В словесных описаниях ситуации, события, процессы приводятся на естественном языке (русском, английском, немецком и др. — всего на нашей планете более двух тысяч языков).
Словесные описания весьма разнообразны, они могут быть выполнены в разных стилях. Прежде всего, различают разговорный и книжный стили. Книжный стиль имеет такие разновидности как научный, официально-деловой, публицистический, художественный.
Научные описания
Научный стиль используется для передачи точной научной информации. Наиболее важными качествами научного стиля являются логичность и чёткость изложения. В текстах научного стиля присутствует большое количество слов-профессионализмов.
Рассмотрим несколько примеров словесных моделей — научных описаний, содержащихся в ваших школьных учебниках.
Пример 1. Модель римского войска
Пример 2. Модель одноклеточной водоросли хламидомонады
| Тело одноклеточной водоросли хламидомонады имеет все части клетки: оболочку, цитоплазму, ядро, вакуоли, хлоропласт с хлорофиллом и другие органоиды. Вместе с этим у неё есть структуры, свойственные живому организму: жгутики, благодаря которым хламидомонада активно передвигается в водной среде; маленькое красное пятно — глазок в передней части тела, с помощью которого водоросль активно движется в сторону света; две пульсирующие вакуоли, удаляющие из клетки избыточную воду и ненужные вещества.Водоросль питается, дышит, растёт, двигается, размножается, развивается как всякий организм. Вместе с тем её тельце работает как маленькая химическая фабрика, совершая все процессы, свойственные фототрофной клетке. |
Художественные описания
Произведения художественной литературы — это тоже модели, так как они фиксируют внимание читателя на определённых сторонах человеческой жизни. Анализируя литературное произведение, вы выделяете в нём объекты и их свойства, отношения между героями, связи между событиями, проводите параллели с другими произведениями и т. п.
Самое непосредственное отношение к понятию модели имеет такой литературный жанр, как басня. Смысл этого жанра состоит в переносе отношений между людьми на отношения между вымышленными персонажами, например животными.
Пример 3.
Художественный текст мы воспринимаем зрительно. Поэтому для него важна графическая подача. Усилить образность текста можно за счёт его фигурного расположения, смены шрифтов или изменения начертания. Например, в стихотворении Р. Саути «Как падают воды в Лодоре?» (пер. А. Шмульяна) расположение строк вызывает в воображении читателя картину водопада:
| Кипя, Шипя, Журча, Ворча, Струясь, Крутясь, Сливаясь, Вздымаясь, Вздуваясь, Мелькая, шурша, Резвясь и спеша, Скользя, обнимаясь, Делясь и встречаясь, Ласкаясь, бунтуя, летя, Играя, дробясь, шелестя, Блистая, взлетая, шатаясь, Сплетаясь, звеня, клокоча, Взвиваясь, вертясь, грохоча, Морщинясь, волнуясь, катаясь, Бросаясь, меняясь, воркуя, шумя, Взметаясь и пенясь, ликуя, гремя, Дрожа, разливаясь, смеясь и болтая, Катясь, извиваясь, стремясь, вырастая, Вперёд и вперёд убегая в свободолюбивом задоре — так падают бурные воды в сверкающем быстром Лодоре! |
Обратите внимание на важные особенности естественного языка:
* многозначность — разные значения одного многозначного слова сохраняют некоторую общность в толковании их смысла;
* использование слов в прямом и переносном значениях (прямое значение слова переносят на другой предмет);
* синонимия — наличие близких по значению, но разных по звучанию слов;
* омонимия — наличие слов, одинаково пишущихся, но имеющих различное значение и т. д.
С одной стороны, перечисленные особенности делают человеческое общение выразительным, эмоциональным, красочным. С другой стороны, их наличие делает естественный язык непригодным для создания информационных моделей во многих сферах профессиональной деятельности (например, в системах «человек — компьютер»). Именно поэтому наряду с естественными языками используются языки формальные, в которых одинаковые слова всегда имеют одинаковый смысл. С примером формального языка вы познакомитесь чуть позже, при записи программ для исполнителя Чертёжник.
Математические модели
Основным языком информационного моделирования в науке является язык математики.
Модели, построенные с использованием математических понятий и формул, называются математическими моделями.
Пример 4
Рассмотрим текст небольшой заметки из школьной стенгазеты:
| После капитального ремонта бассейн «Дельфин» буквально преобразился: просторные раздевалки и душевые сверкают новеньким кафелем, захватывает дух от вида замысловатой горки и пятиметровой вышки, манит голубая гладь водных дорожек. Но самое главное, строители переделали систему водоснабжения бассейна. Раньше бассейн наполнялся водой из одной трубы. На это уходило 30 часов. Теперь строители подвели ещё одну трубу, которая наполняет бассейн за 20 часов. Представляете, как мало времени теперь потребуется для наполнения бассейна, если включить обе эти трубы! |
Этот текст можно рассматривать как словесную модель бассейна. Попробуем решить содержащуюся в заметке задачу: узнаем, за сколько часов бассейн наполнится водой через обе трубы.
Если отбросить информацию, несущественную с точки зрения поставленной задачи, то условие задачи можно сформулировать так:
| Через первую трубу бассейн наполняется водой за 30 часов, через вторую трубу — за 20 часов. За сколько часов наполнится бассейн, если вода будет поступать через обе трубы одновременно? |
Попробуем решить задачу в общем виде, обозначив время заполнения бассейна через первую и вторую трубы — через А и В соответственно. Примем за 1 весь объём бассейна, искомое время обозначим через t.
Так как через первую трубу бассейн наполняется за А часов, то 1 /А — часть бассейна, наполняемая первой трубой за 1 час; 1 /В — часть бассейна, наполняемая второй трубой за 1 час.
Следовательно, скорость наполнения бассейна первой и второй трубами вместе составит: 1 /А + 1 /В.
Мы получили математическую модель, описывающую процесс наполнения бассейна из двух труб.
Преобразуем выражение в скобках:
Формула (1) примет вид:
Теперь искомое время может быть вычислено по формуле (2):
Несложно подсчитать, что при исходных данных А = 30 и В = 20 искомое время равно 12 часам.
Пример 5
На шоссе расположены пункты А и В, удалённые друг от друга на 20 км. Мотоциклист выехал из пункта В в направлении, противоположном пункту А, со скоростью 50 км/ч (рис. 31).
Вопросы и задания
1. В каком из примеров параграфа использовано больше всего слов-профессионализмов?
3. Вспомните басни И. А. Крылова «Волк и Ягнёнок», «Ворона и Лисица», «Демьянова уха», «Квартет», «Лебедь, Щука и Рак», «Лисица и виноград», «Слон и Моська», «Стрекоза и Муравей», «Тришкин кафтан» и др. Какие черты характера людей и отношения между людьми смоделировал в них автор?
4. Воспользовавшись моделью, построенной в примере 6, определите, за сколько часов бассейн может быть наполнен через первую трубу, если через вторую он заполняется за 24 часа, а через первую и вторую вместе — за 8 часов.
5. Постройте математические модели для приведёных ниже задач. Какой вы можете сделать вывод на основании полученных моделей?
а) Первая бригада может выполнить задание за А дней, а вторая — за Б дней. За сколько дней обе бригады выполнят задание, работая вместе?
б) Два велосипедиста одновременно направились навстречу друг другу из двух сёл. Первый мог бы проехать расстояние между сёлами за А минут, второй — за В минут. Через сколько минут они встретятся?
Математические модели
Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями
Просмотр содержимого документа
«Математические модели»
Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.
Компьютерные математические модели
Многие процессы, происходящие в окружающем нас мире, описываются очень сложными математическими соотношениями (уравнениями, неравенствами, системами уравнений и неравенств).
• специализированные математические пакеты- и программные средства для моделирования.
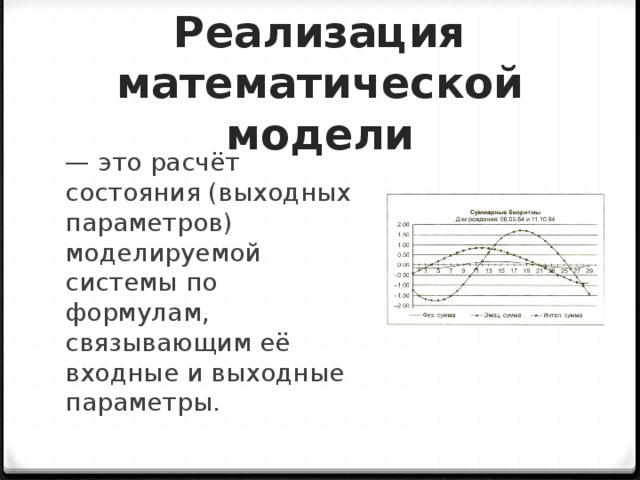
Реализация математической модели
— это расчёт состояния (выходных параметров) моделируемой системы по формулам, связывающим её входные и выходные параметры.
Математические модели
Основным языком информационного моделирования в науке является язык математики.
 Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями. Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями. |
Язык математики представляет собой совокупность множества формальных языков; с некоторыми из них (алгебраическим, геометрическим) вы познакомились в школе, другие сможете узнать при дальнейшем обучении.
Язык алгебры позволяет формализовать функциональные зависимости между величинами, записав соотношения между количественными характеристиками объекта моделирования. В школьном курсе физики рассматривается много функциональных зависимостей, которые представляют собой математические модели изучаемых явлений или процессов.

Изменение координаты тела х при прямолинейном равноускоренном движении в любой момент времени t выражается формулой:
С помощью языка алгебры логики строятся логические модели — формализуются (записываются в виде логических выражений) простые и сложные высказывания, выраженные на естественном языке. Путём построения логических моделей удаётся решать логические задачи, создавать логические модели устройств и т. д.

На них изображены известные вам из курса физики последовательное и параллельное соединения переключателеЗ. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателеЗ. Можно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:
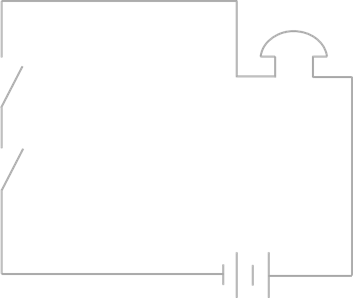
Спроектируем электрическую цепь, показывающую итог таЗного голосования комиссии в составе председателя и двух рядовых членов. При голосовании «за» каждыЗ член комиссии нажимает кнопку. Предложение считается принятым, если члены комиссии проголосуют за него единогласно либо если свои голоса «за» отдадут председатель и один из рядовых членов комиссии. В этих случаях загорается лампочка.
Решение. Пусть голосу председателя соответствует переключатель А, голосам рядовых членов — переключатели В и С. Тогда F(A, B,C) = A & B & C ∨ A & B ∨ A & C.
Упростим полученное логическое выражение:
F(A, В, С) = А & В & (С ∨ 1) ∨ A & C = A & B & 1 ∨ A & C = A & B ∨ A & C = A & (B ∨ С).
Мы получили логическую модель, позволяющую построить схему проектируемой электрической цепи, изображённую на рис. 1.4.
Знаковые модели. Математические модели
Урок 3. Информатика 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Знаковые модели. Математические модели»
Математический язык является основным языком математического моделирования. Математическая модель – это информационная модель, которая построена с использованием математических понятий и формул.
Математический язык состоит из множества формальных языков. Со многими из них вы уже познакомились в школе (например алгебраический и геометрический), некоторые вы узнаете при дальнейшем обучении.
Существуют определённые требования к математическим моделям. Рассмотрим их. Первое требование – универсальность. Это означает, что в модели должны быть полностью отображены все изучаемые свойства реального объекта. Второе. Адекватность. В модели должны быть отражены все нужные свойства объекта с погрешностью не выше заданной. Третье. Точность. Совпадение характеристик реального объекта и значений этих характеристик, полученных с помощью моделей, должны быть максимально точными. Четвёртое требование. Экономичность. Данное требование определяется затратами ресурсов ЭВМ (памяти и времени) на её реализацию и эксплуатацию.
С помощью алгебраического языка можно формализовать функциональные зависимости между количественными характеристиками объекта моделирования. Функциональные зависимости вы можете найти в школьном курсе физики. Они представляют собой математические модели изучаемых процессов или явлений.
Разберёмся на примере. Зависимость количества теплоты при нагревании тела от разности конечной и начальной температуры имеет вид:
Зависимость силы тока от заряда, прошедшего через проводник за единицу времени выглядит следующим образом:
Так же с помощью языка алгебры логики строятся логические модели. При построении логической модели простые и сложные высказывания, выраженные, при помощи естественного языка формализуются, то есть записываются в виде логических выражений. При построении логических моделей можно решать логические задачи, создавать логические модели устройств и так далее.
Рассмотрим две электрические схемы соединения переключателей. На первой представлено последовательное соединение, а на второй – параллельное.
Схема последовательного соединения переключателей
Схема параллельного соединения переключателей
На первой схеме, чтобы звонок зазвенел, должны быть включены оба переключателя.
Схема последовательного соединения переключателей
На второй схеме достаточно, чтобы был включён хотя бы один из переключателей.
Схема параллельного соединения переключателей
Давайте проведём аналогию между элементами электрических схем, а также объектами и операциями алгебры логики и изобразим всё это в таблице.