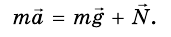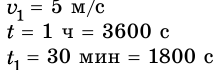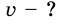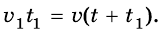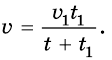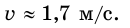Что называют инерциальной системой отсчета

Инерциальные системы отсчета.

Инерциальными системами отсчета называют такие системы, относительно которых все тела, не испытывающие действия сил, движутся равномерно и прямолинейно.

Если какая-либо система отсчета движется относительно инерциальной системы поступательно, но не прямолинейно и равномерно, а с ускорением или же вращаясь, то такая система не может быть инерциальной и закон инерции в ней не выполняется.

Во всех инерциальных системах отсчета все механические и физические процессы протекают совершенно одинаково (при одинаковых условиях).

Согласно принципу относительности, все инерциальные системы отсчета равноправны и все проявления законов физики в них выглядят одинаково, а записи этих законов в разных инерциальных системах отсчета имеют одинаковую форму.

Если в изотропном пространстве существует хотя бы одна инерциальная система отсчета, приходим к выводу, что существует бесконечное множество таких систем, движущихся друг относительно друга поступательно, равномерно и прямолинейно. Если инерциальные системы отсчета существуют, то пространство однородно и изотропно, а время – однородно.

Законы Ньютона и другие законы динамики выполняются только в инерциальных системах отсчета.

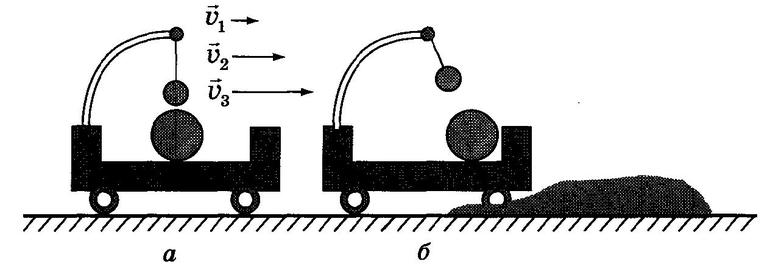
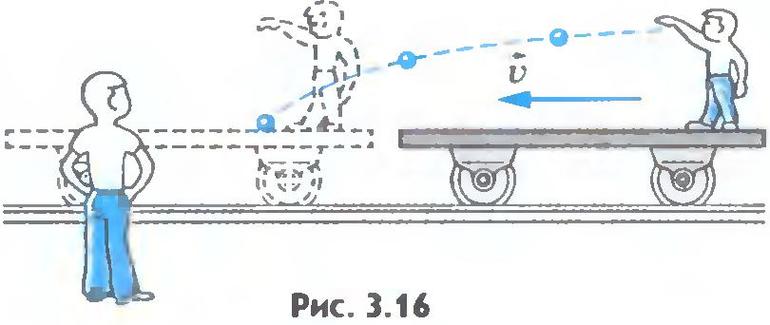
Рассмотрим пример инерциальной и неинерциальной систем. Возьмем тележку, на которой находятся два шарика. Один из них лежит на горизонтальной поверхности, а другой подвешен на нити. Сначала тележка движется относительно Земли прямолинейно и равномерно (а). Силы, действующие на каждый шарик по вертикали, уравновешены, а по горизонтали на шарики никакие силы не действуют (силу сопротивления воздуха можно проигнорировать).

При любой скорости движения тележки относительно земли (υ₁, υ₂, υ₃ и т.д.) шарики будут находиться в покое относительно тележки, главное, чтобы скорость была постоянной.

Однако, когда тележка наедет на песчаную насыпь (б), ее скорость начнет быстро уменьшаться, в результате чего тележка остановится. Во время торможения тележки оба шарика придут в движение – изменят свою скорость относительно тележки, хотя их никакие силы не толкают.

В этом примере первой (условно неподвижной) системой отсчета является Земля. Вторая система отсчета, движущаяся относительно первой – тележка. Пока тележка двигалась равномерно и прямолинейно, шарики находились в покое относительно тележки, т. е. выполнялся закон инерции. Как только тележка стала тормозить, т. е. начала двигаться с ускорением относительно инерциальной (первой) системы отсчета, закон инерции перестал выполняться.

Строго инерциальной системы отсчета нет. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом, по отношению к которому изучается различных объектов. Все реальные тела движутся с каким-либо ускорением, следовательно любая реальная система отсчета может рассматриваться в качестве инерциальной лишь приближенно.

Инерциальной системой с очень высокой степенью точности считается гелиоцентрическая система, связанная с центром Солнца и координатными осями, направленными на три далекие звезды. Эту систему используют в задачах небесной механики и космонавтики. В большинстве технических задач инерциальной системой отсчета считают любую систему, жестко связанную с землей (или любым телом, которое покоится или движется прямолинейно и равномерно относительно поверхности Земли).

Источник

Инерциальная система отсчёта

Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным.

Содержание

Свойства инерциальных систем отсчёта

Всякая система отсчёта, движущаяся относительно ИСО равномерно и прямолинейно, также является ИСО. Согласно принципу относительности, все ИСО равноправны, и все законы физики инвариантны относительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.

Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга со всевозможными постоянными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер, однородность пространства относительно сдвигов даст закон сохранения импульса, изотропность приведёт к сохранению момента импульса, а однородность времени — к сохранению энергии движущегося тела.

Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.

В специальной теории относительности скорости относительного движения ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости «C» (скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца.

Связь с реальными системами отсчёта

С разной степенью точности и в зависимости от области использования инерциальными системами можно считать системы отсчёта, связанные с: Землёй, Солнцем, неподвижные относительно звезд.

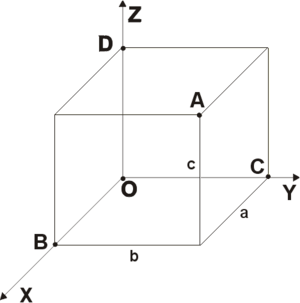
Геоцентрическая инерциальная система координат

Применение Земли в качестве ИСО, несмотря на приближённый его характер, широко распространено в навигации. Инерциальная система координат, как часть ИСО строится по следующему алгоритму. В качестве точки O- начала координат выбирается центр земли в соответствии с принятой её моделью. Ось z – совпадает с осью вращения земли. Оси x и y находятся в экваториальной плоскости. Следует заметить, что такая система не участвует во вращении Земли.

Источник

Содержание:

Инерциальные системы отсчета:

Вы уже знаете, что движение и покой относительны. Если относительно одной системы тело находится в состоянии покоя, то относительно других систем отсчета тело может двигаться. Рассмотрим, например, шайбу, лежащую на ледовой площадке. Шайба находится в покое относительно льда (Земли), потому что влияние на нее Земли компенсируется влиянием льда. Но для хоккеиста, движущегося мимо шайбы прямолинейно и равномерно, она движется прямолинейно и равномерно в противоположную сторону. Таким образом, одно и то же тело (шайба) относительно одной системы отсчета (связанной с Землей) находится в покое, относительно другой (связанной с хоккеистом) движется прямолинейно и равномерно. Но хоккеист ударил по шайбе клюшкой (рис. 276).

В итоге очень непродолжительного действия клюшки шайба начинает двигаться, приобретая некоторую скорость. Интересно, что после удара, когда действие клюшки на шайбу уже прекратилось, шайба продолжает движение. Тем временем после удара влияние на шайбу других тел осталось таким же, как и до удара: как и раньше, действие Земли компенсируется действием льда, а клюшка, как и до удара, никакого влияния на движение шайбы не оказывает. Шайба после удара движется по прямой линии с почти постоянной скоростью, сообщенной ей в момент удара. Но шайба в конце концов остановится, хотя из опыта известно: чем более гладкими будут лед и шайба, тем более длительным будет движение шайбы. Поэтому можно догадаться, что если совсем устранить действие льда на подвижную шайбу (это действие называют трением), то шайба продолжала бы двигаться относительно Земли с постоянной скоростью без остановки.

Этот пример и много других, подобных ему, является проявлением одного из основных законов механики, который называют первым законом движения, или первым законом Ньютона.

Инерциальные системы отсчета

Существуют такие инерциальные системы отсчета, относительно которых тело, движущееся поступательно, сохраняет свою скорость постоянной, если на него не действуют другие тела (или действие других тел уравновешено).

Само явление сохранения скорости движения тела (в частности, состояние покоя) при компенсации внешних действий на тело называют инерцией. Поэтому первый закон Ньютона часто называют законом инерции. Повседневное выражение «движение по инерции» и означает движение тела с постоянной скоростью, когда действие других тел уравновешено.

В первом законе Ньютона речь идет о равномерном прямолинейном движении. Движение мы можем рассматривать только в какой-либо системе отсчета. Возникают вопросы: в какой же системе отсчета выполняется первый закон? Можно ли считать, что он выполняется в любой системе отсчета? Закон инерции выполняется не во всех системах отсчета.

Возникает вопрос: существуют ли строго инерциальные системы? Ньютон, формулируя закон инерции и включая его в основные законы динамики, утверждал этим, что такие системы отсчета в природе существуют. В действительности, если в природе имеет место закон инерции, то должна существовать и такая система отсчета, где он выполняется абсолютно строго, то есть инерциальная система отсчета. А если существует хотя бы одна такая система, то из этого следует, что их есть бесчисленное количество, потому что всякая система отсчета, движущаяся равномерно и прямолинейно относительно инерциальной, будет также инерциальной.

Поскольку сила одна и та же, то какая-то величина должна быть одинакова для всех тел, которые ускоряются этой силой. На опыте и выясним, что это за величина.

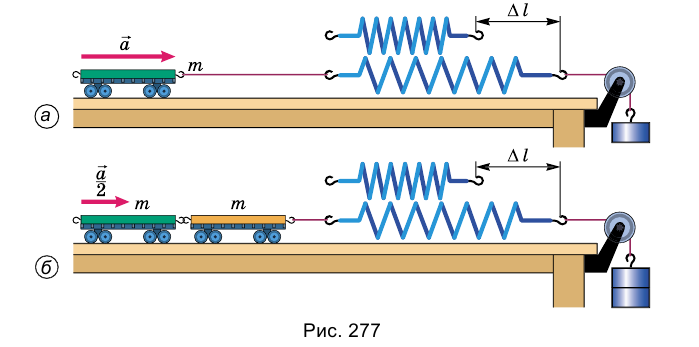
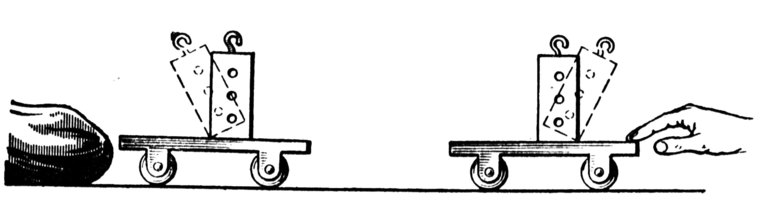
Опыт. К тележке, масса которой известна (т), прикрепим один конец пружины, а второй ее конец прикрепим к нити с грузом, переброшенной через блок (рис. 277, а). Вследствие притягивания к Земле груз движется вниз и растягивает пружину. Она, растянутая на определенную длину Д(, действует силой упругости на тележку и сообщает ему ускорение. Это ускорение можно измерить, например, оно равно а.

Это дало Ньютону основание утверждать, что сила определяется произведением массы тела и его ускорения, и сформулировать важнейший закон механики, который назвали вторым законом Ньютона.

Сила, действующая на тело, определяется произведением массы тела и его ускорения, предоставленного этой силой.

Формулу, выражающую второй закон Ньютона, следует записывать в таком виде: 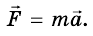Из этой формулы можно получить выражение для

ускорения движения тела 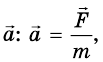из которого видно, что ускорение тела

всегда направлено так же, как и сила, вызывающая его.

Ускорение движения тела прямо пропорционально силе, приложенной к нему, и обратно пропорционально массе тела и направлено в сторону действия силы.
Следует заметить, что второй закон Ньютона, как и первый, выполняется лишь для материальных точек. В случае действия сил на протяженное тело второй закон описывает ускорение не всего тела, а только его центра масс. При поступательном движении тела все его точки имеют одинаковые ускорения. Второй закон выполняется для всех точек.

Силы, с которыми какие-либо два тела действуют друг на друга, всегда равны по модулю и противоположны по направлению.

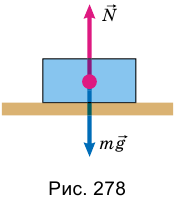
Пусть, например, на столе лежит тело (рис. 278).

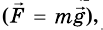
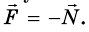
С какой силой оно действует на стол , с такой же по значению силой стол действует на тело N. Математически это записывают так: Знак «-» указывает на противоположность действия этих сил.

Третий закон Ньютона выполняется для подвижных тел

Однако равенство сил не всегда обусловлено третьим законом. Следует различать силы взаимодействия, приложенные к разным взаимодействующим телам, и так называемые равнодействующие силы, которые действуют на одно тело. Силы взаимодействия подчиняются третьему закону Ньютона, а силы, действующие на одно тело, подчиняются второму закону. Чтобы разобраться в этом подробнее, рассмотрим пример.

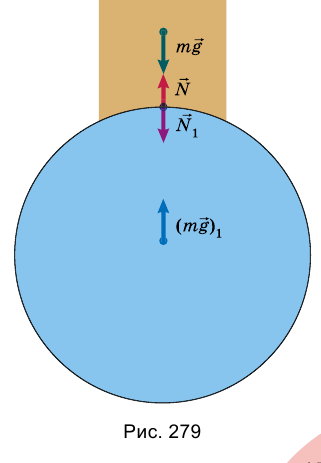
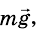
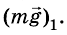
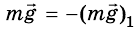
На поверхности Земли лежит тело (рис. 279). На тело действует сила , с которой его притягивает Земля. Но по третьему закону Ньютона и тело притягивает к себе Землю с такой же по значению, но противоположно направленной силой Следовательно, по третьему закону Ньютона.

Кроме гравитационного взаимодействия Земли и тела, между ними существует еще и упругое: с какой силой тело действует на Землю, с такой же силой и Земля действует на тело, то есть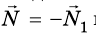по третьему закону Ньютона.

Таким образом, на тело действуют две силы: mg и N. Для этих сил, поскольку они приложены к одному телу, можно записать второй закон Ньютона:

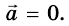
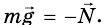
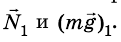
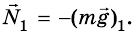
Тело находится в покое, то есть Поэтому Это равенство сил доказано на основе второго закона Ньютона. На Землю также действуют две силы: Они уравновешены, то есть Это равенство так же является следствием применения второго закона.

Пример задачи с решением

Велосипедист движется со скоростью 5 м/с. С какой скоростью двигался пешеход, вышедший из того же места на 1 час раньше, если велосипедист догнал его через 30 мин после начала своего движения?

Дано:

Решение:

Велосипедист и пешеход преодолели одинаковое расстояние, следовательно:

сюда:

Подставим значение известных величин и по-

лучим: и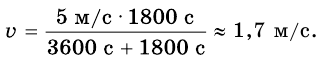
Ответ:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Что такое инерциальная система отсчета?

Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.

Как установить, что данная система отсчета является инерциальной? Это можно сделать только опытным путем. Наблюдения показывают, что с очень высокой степенью точности можно считать инерциальной системой отсчета гелиоцентрическую систему, у которой начало координат связано с Солнцем, а оси направлены на определенные «неподвижные» звезды. Системы отсчета, жестко связанные с поверхностью Земли, строго говоря, не являются инерциальными, так как Земля движется по орбите вокруг Солнца и при этом вращается вокруг своей оси. Однако при описании движений, не имеющих глобального (т. е. всемирного) масштаба, системы отсчета, связанные с Землей, можно с достаточной точностью считать инерциальными.

С гораздо большей точностью можно считать инерциальной систему отсчета, в которой начало координат совмещено с центром Солнца, а координатные оси направлены к неподвижным звездам. Эту систему отсчета называют гелиоцентрической.

Инерциальными являются и системы отсчета, которые движутся равномерно и прямолинейно относительно какой-либо инерциальной системы отсчета.

Галилей установил, что никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномерно и прямолинейно. Это утверждение носит название принципа относительности Галилея или механического принципа относительности.

Этот принцип был впоследствии развит А. Эйнштейном и является одним из постулатов специальной теории относительности. Инерциальные системы отсчета играют в физике исключительно важную роль, так как, согласно принципу относительности Эйнштейна, математическое выражение любою закона физики имеет одинаковый вид в каждой инерциальной системе отсчета. В дальнейшем мы будем пользоваться только инерциальными системами (не упоминая об этом каждый раз).

Источник

Краткие сведения про особенности системы

В системах отсчёта (СО), построенных в соответствии с типом инерции, свободные тела движутся прямым и измеренным образом — с недоступностью внешнего воздействия или вообще не двигаются. В этой СО место считается однородным и изотропным. Термин ИСО был придуман Людвигом Ланге в 1885 году для обозначения системы координат, в которой используются законы Ньютона и формулы расчёта.

Движение тела должно учитываться в сравнительно разных частях, в противном случае невозможно определить состояние его на месте. Наконец, говоря про инерциальное явление, следует показать, относительно чего тело будет в спокойном состоянии или движется размеренно и прямо.

Таким образом, по первому закону Ньютона, именуемому инерционным, формулируют данные описанным образом. Есть такие высокие классы, в отношении которых прогрессивно передвигаемые тела защищают долгосрочную скорость, если влияние иных на него компенсируется. При ИСО тело движется в постоянном значении. Таким образом, движение тела в СО происходит с одинаковой степенью скорости.

Системы отсчёта можно отнести к инерциальным те:

Во всех ИСО с одинаковыми начальными критериями механические явления проходят одинаково, то есть подчиняются одному и тому же закону. Это утверждение называется принципом относительности Галилея.

Инерционный и неинерционный вид

СО, для которых есть закон инерции, называются инерционными. Галилеевские эксперименты фактически рекомендовали считать СО, связанную с территорией, инерциальной. Но ИС бесконечны. Каждая СО, движущаяся с постоянной скоростью относительно другой, считается инерциальной. В них ускорение тела станет похожим.

Если СО перемещается относительно и понемногу, но с переменной скоростью или оборотами, то она не считается инерционной. В такой системе тело обладает способностью самостоятельно ускоряться, в том числе если другие части её не поражены. В неинерциальных системах отсчёта первый закон Ньютона не выполняется.

В настоящем времени известно, что сама справочная система, связанная с территорией, обладает способностью быть приблизительно инерциальной. Кропотливые исследования говорят, что на самом деле, когда тела перемещаются относительно СО, связанной с территорией, появляются нарушения закона инерции. С гораздо большей точностью примерами инерциальной системы отсчёта можно считать те, что связаны с Солнцем и другими звёздами.

Как известно, территория движения относительна звёздному небу, а солнце ускоряется и вращается вокруг своей оси. Но если закон инерции нарушается в системах отсчёта, связанных с территорией, в задачах изучения предусмотрены небольшие перемещения, и в результате этого, как правило, СО, связанные с территорией, считаются инерционными.

В настоящее время есть системы позиционирования тела, которые включают устройство для измерения времени и систему координат. В зависимости от того, движется ли тело или неподвижно, можно охарактеризовать состояние объекта в нужное время.

Основные информационные данные

Инерциальная навигационная система (модули) — это безопасный способ получения информации о курсе, координатах, скорости и параметрах выравнивания угла с платформы, на которой она установлена. После этого стоит отметить такие существенные особенности, как автономность и отсутствие маскирующих видов работ, которые определяют их широкую реализацию. Основа традиционной (ньютоновской) законодательной механики.

Начальный геоцентрический (первичный) аппарат, по сравнению с которым проводятся измерения, считается инерционным (то есть безусловным, фиксированным относительно звезд). При его поддержке объекты выравниваются по координатам, скорости, ускорению и другим ключевым характеристикам (самолеты, ракеты, галактические, подводные лодки и так далее).

Модули ИНС имеют явные высокие качества по сравнению с другими навигационными системами:

Использование навигации

ИСО предоставляет данные навигации для пользовательских систем. Она использует силу и кольцевой лазерный гироскоп вместо обычного определения угловой скорости относительно осей. Её датчики установлены непосредственно на планере. Основная функция каждого датчика состоит в жестком определении и расчёте линейных ускорений и угловых скоростей вращения относительно существующих осей движения летательного аппарата.

Эти данные используются для отображения навигации. Каждый датчик может рассматриваться и содержит три лазерных гироскопа и три акселерометра. Они воспринимают угловые скорости и линейные ускорения соответственно. Полученные данные преобразуются в локальные вертикальные координаты и объединяются с входной информацией эфира для расчёта важных параметров, применимость для:

Выходы ИС могут бывать на дисплеях системы бортового приборостроения. Они также отображаются на дисплее управления полётом.

Общие положения

Первое требование, которое должно выполняться ИС, чтобы работать нужным образом, является выравниванием границ. Оно в основном состоит из определения локальной вертикали и начального курса. В расчётах выравнивания используется основная предпосылка, что единственные ускорения обусловлены силой тяжести земли. Одно движение во время выравнивания, значит, вращение.

Ускорения, вызванные гравитацией, всегда перпендикулярны поверхности и, таким образом, определяют локальную вертикаль. Она используется для установки данных об ориентации так, чтобы они были точно привязаны к вертикали.

После того как причина установлена, лазерный гироскоп определяет компоненты скорости Земли, чтобы знать курс самолёта. По мере того как выравнивание продолжается, определения вертикальной привязки и рубрики настраиваются для максимальной точности.

Минимальная продолжительность режима выравнивания составляет 10 минут. При навигации ИС предоставляют выходные данные для ориентации, курса, текущего положения, ускорений, угла смещения, скорости относительно Земли и данных о ветре. Эти гелиоцентрические выходы все выводятся из данных гироскопического датчика и акселерометра. Начальные сигналы ориентации могут немного существовать, а курс и скорости модифицируются сигналами датчиков, чтобы входить в реальном времени в текущие поступательные параметры посредством реализации и вычислений компьютера.

Источник