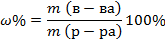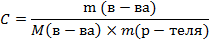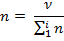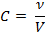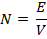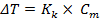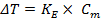Что называют энтропией химической реакции
Энтропия и ее изменение при химических реакциях
Чтобы определить, протекает ли химическая реакция самопроизвольно, необходимо знать движущие силы самопроизвольных процессов.
Одной из движущих сил химической реакции является уменьшение энтальпии системы, т.е. экзотермический тепловой эффект реакции. Опыт показывает, что большинство самопроизвольных процессов являются экзотермическими, т.е. сопровождаются выделением теплоты (ΔН 0, т.е. эндотермические, которые, тем не менее, протекают самопроизвольно, например, растворение некоторых солей (КСl, NН4Сl и др.) в воде.
Следовательно, имеется и другая движущая сила самопроизвольных процессов, не связанная с энтальпией. Это стремление частиц (молекул, ионов, атомов) к хаотическому движению, а системы — к переходу из более упорядоченного состояния к менее упорядоченному.
Тенденцию к неупорядоченности характеризует величина, которую называют энтропия. Итак, энтропия — термодинамическая функция, которая является мерой неупорядоченности в системе.
В качестве примера рассмотрим систему из двух газов, не реагирующих между собой, например, аргона и гелия, которые разделены перегородкой и находятся при одинаковой температуре и давлении.
Удалим перегородку, не изменяя энергетического запаса системы. Назовем это (исходное) состояние системы состоянием 1.
Несмотря на одинаковые давления газов, начнется процесс смешения и через некоторое время молекулы гелия и аргона будут равномерно распределены по всему объему системы. Новое (конечное) состояние системы назовем состоянием 2.
Опыт и теоретические расчеты показывают, что два газа, не разделенные перегородкой, всегда смешиваются, вероятность состояния 1 ничтожно мала. Состояние 2 равномерного распределения обоих газов является наиболее вероятным. Точно также при растворении сахара в воде наиболее вероятным будет состояние равномерного распределения молекул сахара в воде, а исходное состояние (отдельно сахар, отдельно вода) является наименее вероятным. Движущей силой смешения газов или растворения сахара является тенденция перехода в наиболее вероятное состояние.
Энтропия S — логарифмическое выражение вероятности состояния системы. S = k·lnW,
где k — постоянная Больцмана, равная отношению молярной газовой постоянной R к числу Авогадро NА: k = R/NА = 1,38·10 —23 Дж/К.
W— термодинамическая вероятность состояния системы, равная числу микросостояний, при помощи которых осуществляется данное макросостояние.
Это соотношение называется формулой Больцмана. Формула Больцмана позволяет теоретически рассчитать энтропию системы по числу возможных ее микросостояний. Такие расчеты хорошо согласуются с экспериментально определенными величинами.
Как и все термодинамические функции, энтропия является аддитивной функцией, т. ее величина пропорциональна размерам системы (массе, объему). Общепринятая размерность энтропии: Дж/моль·К.
Энтропия вещества в стандартном состоянии называется стандартной энтропией S 0 и приводится в справочниках.
В отличие от других термодинамических функций, можно определить не только изменение, но и абсолютное значение энтропии. Это вытекает из высказанного в 1911 г Максом Планком постулата, согласно которому:
При абсолютном нуле энтропия идеального кристалла равна нулю.
Этот постулат получил название третьего закона термодинамики.
Число микросостояний кристаллических веществ при температуре 0 К невелико. W0 ≈ 1. Подставив это значение в выражение S = k·lnW, получаем S0 = 0
По мере повышения температуры растет скорость различных видов движений частиц, т.е. число их микросостояний. Соответственно растет термодинамическая вероятность и энтропия вещества. При переходе вещества из твердого состояния в жидкое значительно увеличивается неупорядоченность и возрастает энтропия (ΔSПЛ). Особенно резко возрастает энтропия вещества при его переходе из жидкого состояния в газообразное (ΔSКИП).
Так, для воды: S 0 КР = 45,99, S 0 Ж = 70,08 и S 0 ГАЗ = 188,7 Дж/моль·К.
Вследствие высоких значений энтропий газов, последние называют »носителями энтропии».
Энтропия простых веществ является периодической функцией порядкового номера элемента. Увеличение числа атомов в молекуле приводит к увеличению энтропии. Например:
S 0 (О) = 161, S 0 (О2) = 205 и S 0 (О3) = 298,8 Дж/моль·К.
Итак, энтропия возрастает с увеличением движения частиц: при нагревании, испарении, плавлении, расширении газов, при увеличении размеров молекул вещества. Процессы, связанные с упорядочением системы: охлаждение, конденсация, кристаллизация, сжатие, уменьшение объема газов в реакции и т.д. — ведут к уменьшению энтропии.
Изменение энтропии в ходе химической реакции можно оценить без расчета, если в ходе реакции изменяется объём газов. Например:
Наука выделяет в особый класс изолированные системы. В них можно прогнозировать направление самопроизвольного протекания процесса только по изменению энтропии, используя второй закон термодинамики, который гласит: в изолированных системах самопроизвольно протекают только такие процессы, которые сопровождаются возрастанием энтропии (ΔS > 0).
Однако реальные системы, в которых протекают химические реакции, не бывают изолированные, так как они всегда обмениваются энергией (или энергией и веществом) с окружающей средой. Для этих систем, т.е. закрытых или открытых, ни изменение энтропии, ни изменение энтальпии по отдельности не может служить критерием самопроизвольности процесса.
Энтропия. Направление химических реакций.
S – энтропия – это термодинамическая функция, являющаяся мерой неупорядоченности системы.
Характеристика состояния, основанная на измерении общих параметров системы, то есть P, V и Т, выражает так называемое макросостояние системы. Характеристика системы, основанная на определении координат и скорости каждой частицы, соответствует микросостоянию системы.
Например, в данном объеме при заданных температуре и давлении находятся 2 частицы. Если принять, что P, V и Т – const, то скорости и координаты частиц могут быть самыми разными, главное, чтобы средняя скорость и геометрически усредненное местоположение их были одинаковы. Таким образом, для одного единственного макросостояния возможно много микросостояний и чем их больше, тем больше беспорядочность в данной системе.
Число микросостояний, обеспечивающих данное макросостояние, называется термодинамической вероятностью состояния.
S [Дж/моль×К] = R×lnW, где W – термодинамическая вероятность.
2 Закон термодинамики: состояние системы, предоставленной самой себе, изменяется в направлении состояния, обладающего максимальной термодинамической вероятностью, то есть в сторону увеличения энтропии.
Вторая формулировка: теплота не может сама переходить от холодного тела к горячему. Рисунок.
Энтропия единственная термодинамическая функция, для которой можно измерить ее абсолютное значение. При температуре абсолютного нуля энтропия идеального кристалла равна нулю.
Изменение энтропии в ходе химическое реакции определяется по аналогии с законом Гесса:
Энергия Гиббса: G = H – TS или DG = DН – TDS при T = const; P = const.
О направлении химического процесса говорит правило Гиббса: в изолированных закрытых системах принципиально возможно самопроизвольное протекание процессов, для которых значение энергии Гиббса понижается. Для изолированной системы DН = 0, следовательно, DG = –TDS 0
Изменение энергии Гиббса в процессе химической реакции находится по аналогии с правилом Гесса:
Изменение энергии Гиббса связано с константой равновесия реакции следующим уравнением: DG = –RTlnK
При вычислении стандартных изменений энтальпии, энтропии и энергии Гиббса обычно используют стандартные энтальпии и Энергии Гиббса образования простых веществ, которые является справочными величинами. Энтальпия образования и энергия Гиббса образования наиболее устойчивых простых веществ равны нулю.
Лекция 9.
Растворы.
Раствор – это гомогенная система переменного состава, состоящая из двух или более компонентов и продуктов их взаимодействия. Компоненты раствора – растворитель и растворенные вещества.
Вообще все дисперсные системы делятся на три группы: грубодисперсные (с диаметром частиц большим, чем 300 нм), коллоидные растворы (диаметр частиц от 1 до 300 нм) и истинные растворы (диаметр частиц меньше 1 нм).
Так как растворы в данном конкретном объеме не обладают постоянным составом, возникло понятие концентрации раствора – это содержание растворенного вещества в единице массы или объема растворителя или раствора. Существует много способов выражения концентрации раствора.
1. Для выражения концентрации по массе используют массовую долю – это массовая доля вещества в 100 г раствора, выражается в %:
2. Моляльная концентрация – число молей растворенного вещества в 1 кг растворителя, выражается в моль/кг:
3. Мольная доля раствора – количество данного вещества по отношению к количеству всех веществ, образующих раствор, безразмерная величина:
4. Молярная концентрация – количество вещества в 1 л раствора, выражается в моль/л:
5. Нормальная концентрация – число эквивалентных масс растворенного вещества в 1 л раствора:
Способность вещества переходить в раствор называется растворимостью вещества. Мера растворимости – концентрация вещества, достигаемая в насыщенном растворе.
Растворимость выражается двумя величинами: к – коэффициент растворимости – количество граммов вещества, растворяющегося в 100 г растворителя. К > 10 – малорастворимые; 10 > к > 1 – умеренно растворимые; 1 > к > 0,01 – малорастворимые; к
Количественно зависимость изменения температур замерзания и кипения от концентрации растворенного вещества выражает 2 закон Рауля: понижение температуры замерзания и повышение температуры кипения раствора прямо пропорционально моляльной концентрации растворенного вещества.
3. Осмос – односторонняя диффузия через полунепроницаемую мембрану. Сила, обуславливающая осмос, называется осмотическим давлением. По закону Вант-Гоффа осмотическое давление раствора равно тому газовому давлению, которое производило бы растворенное вещество, находясь в газообразном состоянии и занимая объем, равный объему раствора: Росм = СRT.
Растворы электролитов сильно отклоняются от законов Рауля и Вант-Гоффа. Поэтому Вант-Гофф предложил ввести изотонический коэффициент i для объяснения этих отклонений.
Лекция 10.
Растворы электролитов.
Поскольку осмотическое давление зависит от числа частиц растворенного вещества, находящихся в единице объема раствора, то шведский ученый Аррениус в 1887 году предположил, что некоторые вещества распадаются в растворе на ионы, что вызывает увеличение числа частиц в растворе.
Для объяснения свойств электролитов Аррениус предложил теорию электролитической диссоциации. Согласно данной теории вещества делятся на две группы: 1) вещества с ионной связью – в узлах кристаллической решетки уже ионы и в растворе разрушается кристаллическая решетка; 2) вещества с полярной ковалентной связью – под действием растворителя происходит ионизация молекул таких веществ.
Для характеристики свойств электролитов используют следующие понятия: степень ионизации и константа ионизации. Степенью ионизации называется отношение распавшихся на ионы формульных единиц вещества к их общему числу в растворе:
На степень ионизации влияет ряд факторов:
Константа ионизации представляет собой константу равновесия процесса ионизации электролита:
Константа ионизации связана со степенью ионизации законом разбавления Оствальда.
Данное уравнение показывает связь между концентрацией электролита и степенью его диссоциации: степень диссоциации возрастает при разбавлении раствора. Процесс диссоциации – процесс равновесный, при разбавлении равновесие сдвигается в сторону образования ионов. И, наоборот, при увеличении концентрации степень диссоциации падает. И даже для сильных электролитов реальная (кажущаяся) степень диссоциации меньше единицы и с увеличением концентрации снижается.
Для оценки действительной степени диссоциации ионов пользуются не концентрацией, а активностью: a = f×C, где f – коэффициент активности.
Коэффициент активности зависит от концентраций ионов, присутствующих в растворе, а точнее, от ионной силы раствора:
Согласно современным представлениям, кислотой является донор протона, то есть частица, способная отдавать протон, а основанием – акцептор протона, то есть частица, способная присоединять протон. Соотношение между кислотой и основанием определяется схемой:
Основание + Протон = Кислота
Связанные данным соотношение кислота и основание называются сопряженными. В зависимости от условий любая кислота может выступать также и в роли основания при реакции с более сильной кислотой.
Чистая вода ослабляет электрический ток в 81 раз, но все же обладает определенной электропроводностью, которая объясняется диссоциацией воды на катионы водорода и гидроксид-анионы:
Процесс диссоциации процесс равновесный, поэтому смещение равновесия процесса диссоциации подчиняется принципу Ле Шателье. Поэтому можно сделать следующий вывод. Обязательным условием завершенности реакции между электролитами является удаление из раствора каких-либо ионов вследствие образования слабодиссоциирующих веществ (слабых электролитов) или веществ, выделяющихся из раствора в виде газа или осадка. Образование таких веществ сдвигает равновесие в сторону образования продуктов реакции.
Энтропия. Ее изменение в химических процессах
Содержание:
| Предмет: | Химия |
| Тип работы: | Курсовая работа |
| Язык: | Русский |
| Дата добавления: | 15.05.2019 |
Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!
По этой ссылке вы сможете найти много готовых курсовых работ по химии:
Посмотрите похожие темы возможно они вам могут быть полезны:
Введение:
Предмет и задачи физической химии. Методы исследования в физической химии: термодинамические, статистические, квантово-механические, кинетические. Физическая химия изучает различные свойства веществ, их зависимость от химического состава, структуры, внешних условий, а также процессы, протекающие в веществах, условия и направления этих процессов.
В курсе физической химии обычно выделяют следующие разделы.
Структура вещества. Этот раздел включает в себя учение о строении атомов и молекул, учение о совокупных состояниях вещества. Изучение структуры вещества необходимо для выяснения наиболее важных вопросов о природе химических связей, а также о структуре и взаимодействии молекул и атомов. Этот раздел также включает кристаллохимию, зонную теорию строения твердого тела.
Химическая термодинамика. Объектом исследования являются энергетические эффекты, сопровождающие химические процессы, определение с их помощью возможности, направления и глубины химического процесса в определенных условиях.
Химическая кинетика. Он изучает скорость и механизм химических процессов в различных средах в различных условиях.
Учение о решениях Объектом исследования являются решения, процессы их формирования, внутренняя структура и важнейшие свойства, зависимость свойств от природы компонентов раствора.
Электрохимия изучает особенности свойств растворов электролитов, явления электропроводности, электролиза, коррозии, работы гальванических элементов.
Коллоидная химия. Объектом исследования являются поверхностные явления и свойства мелкодисперсных гетерогенных систем.
Для изучения различных процессов и свойств в физической химии используется ряд теоретических методов:
Химическая термодинамика
Основы химической термодинамики. Первый закон термодинамики
Термодинамика основана только на экспериментально открытых объективных законах.
Предмет изучения термодинамики:
Основные понятия, используемые в термодинамике.
Состояние любой термодинамической системы можно количественно охарактеризовать с помощью термодинамических переменных.
Переменные, которые фиксируются условиями существования системы и поэтому не могут изменяться в рамках рассматриваемой задачи, называются термодинамическими параметрами:
Любое изменение термодинамического состояния системы (изменение хотя бы одного параметра состояния) является термодинамическим процессом.
Одной из основных характеристик обеих систем и процессов, происходящих в них, является энергия.
Обычно в химической термодинамике рассматриваются стационарные системы в отсутствие внешних полей.
Первый закон (первый закон) термодинамики также называется законом сохранения энергии.
Существует аддитивная функция состояния термодинамической системы, называемая энергией (U). Энергия изолированной системы постоянна. В замкнутой системе энергия может быть изменена путем выполнения работы A над окружающей средой (или средой в системе) и обмена теплом Q с окружающей средой.
В системе СИ измерение работы, тепла и энергии составляет [Дж].
Позитивная работа идеально подходит в системе.
Тепло эквивалентно работе (установлено экспериментально).
Первый закон действителен для любых систем и процессов, но в случае открытых систем его нельзя использовать в виде уравнения dU = dQ + dA, поскольку в процессах, сопровождающихся переносом вещества из системы в окружающую среду или наоборот, наблюдаемые изменения энергии нельзя разделить на тепло и работу. Иногда для открытых систем первый закон записывается так: dU = dQ + dA +? mdni где? MDNI характеризует процесс обмена веществ между системой и окружающей средой. Эта сумма условно называется «химическая обработка», относящаяся к работе по переносу вещества из окружающей среды в систему. Функция m называется «химический потенциал». Внутренняя энергия является функцией состояния; это означает, что изменение внутренней энергии DU не зависит от перехода системы из состояния 1 в состояние 2 и равно разнице значений внутренней энергии U2 и U1 в этих состояниях:
Энтропия и ее изменение в химических реакциях
Чтобы определить, протекает ли химическая реакция спонтанно, необходимо знать движущие силы спонтанных процессов.
Одной из движущих сил химической реакции является уменьшение энтальпии системы, то есть экзотермический тепловой эффект реакции. Опыт показывает, что большинство спонтанных процессов являются экзотермическими, то есть сопровождаются выделением тепла (ΔH 0, то есть эндотермические, которые, тем не менее, происходят самопроизвольно, например, растворение некоторых солей (KCl, NH4Cl и т. д.) в воде.
Следовательно, существует другая движущая сила спонтанных процессов, не связанная с энтальпией. Это стремление частиц (молекул, ионов, атомов) к хаотическому движению, а систем к переходу из более упорядоченного состояния в менее упорядоченное.
Тенденция к беспорядку характеризуется количеством, названным энтропией. Таким образом, энтропия является термодинамической функцией, которая является мерой беспорядка в системе.
В качестве примера рассмотрим систему из двух газов, которые не реагируют друг с другом, например, аргон и гелий, которые разделены перегородкой и имеют одинаковую температуру и давление.
Мы удаляем раздел без изменения энергоснабжения системы. Мы называем это (начальное) состояние состояния системы 1.
Несмотря на одинаковое давление газа, процесс смешивания начнется, и через некоторое время молекулы гелия и аргона будут равномерно распределены по всей системе. Новое (конечное) состояние системы называется состоянием 2.
Опыт и теоретические расчеты показывают, что два газа, которые не разделены перегородкой, всегда смешиваются, вероятность состояния 1 незначительна. Состояние 2 равномерного распределения обоих газов наиболее вероятно. Аналогично, когда сахар растворяется в воде, наиболее вероятно будет состояние равномерного распределения молекул сахара в воде, а наименее вероятным будет исходное состояние (отдельно сахар, отдельно вода). Движущей силой смешения газов или растворения сахара является тенденция к переходу в наиболее вероятное состояние.
Это соотношение называется формулой Больцмана. Формула Больцмана позволяет теоретически рассчитать энтропию системы по числу ее возможных микросостояний. Такие расчеты хорошо согласуются с экспериментально определенными значениями.
Как и все термодинамические функции, энтропия является аддитивной функцией, то есть ее значение пропорционально размеру системы (масса, объем). Общепринятый размер энтропии: Дж / моль · К.
Энтропия вещества в стандартном состоянии называется стандартной энтропией S0 и приведена в справочниках.
В отличие от других термодинамических функций, можно определить не только изменение, но и абсолютное значение энтропии. Это следует из постулата, высказанного Максом Планком в 1911 году, согласно которому:
В абсолютном нуле энтропия идеального кристалла равна нулю.
Этот постулат называется третьим законом термодинамики.
Количество микросостояний кристаллических веществ при температуре 0 К мало. W0 ≈ 1. Подставляя это значение в выражение S = k · lnW, получаем S0 = 0.
При повышении температуры скорость различных типов движений частиц увеличивается, то есть число их микросостояний. Соответственно, термодинамическая вероятность и энтропия вещества увеличиваются. При переходе вещества из твердого состояния в жидкое состояние беспорядок значительно возрастает, а энтропия (ΔSPL) увеличивается. Особенно резко возрастает энтропия вещества при его переходе из жидкого в газообразное состояние (ΔSKIP). Так, для воды: S0KR = 45,99, S0 † = 70,08 и S0GAZ = 188,7 Дж / моль · К.
Из-за высоких значений энтропии газов последние называют «носителями энтропии». «»
Энтропия простых веществ является периодической функцией порядкового номера элемента. Увеличение числа атомов в молекуле приводит к увеличению энтропии. Например: S0 (O) = 161, S0 (O2) = 205 и S0 (O3) = 298,8 Дж / моль.
Изменение энтропии во время химической реакции может быть оценено без расчета, если объем газов изменяется во время реакции.
Например:
Однако реальные системы, в которых происходят химические реакции, не являются изолированными, поскольку они всегда обмениваются энергией (или энергией и веществом) с окружающей средой. Для этих систем, то есть закрытых или открытых, ни изменение энтропии, ни изменение энтальпии в отдельности не могут служить критерием для спонтанного процесса.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.