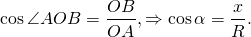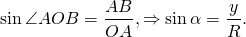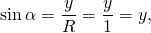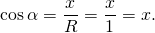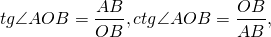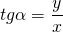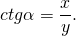Что называют единичной окружностью

Единичная окружность

Что такое единичная окружность и как с ее помощью вводятся определения синуса, косинуса, тангенса и котангенса?

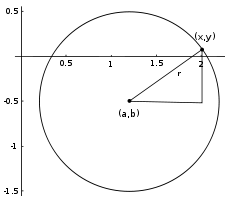
Рассмотрим в прямоугольной декартовой системе координат окружность с центром в начале координат — точке O.

Отметим на окружности точку P, лежащую на оси абсцисс справа от точки O.

Осуществим поворот радиуса OP около точки O на угол α в верхнюю полуплоскость.

При этом радиус OP займет положение OA. Говорят, что при повороте на угол альфа радиус OP переходит в радиус OA, а точка P переходит в точку точку A(x;y).

Опустив перпендикуляр AB из точки A на ось Оx, получим прямоугольный треугольник OAB, в котором гипотенуза OA равна радиусу окружности, катеты AB и OB — ординате и абсциссе точки A: OA=R, AB=y, OB=x.

Катет AB — противолежащий углу AOB, равному α, катет OB — прилежащий.

По определению косинуса острого угла в прямоугольном треугольнике,

Таким образом, на окружности косинус угла α — это отношение абсциссы точки A окружности к радиусу этой окружности.

Аналогично, по определению синуса острого угла в прямоугольном треугольнике,

Значит, синус угла α — это отношение ординаты точки A окружности к радиусу этой окружности.

Для окружности любого радиуса отношения x/R и y/R не зависят от величины радиуса, а зависят только от угла альфа. Поэтому удобно взять R=1. Для окружности единичного радиуса определение синуса и косинуса упрощаются:

Окружность с центром в начале координат и радиусом, равным единице, называется единичной окружностью.

Отсюда получаем определения синуса и косинуса на единичной окружности.

Синусом угла α называется ордината точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Косинусом угла α называется абсцисса точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Применив определения тангенса и котангенса острого угла в прямоугольном треугольнике в ∆AOB, получаем:

Приходим к определению тангенса и котангенса на единичной окружности.

Тангенсом угла α называется отношение ординаты точки A единичной окружности к абсциссе этой точки.

Котангенсом угла α называется отношение абсциссы точки A единичной окружности к ординате этой точки.

One Comment

Искала везде. Нигде нет такого подробного и понятного объяснения. Огромное Вам спасибо!

Источник

Окружность

Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом.

Содержание

Другие определения

Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. (см. Окружность Аполлония)

Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.

Связанные определения

Свойства

Основные формулы

Площадь круга радиуса R:

Площадь сектора, ограниченного углом α, измеряемым в градусах, радиусом R:

Площадь сегмента, ограниченного дугой окружности углом α, хордой:

Уравнения

Декартовы координаты

Общее уравнение окружности записывается как:

Точка — центр окружности, — её радиус.

Уравнение окружности радиуса с центром в начале координат:

Уравнение окружности, проходящей через три точки (с помощью определителя) и

Окружность также можно описать с помощью параметрического уравнения:

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

Если центр окружности совпадает с началом координат, функции принимают вид:

Полярные координаты

Окружность радиуса с центром в точке :

Если полярные координаты центра окружности то проходящая через начало координат окружность описывается уравнением:

Если же центр является началом координат, то уравнение будет иметь вид:

Комплексная плоскость

На комплексной плоскости окружность задаётся формулой:

или в параметрическом виде

Касательные и нормали

Уравнение касательной к окружности в точке определяется уравнением

Уравнение нормали в той же точке можно записать как

Концентрические и ортогональные окружности

Две окружности, заданные уравнениями:

являются концентрическими (то есть имеющими общий центр) в том и только в том случае, когда и

Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие

См. также

Литература

Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)

Конические сечения
Главные типы	Эллипс • Гипербола • Парабола
Вырожденные	Точка • Прямая • Пара прямых
Частный случай эллипса	Окружность
Геометрическое построение	Коническое сечение • Шары Данделена
См. также	Коническая константа
Математика • Геометрия

Полезное

Смотреть что такое «Окружность» в других словарях:

окружность — кольцо, эпицикл, кривая, местность, околоток, окрестность, деферент, круг, округа Словарь русских синонимов. окружность 1. см. круг. 2. см. окрестность … Словарь синонимов

ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра). Отрезок R, соединяющий центр окружности с какой либо её точкой (а также длина этого отрезка), называется радиусом; отрезок, соединяющий две точки… … Современная энциклопедия

ОКРУЖНОСТЬ — замкнутая плоская кривая, все точки которой одинаково удалены от ее центра O. (рис.). Расстояние R каждой точки окружности до ее центра называется радиусом. Прямая АВ, соединяющая любые две точки окружности, называется ее хордой, хорда CD,… … Большой Энциклопедический словарь

ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, расстояние, измеряемое по краю плоской геометрической фигуры, именуемой кругом, для которого это расстояние определяется как 2pr, где r радиус. Изредка этот термин применяют также к другим фигурам … Научно-технический энциклопедический словарь

ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, окружности, жен. 1. Замкнутая кривая, все точки которой равно удалены от точки, называемой центром; замкнутая кривая, ограничивающая плоскость круга (мат.). 2. Линия измерения кругообразных поверхностей и предметов. Яма метров десяти… … Толковый словарь Ушакова

ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, и, жен. 1. В математике: замкнутая на плоскости кривая, все точки к рой равно удалены от центра. 2. Линия измерения округлых, кругообразных поверхностей и предметов. О. водоёма. Воронка пяти метров в окружности. 3. Окружающая… … Толковый словарь Ожегова

Окружность — кривая линия, все точки которой находятся на одинаковомрасстоянии от одной внутренней точки, называемой центром. Прямые,проведенный из центра к точкам О., называются paдиуcaми. Прямая,проходящая чрез две точки О. и ограниченная этими точками,… … Энциклопедия Брокгауза и Ефрона

окружность — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN round … Справочник технического переводчика

ОКРУЖНОСТЬ — замкнутая плоская кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки О, лежащей в плоскости этой кривой и называемой её центром. Расстояние от любой точки окружности до её центра измеряется отрезком, называемым… … Большая политехническая энциклопедия

окружность — и; ж. 1. Матем. Замкнутая на плоскости кривая, все точки которой равно удалены от центра. 2. Линия измерения округлых, кругообразных поверхностей и предметов. О. озера. Воронка трёх метров в окружности. 3. Устар. Окружающая местность, округа. ◁ В … Энциклопедический словарь

Источник

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть

Источник

Синус, косинус

До сих пор мы измеряли углы только в градусах. Оказывается, есть и другая система измерения углов – радианы.

По определению, 1 радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу. Вот он, на рисунке.

Вспомним, что полный круг – это 360 градусов. Длина окружности равна 2πr. Составим пропорцию. Длина окружности так относится к длине дуги на нашем рисунке, как 360°- к величине угла, опирающегося на дугу на рисунке, то есть к углу в 1 радиан.

Слева в нашей пропорции углы, справа – длина полного круга и длина дуги на нашем рисунке.

Из этой пропорции получаем, что 360° = 2π радиан. Значит, полный круг – это 2π радиан. Тогда полкруга – это π радиан, четверть круга (то есть 90°) – это π/2 радиан.

Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот,

Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот, 1 радиан приблизительно равен 57 градусов.

Нарисуем единичную окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями OX и OY, в которой мы привыкли рисовать графики функций.

Договоримся отсчитывать углы от положительного направления оси ОХ против часовой стрелки.

Мы помним, что полный круг — это 360 градусов. Тогда точка с координатами (1;0) соответствует углу в 0 градусов. Точка с координатами (-1; 0) отвечает углу в 180 градусов, точка с координатами (0;1) — углу в 90 градусов. Каждому углу от нуля до 360 градусов соответствует точка на единичной окружности. Обратите внимание,что на нашем тригонометрическом круге углы отмечены и в градусах, и в радианах.

Источник

Единичный круг

Единичный круг — круг радиуса 1 на евклидовой плоскости (рассматриваемый обычно на комплексной плоскости); «идиоматическая» область в комплексном анализе.

Содержание

Определение

Единичный круг — открытое подмножество комплексной плоскости, задаваемое неравенством

или (что то же самое), .

В действительных координатах неравенство выглядит как:

.

Единичный круг обычно обозначается как или .

Автоморфизмы единичного круга

С точки зрения конформных отображений, автоморфизмы единичного круга составляют 3-мерную группу Ли, состоящую из дробно-линейных отображений специального вида:

Две степени свободы b обеспечиваются возможностью отобразить 0 (центр) в произвольную точку круга, а одна () — поворотами.

С точки зрения евклидовой геометрии, разумеется, кроме поворотов у круга автоморфизмов (движений) нет.

Модель Пуанкаре

Оказывается, что конформные автоморфизмы круга можно рассматривать и как метрические, но если рассмотреть на круге особую (неевклидову) метрику — метрику Пуанкаре:

Круг оказывается, таким образом, моделью плоскости Лобачевского.

Круг или полуплоскость?

С точки зрения комплексного анализа, в принципе, нет разницы, которую из односвязных областей на плоскости рассматривать — по теореме Римана они все эквивалентны (кроме самой плоскости). Чаще всего используют единичный круг и верхнюю полуплоскость. И единичный круг, и полуплоскость можно рассматривать как половинки сферы Римана, разрезанной большой окружностью.

Однако, для исследований связанных со степенными рядами удобнее рассматривать именно круги (см. круг сходимости).

Другие значения

В принципе, «единичным кругом» можно назвать круг единичного радиуса с центром не обязательно в нуле (начале координат), и не на евклидовой плоскости.

Полезное

Смотреть что такое «Единичный круг» в других словарях:

Круг (фигура) — Круг, основное значение часть плоскости, ограниченная окружностью. В переносном значении может употребляется для обозначения цикличности. Круг также является распространённой фамилией. Содержание 1 Термин 2 Фамилия 3 Прочие зна … Википедия

Единичный куб — Единичный куб это куб, длина ребра которого равна 1. Иногда требуют также чтобы одна вершина находилась в начале координат и все рёбра были параллельны осям системы координат. Объем единичного куба 1, площадь поверхности 6. Unit … Википедия

Единичный квадрат — квадрат в прямоугольных координатах, левый нижний угол которого находится в начале координат и имеет длины сторон по единице. The unit square in the real plane. Значит, его вершины имеют координаты … Википедия

Круг — У этого термина существуют и другие значения, см. Круг (значения). Круг Круг геометрическое место точек плоскос … Википедия

Тригонометрический круг — построенная на плоскости с прямоугольными декартовыми координатами окружность, имеющая центр в точке начала координат и единичный радиус, т.е. единичная окружность, которая используется для геометрического определения тригонометрических функций.… … Википедия

РИМАНОВА ПОВЕРХНОСТЬ — а н а л и т и ч е с к ой ф у н к ц и и w=f(z) к о м п л е к с н о г о п е р ем е н н о г о z поверхность R такая, что данная полная аналитическая функция w=f(z), вообще говоря многозначная, может рассматриваться как однозначная аналитич. ция… … Математическая энциклопедия

КОНФОРМНОЕ ОТОБРАЖЕНИЕ — непрерывное отображение, сохраняющее форму бесконечно малых фигур. Основные понятия. Непрерывное отображение w=f(z)области G n мерного евклидова пространства в n мерное евклидово пространство наз. конформным в точке если оно в этой точке обладает … Математическая энциклопедия

РИМАНОВЫХ ПОВЕРХНОСТЕЙ КЛАССИФИКАЦИЯ — изучение римановых поверхностей (р. п.), связанное с рассмотрением поведения функций различных классов на этих поверхностях. Комплексная функция на р. п. Rназ. а н а л и т и ч е с к о й на R, если для любой точки существуют окрестность Uи… … Математическая энциклопедия

Преобразование Мёбиуса — Вид преобразований на комплексной плоскости (серая) и сфере Римана (чёрная) Не следует путать с обращением Мёбиуса. Преобразование Мёбиуса дробно линейная функция одного комплексного переменного, тождественно не равная константе … Википедия

Группа Мёбиуса — Вид преобразований на комплексной плоскости (серая) и сфере Римана (чёрная) Содержание 1 Определение 2 Алгебраические свойства … Википедия

Источник