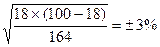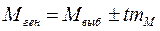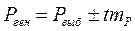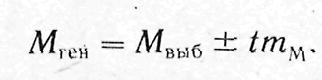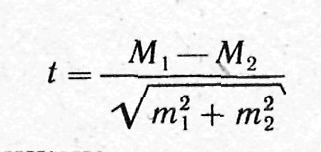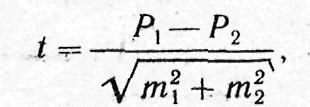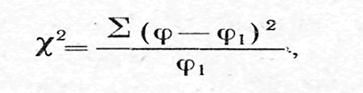Что называют доверительными границами средних и или относительных величин
Определение доверительных границ средних и относительных величин.
Формулы определения доверительных границ представлены следующим образом:
· для средних величин (М): Мген=Мвыб ± tm
· для относительных показателей (Р): Рген=Рвыб ± tm
Мвыб и Рвыб – значения средней величины и относительного показателя выборочной совокупности;
m- ошибка репрезентативности;
t— критерий достоверности (доверительный коэффициент).
Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности.
Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов, полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р), показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в генеральной совокупности.
При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам задает определенную (необходимую) степень вероятности безошибочного прогноза (Р).
Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t, зависящее также и от числа наблюдений.
ТогдаМген=Мвыб± tm =80±2х1=80±2 удара в мин.
Вывод: установлено с вероятностью безошибочного прогноза Р= 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 час работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген)
Условие задачи: при медицинском осмотре 164 детей 3-х летнего возраста, проживающих в одном из районов г. Н, в 18% случаев обнаружено нарушение осанки функционального характера.
Задание: определить ошибку репрезентативности (mР) и доверительные границы относительного показателя генеральной совокупности (Р ген).
Вычисление ошибки репрезентативности относительного показателя:
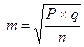
2. Вычисление доверительных границ средней величины генеральной совокупности (Рген): производится следующим образом:
а) необходимо задать степень вероятности безошибочного прогноза (Р =95%).
б) при заданной степени вероятности и числе наблюдений больше 30, величина критерия tравна2 (t=2).
ТогдаРген=Рвыб± tm =18%±2х3 = 18%±6%.
Вывод: установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3-х летнего возраста, проживающих в г. Н., будет находиться в пределах от 12% до 24% случаев.
Определение доверительных границ генеральной совокупности.



Определяя для средней арифметической (или относительной) величины два крайних значения: минимально возможное и максимально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами.
Доверительные границы — это то максимальное и минимальное значение, в пределах которого, при заданной степени вероятности безошибочного прогноза, может колебаться искомая средняя величина генерального параметра.
Доверительные границы средней арифметической в генеральной совокупности определяют по формуле:
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:
где Мген и Pген — значения средней и относительной величин, полученных для генеральной совокупности; Мвыб и Рвыб —значения средней и относительной величин, полученных для выборочной совокупности; mM и mР — ошибки репрезентативности выборочных величин; t — доверительный критерий (критерий точности, который устанавливают при планировании исследования; tm — доверительный интервал; tm=Δ, где Δ предельная ошибка показателя, полученного при выборочном исследовании.
Размеры предельной ошибки (Δ) зависят от коэффициента t, который избирает сам исследователь, исходя из необходимости получить результат с определенной степенью точности.
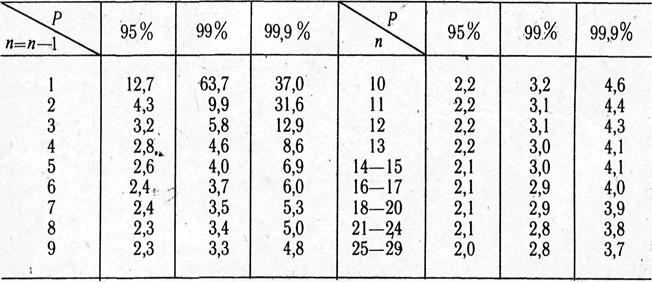
Величина критерия t связана определенными отношениями с вероятностью безошибочного прогноза — р и численностью наблюдений в выборочной совокупности.
Зависимость доверительного критерия t от степени вероятности
безошибочного прогноза (при n>30)
| Степень вероятности безошибочного прогноза в % | Доверительный критерий —t |
| 95,0 | |
| 99,0 |
Для большинства медико-биологических и социальных исследований достоверными считаются доверительные границы, установленные с вероятностью безошибочного прогноза р = 95% и более. Чтобы найти критерий t при числе наблюдений n
Любой параметр (средняя величина или относительная величина) может оцениваться с учетом доверительных границ, полученных при расчете.
Для ознакомления с методикой определения доверительных границ Мвыб и Рвыб рекомендуется записать исходные данные и провести расчеты в определенной логической последовательности:
Пример 1. Определить доверительные границы среднего уровня пепсина у больных гипертиреозом с 95% вероятностью безошибочного прогноза (р = 95%).
Условие задачи: n=49
р = 95% (следовательно при n = 49 t = 2).
Определяем доверительные границы средней величины в генеральной совокупности.
Решение : Мген = 1 г% ± 2 х 0,05 г%
Мген не более 1 г% +0,1 г% = 1,1 г%,
Мген не менее 1 г%—0,1 г% =0,9 г%.
Вывод: Установлено с вероятностью безошибочного прогноза (р = 95%>, что средний уровень пепсина в генеральной совокупности у больных с гипертиреозом не превышает 1,1 г% и не ниже 0,9 г%.
Пример 2. Определить доверительные границы показателя частоты дистрофии пародонта у больных с абсцессом легкого с вероятностью безошибочного прогноза р = 95%.
р =95% (следовательно, при n=110 t=2).
Определяем доверительные границы относительного показателя в генеральной совокупности.
Решение: Рген = 49% ±2 х 4,7%
Рген не более 40% + 9,4 = 49,4%
Рген не менее 40% –9,4 = 30,6%
Вывод: Установлено с 95% вероятностью безошибочного прогноза (р = 95%), что дистрофические изменения пародонта в генеральной совокупности наблюдаются у больных с абсцессом легкого не чаще, чем в 49,4%, и не реже, чем в 30,6% случаев.
Как видно, доверительные границы зависят от размера доверительного интервала (tm=Δ).
Анализ доверительных интервалов указывает, что при заданных степенях вероятности (р) и n ≥30 t имеет неизменную величину и при этом доверительный интервал зависит от величины ошибки репрезентативности (mм или mР).
С уменьшением величины ошибки суживаются доверительные границы средних и относительных величин, полученных на выборочной совокупности, т. е. уточняются результаты исследования, которые приближаются к соответствующим величинам генеральной совокупности.
Если ошибка большая, то получают для выборочной величины большие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности.
Например, при определенном режиме питания и тренировок спортсменов средняя годовая прибавка массы тела у 80 спортсменов составила Мвыб=1 кг; mM= ±0,8 кг. При степени вероятности р = 95,0% и t = 2 Мген = 1 кг ± 2 х 0,8 кг. Следовательно:
Мген не более + 2,6 кг,
Мген не менее – 0,6 кг.
Эти противоречивые данные означают, что при указанном режиме спортсмены могут дать большую среднюю прибавку массы тела (до +2,6 кг), но могут и убавить массу тела в среднем на 600 г. Таким образом, остается по-прежнему невыясненным вопрос о степени влияния данного режима спортсменов на массу их тела.
В подобном случае надо искать резервы сокращения размаха доверительных границ в размере величины ошибки репрезентативности. Прежде всего надо проанализировать уровень разнообразия признака по среднему квадратическому отклонению (σ) с позиций однородности группы. Необходимо также иметь в виду, что большое влияние на величину средней ошибки, а следовательно, и на доверительные границы оказывает численность наблюдений.
Доверительные границы Мвыб и Рвыб зависят не только от средних ошибок этих величин (mM или mР), но и от избранной исследователем степени вероятности безошибочного прогноза (р). При большой степени вероятности размах доверительных границ увеличивается.
Определение доверительных границ М и Р
Определяя для средней арифметической (или относительной) величины два крайних значения: минимально возможное и максимально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами.
Доверительные границы — границы средних (или относительных) величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность.
Доверительные границы средней арифметической в генеральной совокупности определяют по формуле:
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:
Размеры предельной ошибки (D) зависят от коэффициента t, который избирает сам исследователь, исходя из необходимости получить результат с определенной степенью точности.
Зависимость доверительного критерия / от степени вероятности безошибочного прогноза р (при n>30)
| Степень вероятности безошибочного прогноза – P, % | Доверительный критерий t |
| 95,0 % (0,05) 99,0 % (0,01) |
Для большинства медико-биологических и социальный исследований достоверными считаются доверительные границы, установленные с вероятностью безошибочного прогноза р = 95% и более. Чтобы найти критерий t при числе наблюдений п
При определении доверительных границ сначала надо решить вопрос о том, с какой степенью вероятности безошибочного прогноза необходимо представить доверительные границы средней или относительной величины. Избрав определенную степень вероятности, соответственно этому находят величину доверительного критерия t при данном числе наблюдений. Таким образом, доверительный критерий t устанавливается заранее, при планировании исследования.
Любой параметр (средняя величина или относительная величина) может оцениваться с учетом доверительных границ, полученных при расчете.
Как видно, доверительные границы зависят от размера доверительного интервала (tm= D).
С уменьшением величины ошибки суживаются доверительные границы средних и относительных величин, полученных на выборочной совокупности, т. е. уточняются результаты исследования, которые приближаются к соответствующим величинам генеральной совокупности.
Если ошибка большая, то получают для выборочной величины большие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности.
3. Определение достоверности разности средних (или относительных) величин (по критерию t). Критерий Стьюдента. В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т. д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность.
Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.
Формула оценки достоверности разности сравниваемых средних величин такова:
и для относительных величин:
Для большинства исследований, проводимых в биологии, такая степень вероятности является вполне достаточной.
При величине критерия достоверности t 2 соответствие эмпирического распределения теоретическому, оценивают достоверность различия между выборочными совокупностями.
Критерий c 2 (в отличие от критерия t) применяется в тех случаях, когда нет необходимости знать величину того или иного параметра (среднюю или относительный показатель) и требуется оценить достоверность различия не только двух, но и большего числа групп.
Так, критерий соответствия c 2 может быть использован для ответа на следующие вопросы: существенно ли отличаются друг от друга группы вакцинированных и невакцинированных по распределению их на больных и здоровых (т.е. эффективна ли вакцина); существенно ли отличаются группы населения с разным среднедушевым доходом по распределению их на больных и здоровых (т.е. влияет ли материальное обеспечение на уровень заболеваемости) и т. д.
Критерийc 2 (хи-квадрат) определяется по формуле:
Такой принцип доказательства «от противного» является довольно распространенным во многих исследованиях и применяется при расчете критерия c 2
Последовательность расчета критерия на примере.
Требуется оценить при помощи критерия c 2 различаются ли по срокам заболеваемости корью группа вакцинированных и невакцинированных лиц (до вакцинации и после вакцинации).
Этапы расчета представлены в табл.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ
Оценить достоверность результатов исследования означает определить, с какой вероятностью возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность.
Оценка достоверности результатов исследования предусматривает определение:
2) доверительных границ средних (или относительных) величин;
Определение средней ошибки средней (или относительной) величины (ошибка репрезентативности – т).
Теория выборочного метода, наряду с обеспечением репрезентативности, практически сводится к оценке расхождений между числовыми характеристиками генеральной и выборочной совокупности, т. е. к определению средних ошибок и так называемых доверительных границ или интервалов. Средняя ошибка позволяет установить тот интервал, в котором заключено действительное значение производной величины при данном числе наблюдений, т. е. средняя ошибка всегда является конкретной.
Ошибка репрезентативности является важнейшей статистической величиной, необходимой для оценки достоверности результатов исследования. Эта ошибка возникает в тех случаях, когда требуется по части охарактеризовать явление в целом. Эти ошибки неизбежны. Они «вытекают» из сущности выборочного исследования. Генеральная совокупность может быть охарактеризована по выборочной совокупности только с некоторой погрешностью, измеряемой ошибкой репрезентативности.
Ошибки репрезентативности не тождественны обычным представлением об ошибках: методических, точности измерения, арифметических и др.
По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном исследовании, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования без исключения всех элементов генеральной совокупности.
Это единственный вид ошибок, учитываемых статистическими методами, которые не могут быть устранены, если не проведено сплошное исследование.
Ошибки репрезентативности можно свести к достаточно малой величине, т.е. к величине допустимой погрешности. Делается это путем увеличения числа наблюдений (n).
Средняя арифметическая величина выборочной совокупности (М) имеет ошибку репрезентативности, которая называется средней ошибкой средней арифметической (mМ) и определяется по формуле:




На этом принципе основан метод определения достаточного числа наблюдений для выборочного исследования.
Относительные величины (Р), полученные при выборочном исследовании, также имеют свою ошибку репрезентативности, которая называется средней ошибкой относительной величины и обозначается mр.
Для определения средней ошибки относительной величины (Р) используется следующая формула:
 |

 |

Каждая средняя арифметическая или относительная величина, полученная на выборочной совокупности, должна быть представлена со своей средней ошибкой. Это дает возможность рассчитать доверительные границы средних и относительных величин, а также определить достоверность разности сравниваемых показателей (результатов исследования).
2. Определение доверительных границ.
Определяя для средней арифметической (или относительной) величины два крайних значения: минимально возможное и максимально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами.
Вероятность попадания средней или относительной величины в доверительный интервал называется доверительной вероятностью.
Доверительные границы средней арифметической генеральной совокупности определяют по формуле:
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:
Размеры предельной ошибки зависят от коэффициента t, который избирает сам исследователь, исходя из заданной вероятности безошибочного прогноза.
Величина критерия t связана с вероятностью безошибочного прогноза (Р) и числом наблюдений в выборочной совокупности (табл. 2.6).
Таблица 2.6
Зависимость доверительного критерия t от степени вероятности безошибочного прогноза Р (при n > 30)
| Степень вероятности безошибочного прогноза (Р %) | Доверительный критерий t |
| 95,0 | |
| 99,0 | 2,6 |
| 99,9 | 3,3 |
Для большинства медико-биологических и социальных исследований достоверными считаются доверительные границы, установленные с вероятностью безошибочного прогноза = 95% и более.
С уменьшением величины ошибки суживаются доверительные границы средних и относительных величин, полученных на выборочной совокупности, т.е. уточняются результаты исследования, которые приближаются к соответствующим величинам генеральной совокупности. Если ошибка большая, то получают для выборочной величины большие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности. В подобном случае надо искать резервы сокращения размаха доверительных границ в размере величины ошибки репрезентативности.
Доверительные границы Мвыб и Рвыб зависят не только от средних ошибок этих величин, но и от избранной исследователем степени вероятности безошибочного прогноза. При большой степени вероятности размах доверительных границ увеличивается.
В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т.д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность.
Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.
Достоверность разности выборочной совокупности измеряется доверительным критерием, который рассчитывается по специальным формулам для средних и относительных величин.
Формула оценки достоверности разности сравниваемых средних величин:


Для относительных величин:
 |
Где: M1; M2 ; Р1; Р2 — параметры, полученные при выборочных исследованиях;
Разность статистически достоверна при t ≥ 2, что соответствует вероятности безошибочного прогноза, равной 95% и более.
Для большинства исследований, проводимых в медицине и здравоохранении, такая степень вероятности является вполне достаточной.
При величине критерия достоверности t 99,9
 |
 |
Заключение: при гипертериозе наблюдается снижение уровня пепсина, что подтверждается с большой степенью вероятности безошибочного прогноза (Р > 99,9%). Следовательно, снижение уровня пепсина может быть использовано в качестве одного из симптомов для подтверждения диагностики гипертериоза.
Подобным же образом оценивают достоверность разности сравниваемых относительных величин.