Что называют длиной и шириной прямоугольника
ВОПРОСЫ
1. Какой четырехугольник называют прямоугольником?
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
2. Какие стороны прямоугольника называют соседними? Противолежащими?
3. Что называют длиной и шириной прямоугольника?
Соседние стороны прямоугольника, т.е. стороны имеющие общую вершину, называют его длиной и шириной.
4. Каким свойством обладают противолежащие стороны прямоугольника?
Противолежащие стороны прямоугольника равны.
5. Какую фигуру называют квадратом?
Квадратом называют прямоугольник, у которого все стороны равны.
6. Объясните, какие фигуры называют симметричными относительно прямой.
7. Как называют прямую, относительно которой симметрична фигура?
Прямую, относительно которой симметрична фигура, называют осью симметрии фигуры.
8. Какие вы знаете фигуры, имеющие ось симметрии?
Прямоугольник, квадрат, равнобедренный и равносторонний треугольники.
9. Сколько осей симметрии имеет прямоугольник, отличный от квадрата? Квадрат? Равносторонний треугольник?
РЕШАЕМ УСТНО
1. Каждая сторона треугольника равна 12 см. Как называют такой треугольник? Чему равен его периметр?
3. Найдите сторону равностороннего треугольника, если она меньше его периметра на 10 см.
4. Вычислите значение по формуле y= x*x+ 12, если: 1) x = 1; 2) x = 10.
УПРАЖНЕНИЯ
359. Постройте: 1) прямоугольник, соседние стороны которого равны 4 см и 2 см; 2) квадрат со стороной 3 см.
360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.
361. Вычислите периметр: 1) прямоугольника, соседние стороны которого равны 42 см и 23 см; 2) квадрата со стороной 8 дм.
362. Найдите периметр прямоугольника, соседние стороны которого равны 13 мм и 17 мм.
363. Какие из букв, изображенных на рисунке 135, имеют ось симметрии?
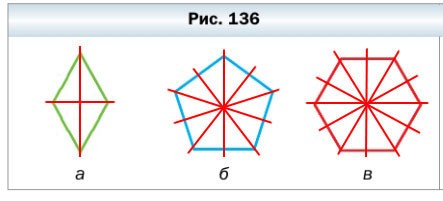
364. Сколько осей симметрии имеет многоугольник, изображенный на рисунке 136?
367. Квадрат со стороной 12 см и прямоугольник, одна из сторон которого равна 8 см, имеют равные периметры. Найдите неизвестную сторону прямоугольника.
368. Прямоугольник, соседние стороны которого равны 42 см и 14 см, и квадрат имеют равные периметры. Найдите длину стороны квадрата.
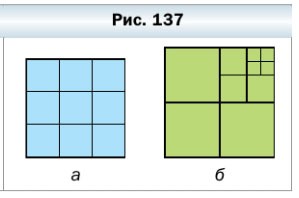
369. Сколько квадратов изображено на рисунке 137?
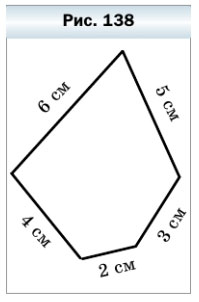
370. Из куска проволоки сделали модель пятиугольника (рис. 138). Какие из моделей перечисленных фигур, длины сторон которых выражаются натуральным числом сантиметров, можно сделать из этого куска проволоки: 1) квадрат; 2) пятиугольник, все стороны которого равны; 3) равносторонний треугольник?
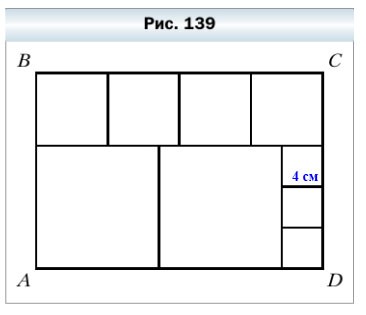
371. Прямоугольник АВCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника АВСD.
372. Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача?
373. Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.
374. Как надо разрезать квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?
375. Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?
376. Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?
377. Как надо разрезать квадрат на треугольник и четырехугольник, чтобы из них можно было сложить треугольник?
378. Как надо разрезать квадрат со стороной 6 см на две части по ломаной, состоящей из трех звеньев, чтобы из полученных частей можно было сложить прямоугольник?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
379. Проведите прямую МК, луч PS и отрезок АВ так, чтобы луч РS пересекал отрезок АВ и прямую МК, а прямая МК не пересекала отрезок АВ.
380. В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?
381. От дома до дачи можно доехать на автобусе, или на электропоезде, или на маршрутном такси. В таблице указано время, которое надо затратить на каждый участок пути. Какой наименьшее время потребуется на дорогу? Каким видом транспорта надо воспользоваться?
382. Найдите сумму корней уравнений:
ЗАДАЧА ОТ МУДРОЙ СОВЫ
383. Как с помощью пятилитрового бидона и трехлитровой банки набрать на берегу реки 4 л воды?
Мерзляк 5 класс — § 15. Прямоугольник. Ось симметрии фигуры
Вопросы к параграфу
1. Какой четырёхугольник называют прямоугольником?
Прямоугольник — это четырёхугольник, у которого все углы прямые.
2. Какие стороны прямоугольника называют соседними? Противолежащими?
3. Что называют длиной и шириной прямоугольника?
Длиной и шириной прямоугольника называют соседние стороны прямоугольника.
4. Каким свойством обладают противолежащие стороны прямоугольника?
Противолежащие стороны прямоугольника равны.
5. Какую фигуру называют квадратом?
Квадрат — это прямоугольник, у которого все стороны равны.
6. Объясните, какие фигуры называют симметричными относительно прямой.
Фигуру называют симметричной, относительно прямой, если при сгибе по этой прямой противоположные части фигуры совпадают друг с другом.
7. Как называют прямую, относительно которой симметрична фигура?
8. Какие вы знаете фигуры, имеющие ось симметрии?
Круг, равнобедренный и равносторонний треугольник, квадрат, прямоугольник.
9. Сколько осей симметрии имеет прямоугольник, отличный от квадрата? Квадрат? Равносторонний треугольник?
Решаем устно
1. Каждая сторона треугольника равна 12 см. Как называют такой треугольник? Чему равен его периметр?
Такой треугольник называют равносторонним. Его периметр равен P = 3a = 3 • 12 = 36 см.
Ответ: равносторонний, 36 см.
2. Периметр равнобедренного треугольника равен 32 см, а одна из его сторон — 12 см. Найдите длины двух других сторон треугольника. Сколько решений имеет задача?
Задача может иметь 2 решения.
Решение 1.
Пусть 12 см — это длина основания равнобедренного треугольника. Тогда, при периметре 32 см, боковые стороны этого треугольника будут равны:
(32 — 12) : 2 = 20 : 2 = 10 (см) — длина каждой из боковых сторон треугольника.
Ответ: двумя другими сторонами будут две боковые стороны: 10 см и 10 см.
Решение 2:
Пусть 12 см — это длина одной из боковых сторон равнобедренного треугольника. Тогда вторая боковая сторона этого треугольника также равна 12 см, а основание, при периметре треугольника 32 см, будет равно:
32 — 12 • 2 = 32 — 24 = 8 (см) — длина основания треугольника.
Ответ: двумя другими сторонами будут: основание — 8 см и вторая боковая сторона — 12 см.
3. Найдите сторону равностороннего треугольника, если она меньше его периметра на 10 см.
У равностороннего треугольника все три стороны равны, а периметр — это сумма все сторон треугольника.
Если одна сторона равностороннего треугольника меньше периметра на 10 см, значит сумма двух оставшихся сторон равна 10 см.
10 : 2 = 5 (см) — длина стороны равностороннего треугольника.
4. Вычислите значение у по формуле у = х • х + 12, если:
у = 1 • 1 + 12 = 1 + 12 = 13
у = 10 • 10 + 12 = 100 + 12 = 112
Упражнения
359. Постройте:
1) прямоугольник, соседние стороны которого равны 4 см и 2 см
2) квадрат со стороной 3 см
AB = BC = CD = DA = 3 см
360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.
361. Вычислите периметр:
1) прямоугольника, соседние стороны которого равны 42 см и 23 см
P = 2a + 2b = 2 • 42 + 2 • 23 = 84 + 46 = 130 (см)
2) квадрата со стороной 8 дм
P = 4a = 4 • 8 = 32 (дм)
362. Найдите периметр прямоугольника, соседние стороны которого равны 13 мм и 17 мм.
P = 2a + 2b = 2 • 13 + 2 • 17 = 26 + 34 = 60 (мм)
363. Какие из букв, изображённых на рисунке 135, имеют ось симметрии?
Ось симметрии имеют в данном случае буквы А, В, Е, Т.
364. Сколько осей симметрии имеет многоугольник, изображённый на рисунке 136?
365. 1) Длина одной из сторон прямоугольника равна 14 см, что на 5 см больше длины соседней стороны. Найдите периметр прямоугольника.
1) 14 — 5 = 9 (см) — длина соседней стороны прямоугольника
2) 2 • 14 + 2 • 9 = 28 + 18 = 46 (см)
2) Периметр прямоугольника равен 34 см, а одна из его сторон — 12 см. Найдите длину соседней стороны прямоугольника.
1) 12 • 2 = 24 (см) — сумма длин двух противоположных сторон прямоугольника
2) 34 — 24 = 10 (см) — сумма длин двух других, соседних им, противоположных сторон треугольника.
3) 10 : 2 = 5 (см) — длина соседней стороны прямоугольника.
366. Одна сторона прямоугольника равна 8 см, а соседняя — в 4 раза больше. Найдите периметр прямоугольника.
1) 8 • 4 = 32 (см) — длина соседней стороны прямоугольника.
2) 2 • 8 + 2 • 32 = 16 + 64 = 80 (см)
367. Квадрат со стороной 12 см и прямоугольник, одна из сторон которого равна 8 см, имеют равные периметры. Найдите неизвестную сторону прямоугольника.
1) 12 • 4 = 48 (см) — периметр квадрата.
2) 8 • 2 = 16 (см) — сумма двух противоположных сторон прямоугольника.
3) 48 — 16 = 32 (см) — сумма длин двух других, соседних им, противоположных сторон треугольника.
4) 32 : 2 = 16 см (см) — длина соседней стороны прямоугольника.
368. Прямоугольник, соседние стороны которого равны 42 см и 14 см, и квадрат имеют равные периметры. Найдите длину стороны квадрата.
1) 2 • 42 + 2 • 14 = 84 + 28 = 112 (см) — периметр прямоугольника.
2) 112 : 4 = 28 (см) — длина стороны квадрата.
369. Сколько квадратов изображено на рисунке 137?
370. Из куска проволоки сделали модель пятиугольника (рис. 138).
Какие из моделей перечисленных фигур, длины сторон которых выражаются натуральным числом сантиметров, можно сделать из этого куска проволоки: 1) квадрат; 2) пятиугольник, все стороны которого равны; 3) равносторонний треугольник?
1) 5 + 3 + 2 + 4 + 6 = 20 (см) — проволоки потребовалось для изготовления первоначальной модели.
2) 20 : 4 = 5 (см) — длина стороны квадрата, сделанного из этого куска проволоки.
3) 20 : 5 = 4 (см) — длина стороны пятиугольника, сделанного из этого куска проволоки.
4) 20 : 3 ≠ натуральному числу. Значит из этого куска проволоки нельзя изготовить равносторонний треугольник, длины сторон которого выражаются натуральным числом.
Ответ: квадрат и пятиугольник.
371. Прямоугольник ABCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника ABCD.
1) 4 • 3 = 12 (см) — длина стороны большого квадрата.
2) AD = 12 + 12 + 2 = 24 + 4 = 28 (см) — длина нижней стороны прямоугольника ABCD.
3) AD = BC = 28 (см) — длина верхней стороны прямоугольника ABCD.
4) 28 : 4 = 7 (см) — длина стороны среднего квадрата.
5) AB = 12 + 7 = 19 (см) — длина боковой стороны прямоугольника ABCD
6) AB = CD = 19 (см) — длина противоположной боковой стороны прямоугольника ABCD
Ответ: у прямоугольника ABCD две стороны по 19 см и дву стороны по 28 см.
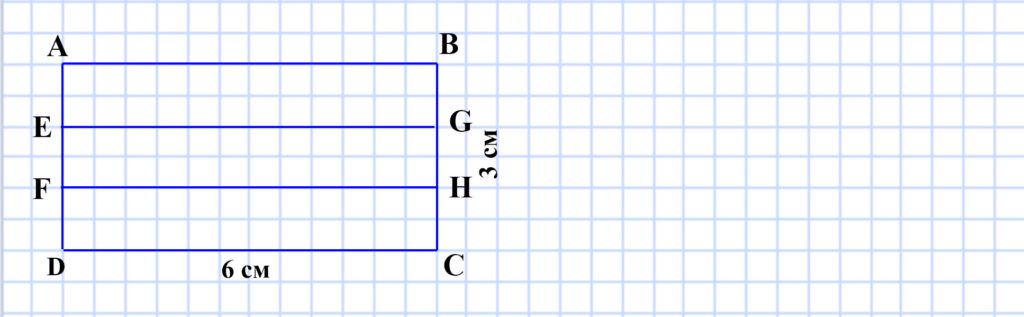
372. Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача?
Задача имеет 2 решения.
Решение 1.
a = AB = EG = FH = DC = 6 (см) — длина стороны малого прямоугольника.
b = AE = EF = FD = BG = GH = HC = 3 : 3 = 1 (см) — длина соседней стороны малого прямоугольника.
P = 2a + 2b = 2 • 6 + 2 • 1 = 12 + 2 = 14 (см) — периметр малого прямоугольника.
Решение 2.
a = AD = KM = LN = BC = 3 (см) — длина стороны малого прямоугольника.
b = AK = KL = LB = DM = MN = NC = 6 : 3 = 2 (см) — длина соседней стороны малого прямоугольника.
P = 2a + 2b = 2 • 3 + 2 • 2 = 6 + 4 = 10 (см) — периметр малого прямоугольника.
373. Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.
Да, такой прямоугольник существует. Например, прямоугольник ABCD со сторонами AB = DC= 4 см и AD = BC = 2 см. Его периметр P = 12 см (2 • 4 + 2 • 2 = 8 + 4 = 12) и его можно разделить на 2 равных квадрата со сторонами 2 см. Это квадраты AMLD и MBCL.
Вычислим периметр полученных квадратов (так как квадраты равные, то и их периметры тоже равны):
Ответ: Да, возможно. Периметр каждого из образованных квадратов AMLD и MBCL равен 8 см.
374. Как надо разрезать квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?
375. Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?
376. Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?
377. Как надо разрезать квадрат на треугольник и четырёхугольник, чтобы из них можно было сложить треугольник?
378. Как надо разрезать квадрат со стороной 6 см на две части по ломаной, состоящей из трёх звеньев, чтобы из полученных частей можно было сложить прямоугольник?
Упражнения для повторения
379. Проведите прямую МК, луч PS и отрезок АВ так, чтобы луч PS пересекал отрезок АВ и прямую МК, а прямая МК не пересекала отрезок АВ.
380. В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?
1) 740 — (55 + 36 + 34) = 740 — (55 + 70) = 740 — 125 = 615 (кг) — фруктов осталось в магазине после продажи.
2) 615 : 3 = 205 (кг) — масса каждого вида фруктов осталось в магазине.
3) 205 + 55 = 260 (кг) — лимонов было в магазине изначально.
4) 205 + 36 = 241 (кг) — апельсинов было в магазине изначально.
5) 205 + 34 = 239 (кг) — мандаринов было в магазине изначально.
Ответ: лимонов — 260 кг, апельсинов — 241 кг, мандаринов — 239 кг.
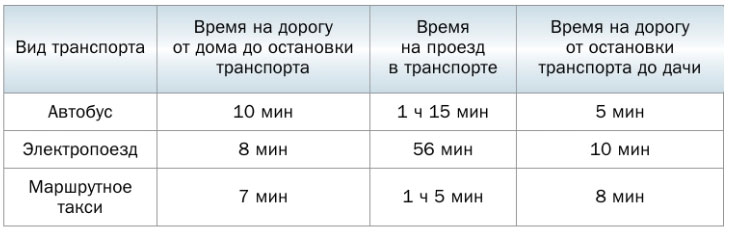
381. От дома до дачи можно доехать на автобусе, или на электропоезде, или на маршрутном такси. В таблице указано время, которое надо затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Каким видом транспорта при этом надо воспользоваться?
1) 10 мин + 1 ч 15 мин + 5 мин = 1 ч 30 мин — потребуется для поездки на автобусе.
2) 8 мин + 56 мин + 10 мин = 74 мин = 1 ч 14 мин — потребуется для поездки на электропоезде.
3) 7 мин + 1 ч 5 мин + 8 мин = 1 ч 20 мин — потребуется для поездки на маршрутном такси.
Ответ: наименьшее время на дорогу — 1 ч 14 мин, для этого надо воспользоваться электропоездом.
382. Найдите сумму корней уравнений:
Задача от мудрой совы
383. Как с помощью пятилитрового бидона и трёхлитровой банки набрать на берегу реки 4 л воды?
При последнем действии мы сможем вылить в банку только 1 литр воды, так как в ней уже есть 2 литра воды. То есть в 5-литровом бидоне останется искомые 4 литра воды (5 — 1 = 4).