Что называют диагональю многогранника

Что такое многогранник? Примеры

Примеры многогранников:

1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);

Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.

Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.

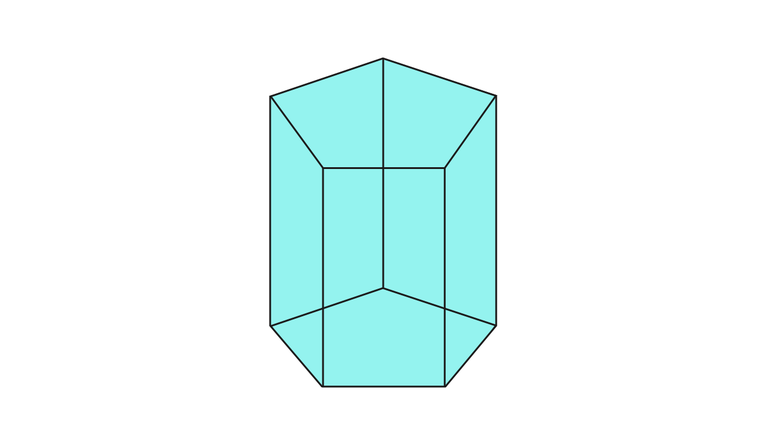
Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.

Популярное

Он круглый, но развёртку деталей для его сборки никто не отменял!

Нам нужны еще фонарики Джека в форме тыквы. Кто же нам поможет? Может быть Архимед?

Современный кинематограф постарался привлечь внимание зрителя, используя геометрические формы «инопланетного происхождения».

Архитектурные шедевры находятся в разных уголках земного шара и отражают особенности человеческой души. Тайные людские желания воплощаются в форме необыкновенных зданий. В.

Источник

math4school.ru

Многогранники

Основные понятия

Некоторые пространственные фигуры, изучаемые в стереометрии, называют телами или геометрическими телами. Наглядно тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.

Многогранником называется геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников.

Выпуклым называется многогранник, если он расположен по одну сторону плоскости, проведённой через любой многоугольник, образующий поверхность данного многогранника.

Многоугольники, составляющие поверхность многогранника, называются его гранями; стороны многоугольников – рёбрами; вершины – вершинами многогранника:

Теорема Эйлера для многогранников:

Если V — число вершин выпуклого многогранника, R — число его ребер и G — число граней, то верно равенство:

Призма

Призмой называется многогранник, состоящий из двух плоских многоугольников, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники, о которых шла речь, называются основаниями призмы, а отрезки, соединяющие их соответствующие вершины – боковыми рёбрами призмы.

Основания призмы равны и лежат в параллельных плоскостях.

Боковые рёбра призмы равны и параллельны.

Поверхность призмы состоит из двух оснований и боковой поверхности.

Боковая поверхность любой призмы состоит из параллелограммов, у каждого из которых две стороны являются соответствующими сторонами оснований, а две другие – соседними боковыми рёбрами.

Высотой призмы называется любой из перпендикуляров, проведённых из точки одного основания к плоскости другого основания призмы.

A₁О – высота призмы;

α – угол наклона бокового ребра к основанию призмы.

Призма называется прямой, если её рёбра перпендикулярны плоскостям оснований. В противном случае призма называется наклонной.

Боковые грани прямой призмы – прямоугольники.

Боковое ребро прямой призмы является её высотой.

Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы:

Прямая призма называется правильной, если её основания являются правильными многоугольниками.

Сечения призмы плоскостями, параллельными боковым рёбрам,являются параллелограммами. В частности, параллелограммами являются диагональные сечения. Это сечения плоскостями, проходящими, через два боковых ребра, не принадлежащих одной грани:

ВВ₁D₁ D – диагональное сечение.

Если в произвольной наклонной призме провести сечение, перпендикулярное боковым рёбрам и пересекающее все боковые рёбра, и площадь этого сечения обозначить S_⊥, а периметр – Р_⊥, тогда:

В любой призме площадь полной поверхности считается как сумма площади боковой поверхности и удвоенной площади основания:

Параллелепипед

Призма, в основании которой лежит параллелограмм, называется параллелепипедом.

У параллелепипеда все грани – параллелограммы.

Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.

У параллелепипеда противолежащие грани параллельны и равны.

Диагональю параллелепипеда, как и многогранника вообще, называется отрезок, соединяющий вершины параллелепипеда, не лежащие в одной его грани.

Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Точка пересечения диагоналей параллелепипеда является его центром симметрии.

Прямоугольным параллелепипедом называется такой прямой параллелепипед, в основании которого лежит прямоугольник.

Все грани прямоугольного параллелепипеда являются прямоугольниками.

Длины рёбер прямоугольного параллелепипеда, выходящих из одной вершины, называются его измерениями или линейными размерами.

У прямоугольного параллелепипеда три измерения.

В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений:

В прямоугольном параллелепипеде верно:

В прямоугольном параллелепипеде, как и во всяком параллелепипеде, есть центр симметрии – точка пересечения его диагоналей. У него есть также три плоскости симметрии, проходящие через центр симметрии параллельно парам противолежащих граней. На первом рисунке, приведённом выше, показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда.

Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме трёх названных.

Если же у параллелепипеда два линейных размера равны, то есть он является правильной четырёхугольной призмой, то у него есть еще две плоскости симметрии. Это плоскости диагональных сечений, показанные на втором рисунке.

Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.

Диагональ куба в квадратный корень из трёх раз больше его стороны:

Четыре сечения куба являются правильными шестиугольниками (одно из них показано на рисунке) – эти сечения проходят через центр куба перпендикулярно четырём его диагоналям.

У куба девять плоскостей симметрии:

Пирамида

Пирамидой (например, SABCDE ) называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE ) – основания пирамиды, точки ( S ), не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.

Поверхность пирамиды состоит из основания (пятиугольник ABCDE ) и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды:

Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.

Высотой пирамиды ( SО ) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания.

α – угол наклона бокового ребра SA пирамиды к плоскости её основания;

β – угол наклона боковой грани ( SED ) пирамиды к плоскости её основания.

Основание высоты пирамиды является центром окружности, описанной около основания пирамиды, тогда и только тогда, когда выполняется одно из условий:

Основание высоты пирамиды является центром окружности, вписанной в основание пирамиды, тогда и только тогда, когда выполняется одно из условий:

Объём пирамиды равен трети произведения площади основания на высоту пирамиды:

Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания:

Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды.

Плоскость, которая пересекает пирамиду и параллельна её основанию, делит её на две части:

многогранник, называемый усеченной пирамидой ( AВСA₁В₁С₁ ).

Основания усеченной пирамиды представляют собой подобные многоугольники, боковые грани – трапеции.

Высота усеченной пирамиды ( ОО₁ ) – это расстояние между плоскостями её оснований.

Если S₁ и S₂ – площади оснований усечённой пирамиды и h – её высота, то для объёма усеченной пирамиды верно:

Пирамида (например, SABCD ) называется правильной, если ее основанием является правильный многоугольник ( ABCD – квадрат ), а основание высоты совпадает с центром этого многоугольника ( О – центр описанной и вписанной окружностей основания).

Осью правильной пирамиды называется прямая, содержащая ее высоту.

Боковые ребра правильной пирамиды равны.

Боковые грани правильной пирамиды – равные равнобедренные треугольники.

Высота боковой грани правильной пирамиды ( SL ), проведенная из ее вершины к стороне основания, называется апофемой.

Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему:

Усеченная пирамида (например, АВСDA₁В₁С₁D₁ ), которая получается из правильной пирамиды, также называется правильной.

Правильные многогранники

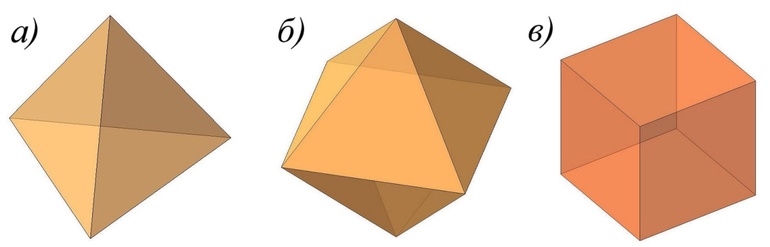
Тетраэдр Куб Октаэдр

Додекаэдр Икосаэдр

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.

Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.

У куба (правильный гексаэдр) все грани – квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами.

У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.

У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.

У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 13. Многогранники

Перечень вопросов, рассматриваемых в теме:

Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.

Грани многогранника – многоугольники, ограничивающие многогранники.

Ребра многогранника – стороны граней многогранника.

Вершины многогранника – концы ребер многогранника (вершины граней многогранника).

Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.

Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.

Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.

Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)

Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)

Открытые электронные ресурсы:

Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.

Теоретический материал для самостоятельного изучения

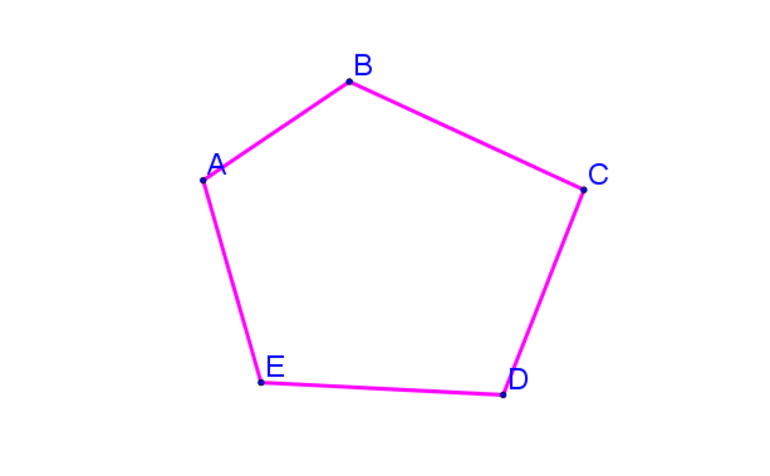
К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.

Б)

Рисунок 1 – разные подходы к определению многоугольника

Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.

В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.

Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)

Рисунок 2 – изображение октаэдра

Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».

Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).

Рисунок 3 – Виды многогранников

Сумма плоских углов при вершине выпуклого многогранника

Рисунок 4 – сумма плоских углов пи вершине многогранника

Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.

Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.

Примеры и разбор решения заданий тренировочного модуля

Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.

Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.

Задание 2. Сопоставьте геометрическим фигурам их вид

Б) пространственная фигура

Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.

Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б

Источник

Основные понятия

Определение многогранника включает в себя такое понятие, как геометрическое тело, созданное из плоских многоугольников. Их число конечное. От формы каждого из них напрямую зависят свойства итоговой фигуры. Их делят на 2 типа:

Поскольку многогранники рассматриваются в трехмерном евклидовом пространстве, они относятся к стереометрии. А их многоугольники лежат в двумерной плоскости, что относится к планиметрии. Поэтому основные свойства и понятия формируются, включая в себя обе эти науки.

Параметры фигуры

Правильные многогранники

Правильные многогранники — фигуры, грани которых представляют собой многоугольники с равными углами и сторонами. Также они называются Платоновыми телами. Всего существует 5 соответствующих тел, подробные характеристики которых представлены в таблице.

Правильные многогранники изучались древними греками. Однако первые модели в орнаменте и по отдельности появились намного раньше. Например, археологами были найдены вырезанные каменные шары в Шотландии, которые датируются поздним неолитом (соответственно, за 1000 лет до жизни и деятельности Платона).

Призма и ее особенности

Геометрическое тело называют прямым, если каждое ребро лежит перпендикулярно основанию. Также они становятся высотами. Когда грани идентичны, многоугольник считается правильным, и его диагональное сечение образует параллелограмм.

Характеристики параллелепипеда

Параллелепипед — многогранник, основанием и гранями которого является параллелограмм. Фигура характеризуется как неправильная. Основные характеристики:

Когда все грани параллелограмма являются прямоугольными, фигура характеризуется, как прямоугольная. Длина каждого ребра считается линейным размером. У такой фигуры есть три измерения. При этом справедлива формула d² = a² + b² + c². При расчетах руководствуются и другими. Для объема : V = abc, для площади многогранника: S=2·(ab+ bc +ac).

Пирамида и ее величины

Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:

Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.

Источник

Лекция по дисциплине » Математика» по теме «Многогранники»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

РАЗДЕЛ 10. МНОГОГРАННИКИ

1. Понятие многогранника

1. Понятие многогранника

2. Виды многогранников

3. Элементы многогранников

4. Площадь поверхности многогранников

5. Объем многогранника

P Многогранником называют геометрическое тело,

поверхность которого есть объединение

конечного числа многоугольников (рис.1).

Обозначение : ABCDEF – шестигранник (перечисление всех вершин)

Многоугольники, составляющие поверхность многогранника называют его гранями:

Стороны этих многоугольников называются ребрами:

Вершины многоугольников- называются вершинами многогранника:

Отрезок, соединяющий две вершины многогранника, не принадлежащие одной грани, называют диагональю многогранника.

Многогранник может быть выпуклым и невыпуклым.

Мы будем рассматривать преимущественно выпуклые многогранники, для краткости опуская слово «выпуклые».

Примеры правильных многогранников

1 Правильный тетраэдр

2) Правильный гексаэдр

3) Правильный октаэдр

5) Правильный икосаэдр

Площадью поверхности многогранника называют сумму площадей всех его граней.

Площадь каждой грани находится по формуле в зависимости от ее вида.

СМ. справочник стр 25

РАЗДЕЛ 10. ГЕОМЕТРИЯ НА ПЛОСКОСТИ.

, где

где — радиус вписанной окружности, — радиус описанной окружности

Определение :

Призмой называется многогранник, который

состоит из двух равных плоских многоугольников, лежащих

в разных параллельных плоскостях, и боковые грани

которого являются параллелограммами

А1А2…А _n B 1 B 2… B_n – призма

(сначала перечисляем вершины нижнего основания, затем – верхнего)

Еще об элементах призмы :

Диагональ призмы соединяет две вершины, не лежащие в одной плоскости.

Высота призмы –это перпендикуляр, опущенный из верхнего основания на нижнее основание.

Боковая поверхность – сумма площадей

Р_┴сеч— периметр перпендикулярного сечения

Полная поверхность – сумма двух

площадей оснований и площади боковой

S _полн – площадь полной поверхности

Перпендикулярное (ортогональное) сечение –

пересечение призмы и плоскости, перпендикулярной

боковому ребру призмы.

Объем призмы равен произведению площади

основания призмы, на высоту.

Основание – произвольный многоугольник

Боковые грани – прямоугольники

Основание – правильный многоугольник

Боковые грани – прямоугольники

НАКЛОННАЯ призма

Основание – произвольный многоугольник

Боковые грани – параллелограммы

П А Р А Л Л Е Л Е П И П Е Д

НАКЛОННЫЙ параллелепипед

основания–параллелограммы

Бок. грани–параллелограммы

Бок.ребро – не высота

S _полн = S бок+2 S осн

ПРЯМОЙ параллелепипед

Бок. грани – параллелограммы

S полн = = S бок+2 S осн

ПРЯМОУГОЛЬНЫЙ параллелепипед

В основании – прямоугольник

Боков.грани – прямоугольник

Все грани – квадраты

Определение :

Пирамида –это многогранник, одна из граней которого

(основание) – многоугольник, а остальные грани

(боковые) –треугольники, имеющие общую вершину

( вершина пирамиды)

В ее основании лежит

и высота НЕ всегда проходит

через центр основания

В ее основании лежит

и высота ВСЕГДА проходит

через центр основания

Свойства правильной пирамиды :

1. Все боковые грани – равные равнобедренные треугольники

2. Все боковые ребра равны между собой

3. Все апофемы равны

Формулы для вычисления площади поверхности и объема пирамиды

5. Усеченная пирамида

Усеченной пирамидой называется часть

пирамиды, заключенная между ее основанием

и сечением пирамиды, параллельным основанию

Элементы усеченной пирамиды :

Виды усеченной пирамиды :

Если в ее основаниях лежат произвольные подобные многоугольники

Если она является частью правильной пирамиды, в которой боковые грани – равные равнобедренные трапеции, а основания правильные подобные многоугольники.

Свойства правильной усеченной пирамиды :

1. Все боковые грани равные равнобокие трапеции

2. Все боковые ребра равны

3. Все апофемы равны

Формулы для вычисления площади поверхности и

объема усеченной пирамиды

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Проверочная работа для 6 класса по теме «Сравнение десятичных дробей»

Самостоятельная работа по теме «Сложение и вычитание десятичных дробей»

Проверочная работа для 6 класса по теме «Проценты»

Презентация интегрированного урока по математике и географии на тему «Температура воздуха»Температура воздуха

ОЛИМПИАДА ПО МАТЕАТИКЕ.ВО 2 КЛАССАХ

Карточки по математике «Числовые выражения». 2 класс

Методическая разработка учебного занятия «Определенный интеграл»

Памятка по математике (3 класс)

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5383232 материала.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Международный конгресс-выставка «Молодые профессионалы» пройдет с 12 по 14 декабря в Москве

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Госдума приняла закон об использовании онлайн-ресурсов в школах

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Минпросвещения намерено расширить программу ускоренного обучения рабочим профессиям

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник