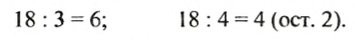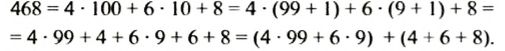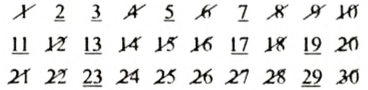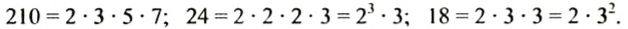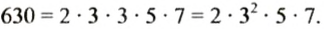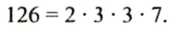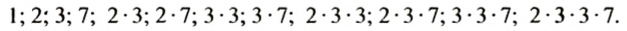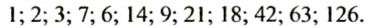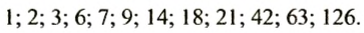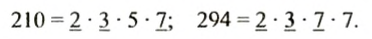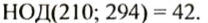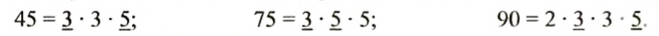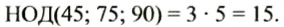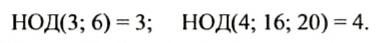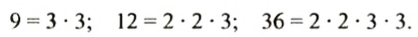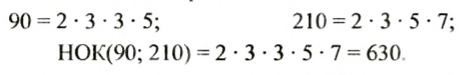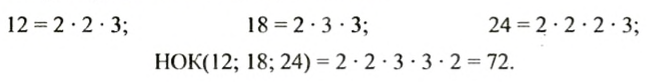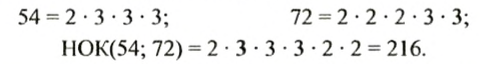Что называют делителем натурального числа простым делителем
Математика. 5 класс
Конспект урока
Делители натурального числа
Перечень рассматриваемых вопросов:
— разложение на простые множители.
Кратное число – это число, делящееся на данное целое число без остатка.
Простое число – это такое натуральное число, которое больше 1 и делится только на 1 и само на себя.
Составные числа – это непростые натуральные числа больше 1.
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 кл.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
«Все, что познаётся, имеет число, ибо невозможно ни понять ничего, ни познать без него», – сказал в своё время Пифагор. Эти слова очень кстати подходят к теме нашего урока «Делители натурального числа».
Выясним, что называют делителем.
Если натуральное число а можно разделить на натуральное число b, то это число b и будет делителем натурального числа а.
Мы уже знаем, что натуральные числа бывают простыми и составными.
Рассмотрим делители простых и составных чисел.
У простых чисел только два делителя –единица и само это число.
У составных чисел делителей больше.
Например, 3 – простое число, его делители 1 и 3.
14 – составное число, его делители 1, 2, 7 и 14.
Если делитель – простое число, то его называют простым делителем. Так, в наших примерах простыми делителями являются числа 2, 3, 7.
Можно ли представить любое составное число в виде произведения простых множителей? Ответ однозначный – да. Такое действие в математике называют разложение на простые множители.
Например, 36 – это произведение простых множителей:
36 = 2 · 2 · 3 · 3 = 2 2 · 3 2
Есть и другая форма записи разложения на простые множители любого числа.
Она представляет собой таблицу из двух колонок. В левую часть вначале записывается число, которое нужно разложить на простые множители, а в правую – простые делители этого числа. При этом следующим слева после исходного числа записывается число, которое является частным от деления на простое число справа. Так запись продолжается до тех пор, пока частное от деления не будет единицей.
Например, разложим число 100 на простые множители.
Разделим 100 на 2, частное равно 50;
50 разделим на 2, частное равно 25;
25 разделим на 5, частное равно 5;
5 разделим само на себя, получаем 1.
То есть простые множители числа 100:
100 = 2 · 2 · 5 · 5 = 2 2 · 5 2
Эти множители числа 100 и есть делители этого числа, только добавим ещё единицу и всевозможные произведения простых множителей.
Таким образом, делители числа 100 – это числа 1, 2, 4, 5, 10, 20, 25,100. Других делителей у числа 100 нет.
В дальнейшем нам понадобится ещё одно математическое понятие – кратное.
Кратное число – это число, делящееся на данное целое число без остатка. Иначе говоря, это исходное число, увеличенное в несколько раз.
Например, кратное числа 3 – это числа: 3, т. к. оно больше исходного числа 3 в один раз; 6, т. к. оно больше исходного числа 3 в 2 раза; 9, т. к. оно больше исходного числа 3 в 3 раза и т. д.
Если находить все делители натуральных чисел, то получится интересное свойство, о котором сейчас вы узнаете.
Например, найдём все делители числа 32.
Начиная с середины, все пары чисел при умножении будут давать 32.
Благодаря этому свойству, можно упростить поиск делителей числа. Для этого при поиске делителей достаточно найти «середину», а далее для нахождения остальных делителей числа остаётся найти частное от деления исходного числа на уже найденные делители.
У нас середина – это числа 4 и 8.
Найдём следующие делители:
№ 1. Какую из цифр 2, 3, 4 нужно подставить в число 5_ вместо пропуска, чтобы получить кратное числа 3?
Варианты ответа: 2, 3, 4.
Решение. Вспомним признак делимости на 3.Чтобы число делилось на 3, необходимо, чтобы сумма его цифр делилась на 3. Из представленных цифр подходит только 4, т.к. 5 + 2 = 7 – не делится на 3; 5 + 3 = 8 – не делится на 3; а 5 + 4 = 9 – делится на 3.
№ 2. Разложите произведение на простые множители 25 и 24.
Решение. Разложим отдельно числа 25 и 24 на простые множители, а затем найдём произведение всех полученных простых множителей от 24 и 25.
Волжский класс
Боковая колонка
Рубрики
Видео
Книжная полка
Малина для Админа
Боковая колонка
Опросы
Календарь
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
| « Ноя | ||||||
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | ||
7 класс. Алгебра. Никольский. Учебник. Ответы к стр. 13
Действительные числа
Натуральные числа
Разложение натуральных чисел на множители
Ответы к стр. 13
46. Что называют делителем натурального числа? Назовите делители числа 12.
Делителем натурального числа является такое число, на которое это натуральное число делится без остатка. Делители числа 12: 1, 2, 3, 4, 6, 12.
47. Что называют простым делителем натурального числа? Назовите простые делители числа 12.
Простым делителем натурального числа называют его делитель, который является простым числом. Простые делители числа 12: 2, 3.
48. Назовите все делители числа:
а) 17; б) 45; в) 113; г) 476; д) 32.
а) делители числа 17: 1, 17;
б) делители числа 45: 1, 3, 5, 9, 15, 45;
в) делители числа 113: 1, 113;
г) делители числа 476: 1, 2, 4, 7, 14, 17, 28, 34, 68, 119, 238, 476;
д) делители числа 32: 1, 2, 4, 8, 16, 32.
49. Найдите все простые делители числа:
а) 19; б) 54; в) 112; г) 232.
а) 19 | 19
1 |
19 = 1 • 19
Простые делители числа 19: 19.
б) 54 | 2
27 | 3
9 | 3
3 | 3
1 |
54 = 2 • 3 • 3 • 3 = 2 • 3 3
Простые делители числа 54: 2, 3.
в) 112 | 2
56 | 2
28 | 2
14 | 2
7 | 7
1 |
112 = 2 • 2 • 2 • 2 • 7 = 2 4 • 7
Простые делители числа 112: 2, 7.
г) 232 | 2
116 | 2
58 | 2
29 | 29
1 |
232 = 2 • 2 • 2 • 29 = 2 3 • 29
Простые делители числа 232: 2, 29.
50. Напишите пять натуральных чисел, не имеющих других простых делителей, кроме 2 и 5, и пять натуральных чисел, не обладающих этим свойством.
Пять натуральных чисел, не имеющих других простых делителей, кроме 2 и 5:
2 • 5 = 10;
2 2 • 5 = 4 • 5 = 20;
2 3 • 5 = 8 • 5 = 40;
2 5 • 5 = 32 • 5 = 160;
2 • 5 3 = 2 • 125 = 250.
Пять натуральных чисел, имеющие другие простые делители 3 и 7:
3 • 7 = 21;
3 2 • 7 = 9 • 7 = 63;
3 • 7 2 = 3 • 49 = 147;
3 3 • 7 = 27 • 7 = 189;
3 2 • 7 2 = 9 • 49 = 441.
51. Приведите примеры натуральных чисел, имеющих делители 3 и 4. Какие делители, кроме указанных, имеют выбранные натуральные числа?
Натуральные числа, имеющие делители 3 и 4: 12, 24, 36.
Число 12 имеет также делители: 1, 2, 6, 12.
Число 24 имеет также делители: 1, 2, 6, 8, 12, 24.
Число 36 имеет также делители: 1, 2, 6, 9, 12, 36.
52. Приведите примеры натуральных чисел, не имеющих других простых делителей, кроме 3 и 5.
3 • 5 = 15;
3 2 • 5 = 9 • 5 = 45;
3 • 5 2 = 3 • 25 = 75.
53. Найдите все делители чисел: 2, 6, 12, 28, 48, 100.
2 | 2
1 |
делители числа 2: 1, 2;
6 | 2
3 | 3
1 |
делители числа 6: 1, 2, 3, 6;
12 | 2
6 | 2
3 | 3
1 |
2 • 2 = 4,
2 • 3 = 6
делители числа 12: 1, 2, 3, 4, 6, 12;
28 | 2
14 | 2
7 | 7
1 |
2 • 2 = 4,
2 • 7 = 14
делители числа 28: 1, 2, 4, 7, 14, 28;
48 | 2
24 | 2
12 | 2
6 | 2
3 | 3
1 |
2 • 2 = 4,
2 • 3 = 6,
2 • 2 • 2 = 8,
2 • 2 • 3 = 12,
2 • 2 • 2 • 2 = 16,
2 • 2 • 2 • 3 = 24
делители числа 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48;
100 | 2
50 | 2
25 | 5
5 | 5
1 |
2 • 2 = 4,
2 • 5 = 10,
2 • 2 • 5 = 20,
5 • 5 = 25,
2 • 5 • 5 = 50
делители числа 48: 1, 2, 4, 5, 10, 20, 25, 50, 100.
54. Найдите все простые делители чисел:
а) 4, 9, 15, 10, 24; б) 46, 50, 58, 99, 128;
в) 196, 254, 400, 625, 10 000; г) 7, 77, 777, 7777, 77 777.
а) 4 | 2
2 | 2
1 |
простые делители числа 4: 2;
9 | 3
3 | 3
1 |
простые делители числа 9: 3;
15 | 3
5 | 5
1 |
простые делители числа 15: 3, 5;
10 | 2
5 | 5
1 |
простые делители числа 10: 2, 5;
24 | 2
12 | 2
6 | 2
3 | 3
1 |
простые делители числа 24: 2, 3;
б) 46 | 2
23 | 23
1 |
простые делители числа 46: 2, 23;
50 | 2
25 | 5
5 | 5
1 |
простые делители числа 50: 2, 5;
58 | 2
29 | 29
1 |
простые делители числа 58: 2, 29;
99 | 3
33 | 3
11 | 11
1 |
простые делители числа 99: 3, 11;
128 | 2
64 | 2
32 | 2
16 | 2
8 | 2
4 | 2
2 | 2
1 |
простые делители числа 128: 2;
в) 196 | 2
98 | 2
49 | 7
7 | 7
1 |
простые делители числа 196: 2, 7;
254 | 2
127 | 127
1 |
простые делители числа 254: 2, 127;
400 | 2
200 | 2
100 | 2
50 | 2
25 | 5
5 | 5
1 |
простые делители числа 400: 2, 5;
625 | 5
125 | 5
25 | 5
5 | 5
1 |
простые делители числа 625: 5;
10 000 | 2
5000 | 2
2500 | 2
1250 | 2
625 | 5
125 | 5
25 | 5
5 | 5
1 |
простые делители числа 10 000: 2, 5;
г) 7 | 7
1 |
простые делители числа 7: 7;
77 | 7
11 | 11
1 |
простые делители числа 77: 7, 11;
777 | 3
259 | 7
37 | 37
1 |
простые делители числа 777: 3, 7, 37;
7777 | 7
1111 | 11
101 | 101
1 |
простые делители числа 7777: 7, 11, 101;
77 777 | 7
11 111 | 41
271 | 271
1 |
простые делители числа 77 777: 7, 41, 271.
55. Разложите на простые множители числа, т.е. запишите число в виде произведения степеней простых чисел:
а) 16, 18, 26; б) 35, 48, 72;
в) 144, 210, 800; г) 216, 343, 384;
д) 1024, 1728, 1575; е) 9225, 1001, 1739.
а) 16 | 2
8 | 2
4 | 2
2 | 2
1 |
16 = 2 4
18 | 2
9 | 3
3 | 3
1 |
18 = 2 • 3 2
26 | 2
13 | 13
1|
26 = 2 • 13
б) 35 | 5
7 | 7
1 |
35 = 5 • 7
48 | 2
24 | 2
12 | 2
6 | 2
3 | 3
1 |
48 = 2 4 • 3
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 |
72 = 2 3 • 3 2
в) 144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 |
144 = 2 4 • 3 2
210 | 2
105 | 3
35 | 5
7 | 7
1 |
210 = 2 • 3 • 5 • 7
800 | 2
400 | 2
200 | 2
100 | 2
50 | 2
25 | 5
5 | 5
1 |
800 = 2 5 • 5 2
г) 216 | 2
108 | 2
54 | 2
27 | 3
9 | 3
3 | 3
1 |
216 = 2 3 • 3 3
343 | 7
49 | 7
7 | 7
1 |
343 = 7 3
384 | 2
192 | 2
96 | 2
48 | 2
24 | 2
12 | 2
6 | 2
3 | 3
1 |
384 = 2 7 • 3
д) 1024 | 2
512 | 2
256 | 2
128 | 2
64 | 2
32 | 2
16 | 2
8 | 2
4 | 2
2 | 2
1 |
1024 = 2 10
1728 | 2
864 | 2
432 | 2
216 | 2
108 | 2
54 | 2
27 | 3
9 | 3
3 | 3
1 |
1728 = 2 6 • 3 3
1575 | 3
525 | 3
175 | 5
35 | 5
7 | 7
1 |
1575 = 3 2 • 5 2 • 7
е) 9225 | 3
3075 | 3
1025 | 5
205 | 5
41 | 41
1 |
9225 = 3 2 • 5 2 • 41
1001 | 7
143 | 11
13 | 13
1 |
1001 = 7 • 11 • 13
1739 | 37
47 | 47
1 |
1739 = 37 • 47
56. Сколько чисел от 1 до 100:
а) делится на 2; б) делится на 5;
в) делится на 2 и на 5; г) не делится на 2 и на 5?
а) 100 : 2 = 50 — чисел, делящихся на 2;
б) 100 : 5 = 20 — чисел, делящихся на 5;
в) 100 : (2 • 5) = 100 : 10 = 10 – чисел, делящихся на 2 и на 5;
г) 100 − 100 : (2 • 5) = 100 − 100 : 10 = 100 − 10 = 90 — чисел, не делящихся на 2 и на 5.
57. Сколько чисел от 1 до 100 не делится ни на 2, ни на 3?
100 : 2 = 50 – чисел, делящихся на 2;
100 : 3 = 33 1 /3 ≈ 33 – чисел, делящихся на 3;
100 : (2 • 3) = 100 : 6 = 16 2 /3 ≈ 16 – чисел, делящихся и на 2 и на 3;
50 + 33 – 16 = 67 – всего чисел, делящихся на 2 и на 3
100 − 67 = 33 — числа от 1 до 100, не делящихся ни на 2, ни на 3.
Делимость чисел в математике с примерами решения
Содержание:
Делимость чисел
Делители натурального числа
18 конфет можно разделить поровну между 3 детьми, дав каждому ребенку по 6. Это же количество конфет, не разрезая их, нельзя разделить поровну между 4 детьми. Если каждому ребенку дать по 4 конфеты, то останется 2. Запишем:
Число 18 делится на число 3 без остатка (еще говорят: 18 делится на 3). Число 3 называют делителем числа 18. Число 18 не делится без остатка на 4 (еще говорят: 18 не делится на 4). Число 4 не является делителем числа 18.
Любое натуральное число, на которое делится данное натуральное число, называют делителем этого числа.
Запишем все натуральные числа, на которые делится число 18 Такими числами являются 1,2,3,6,9, 18. Итак, число 18 имеет 6 делителей: 1,2, 3,6,9 и 18.
Число 1 имеет только один делитель — 1. Любое другое число, например, 23, обязательно имеет по крайней мере два делителя — число 1 и само число (23), причем I — наименьший делитель, само число (23) — наибольший.
Пример:
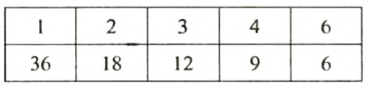
Найти все делители числа 36.
Решение:
Чтобы найти все делители числа 36, будем делить его на натуральные числа, начиная с 1: 36 : 1 = 36; 36 : 2 = 18; 36 : 3 = 12; 36 : 4 = 9; 36 : 5 = 7 (ост. 1); 36 : 6 = 6; 36 : 7 = 5 (ост. 1); 36 : 8 = 4 (ост. 4) и т. д.
Количество делений можно уменьшить. Найдя один делитель, сразу можем записать еще один, который является частным от деления числа 36 на этот делитель. Делители удобно записать так:
Итак, делителями числа 36 являются: 1, 2, 3,4, 6, 9, 12, 18, 36.
Признаки делимости на 2, 5 и 10
Как известно из изученного в пятом классе, чтобы умножить натуральное число на 10, нужно к записи этого числа дописать справа один нуль, например, 137 • 10 = 1370. Поскольку 10 является делителем числа 1370, то число 1370 делится на 10. В общем, на 10 делятся все числа, запись которых оканчивается цифрой 0.
Число, запись которого не оканчивается цифрой 0, например, 457, на 10 не делится.
Натуральное число, запись которого оканчивается цифрой 0, делится на 10.
Натуральное число, запись которого не оканчивается цифрой 0, не делится на 10.
Это правило называют признаком делимости на 10.
Найдем признак делимости на 5. Для этого разделим на 5 некоторые числа, например, 19, 82, 140, 245, 344, 515, 630, 1027.
Запишем в первый столбик те числа, которые делятся на 5, а во второй — те, которые не делятся на 5.
Какую вы заметили особенность чисел, которые делятся на 5; не делятся на 5?
Натуральное число, запись которого оканчивается цифрой 0 или 5, делится на 5.
Натуральное число, запись которого оканчивается цифрой, отличной от 0 или 5, не делится на 5.
Числа, которые делятся на 2, называют четными, а числа, которые на 2 не делятся, — нечетными. Например, 24 — число четное, поскольку оно делится на 2, а число 25 — нечетное, поскольку оно не делится на 2.
Однозначные числа 0, 2,4, 6, 8 являются четными, а числа 1, 3, 5, 7, 9 — нечетными.
Запись каждого числа, которое делится на 2, оканчивается однозначным четным числом. Если запись числа оканчивается однозначным нечетным числом, то оно не делится на 2.
Натуральное число, запись которого оканчивается однозначным четным числом, делится на 2.
Натуральное число, запись которого оканчивается однозначным нечетным числом, не делится на 2.
Для тех, кто хочет знать больше
Зная последнюю цифру в записи натурального числа, можно установить, делится ли оно на 2, 5 или 10.
Зная две последние цифры в записи натурального числа, можно ответить на вопрос, делится ли число на 4, на 25. А именно:
Натуральное число делится на 4, если число, образованное двумя его последними цифрами, делится на 4.
Натуральное число не делится на 4, если число, образованное двумя его последними цифрами, не делится на 4
Натуральное число делится на 25. если число, образованное двумя его последними цифрами, делится на 25.
Натуральное число не делится на 25, если число, образованное двумя его последними цифрами, не делится на 25.
Признаки делимости на 9 и на 3
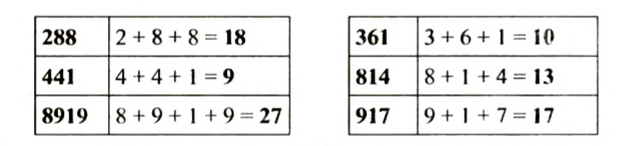
Найдем признак делимости на 9. Для этого разделим на 9 некоторые числа, например, 288, 361,441, 814. 917, 8919.
Запишем в первый столбик те числа, которые делятся на 9, а во второй — те, которые не делятся на 9.
Какую вы заметили особенность чисел которые делятся на 9; не делятся на 9?
Воспользуйтесь такой подсказкой: найдите сумму цифр каждого из этих чисел.
Какое свойство имеет сумма цифр тех чисел, которые делятся на 9?
Какое свойство имеет сумма цифр тех чисел, которые не делятся на 9?
Натуральное число делится на 9, если сумма его цифр делится на 9.
Натуральное число не делится на 9, если сумма его цифр не делится на 9.
Признак делимости на 3 аналогичен признаку делимости на 9.
Натуральное число делится на 3, если сумма его цифр делится на 3.
Натуральное число не делится на 3, если сумма его цифр не делится на 3.
Для тех. кто хочет знать больше
Признак делимости на 9, например, для числа 468, следует из таких преобразований:
Число 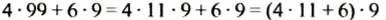
Простые и составные числа
Возьмем несколько натуральных чисел и найдем все их делители.
Мы видим, что числа имеют разное количество делителей. Число 1 имеет только один делитель — само это число. Числа 2, 3, 17 имеют по два делителя: 1 и само себя. Числа 4, 12,21 и 30 имеют больше, чем два делителя.
Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число. Число, имеющее более двух делителей, называют составным.
Итак, числа 2, 3, 17 — простые, а числа 4, 12, 21, 30 — составные. Число 1 не является ни простым, ни составным числом.
Если число имеет делитель, отличный от I и самого себя, то это число имеет более двух делителей и поэтому является составным. Число 12 475 — составное, так как имеет среди делителей, например, число 5.
Наименьшим простым числом является число 2. Наибольшего простого числа не существует. Все простые числа, кроме числа 2, являются нечетными.
Таблица простых чисел, которые не превышают 1000, находится на форзаце учебника.
Интересные рассказы
История математики знает имена ученых, которые приложили немало усилий для составления таблиц простых чисел. Первые такие попытки были сделаны еще в Древней Греции.
Если «высеять» все простые числа, не превышающие 30, то получим:
2, 3, 5, 7, II, 13, 17, 19, 23, 29 — первые 10 простых чисел.
Эратосфенов метод «высевания» простых чисел называют еще «решетом Эратосфена». Это связано с тем, что древние греки писали на папирусе или табличках, покрытых воском, и числа не вычеркивали, а выкалывали иголкой, после чего папирус или табличка напоминали решето.
В 1603 году итальянский математик Пьетро Катальди опубликовал в Болонье первую известную нам таблицу простых чисел меньше 750. Позже математики продвигались все дальше в глубь натурального ряда чисел, открывая все новые и новые простые числа.
Уже в 1770 голу немецкий математик Иоанн Генрих Ламберт (1728- 1777) опубликовал таблицу наименьших делителей всех чисел меньше 102 000, которые не делятся на 2, 3 и 5. Это была огромная работа. Не зря, призывая ученых продолжить составление таблицы, Ламберт гарантировал бессмертие тому, кто получит таблицу делителей до 1 000 000.
В середине XIX века в прессе появились сообщения, которые казались совершенно невероятными: Венская академия наук получила рукопись пражского математика Якуба Филиппа Кулика, содержащую таблицу деятелей чисел, не делящихся 2, 3 и 5, которую ученый расширил до 100 миллионов.
Редактор таблиц простых чисел Лемер посетил Вену и убедился, что в библиотеке академии хранится семь больших томов рукописных таблиц «Большой канон делителей всех чисел, которые не делятся на 2, 3 и 5, и простых чисел между ними до 100 330 201 Якуба Филиппа Кулика, публичного ординарного профессора высшей математики Пражского университета».
Якуб Филипп Кулик (1793 1863) родился во Львове. Окончив местную гимназию, он изучал философию, право и математику во Львовском университете, ас 1814 гола преподавал математику в лицее. С 1826 года Кулик стал профессором высшей математики Пражского университета. Много сил ученый отдал развитию культуры, науки и образования в родном крае. Он подарил много книг галицким гимназиям и Львовскому университету. Кулик является автором многих научных работ, но в историю математики он вошел как непревзойденный вычислитель и составитель математических таблиц.
Разложение натуральных чисел на простые множители
Составное число 24 можно записать как произведение двух множителей, например, 24 = 6•4. Говорят, что число 24 разложили на два множителя — 6 и 4. Числа 6 и 4 тоже можно разложить на множители: 6 = 3•2; 4 = 2•2. Теперь число 24 можно записать так: 24 = 3 • 2 • 2 • 2. В произведении 3 • 2 • 2 • 2 все множители являются простыми числами. Итак, число 24 разложили на простые множители.
Разложить число на простые множители означает записать его в виде произведения простых чисел. Любое составное число можно разложить на простые множители. Например:
Раскладывая числа на простые множители, надо найти простые делители этого числа. При этом можно использовать признаки делимости чисел. Чтобы разложить на множители большие числа, пользуются специальной схемой.
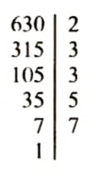
Пусть надо разложить на простые множители число 630.
Записываем это число и проводим справа вертикальную черту Наименьшим простым делителем этого числа является 2; записываем 2 справа or черты. Делим 630 на 2 и записываем частное 315 слева от черты под числом 630. Находим теперь наименьший простой делитель числа 315. Им является число 3, записываем его справа от черты. Делим 315 на 3, частное 105 записываем слева. Делим 105 на 3, получаем 35; 35 делим на 5, получаем 7. Число 7 простое, разделив его на 7, получим I. Разложение закончено.
Итак,
Пример:
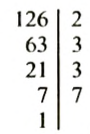
Найти все делители числа 126.
Решение:
Разложим число 126 на простые множители:
Делителями числа 126 являются: 1, простые числа 2, 3, 7 в полученном разложении и всевозможные произведения чисел 2, 3, 3, 7, то есть:
И так, делителями числа 126 являются:
Запишем все делители в порядке их возрастания:
Интересные рассказы
Расположение простых чисел
Утверждение о том, что каждое отличное от 1 натуральное число можно записать в виде произведения простых множителей и притом единственным способом, если не принимать во внимание порядок расположения сомножителей, является так называемой основной теоремой арифметики — одной из древнейших математических наук (в переводе с греческого «арифметика» — «искусство чисел»).
В соответствии с основной теоремой арифметики простые числа являются как бы кирпичами, из которых «строятся» натуральные числа. Этим и объясняется внимание к простым числам со стороны математиков всех времен. Еще древнегреческий математик Эвклид (ок. 365 ок. 300 г. до н. э.) доказал, что простых чисел есть бесконечно много, поэтому наибольшего простого числа не существует. Но еще до сих пор не изучены закономерности расположения простых чисел в натуральном ряду.
Талантливые математики многих стран стремились найти закон расположения простых чисел.
О свойствах простых чисел выдвинуто много интересных гипотез. Среди них самой интересной является гипотеза члена Петербургской академии наук Кристиана Гольдбаха (1690 1764), сформулированная так: любое натуральное число больше 5 является суммой трёх простых чисел
Свойства простых чисел можно наглядно представить так:
Перед нами откроется следующая картина.
Наибольший общий делитель
Выпишите все делители чисел 18 и 24 и подчеркните их общие делители
Общими делителями (они подчеркнуты) чисел 18 и 24 являются числа 1, 2, 3, 6, наибольшим из них является 6. Число 6 является наибольшим натуральным числом, на которое делятся и 18, и 24.
Наибольшее натуральное число, на которое делится каждое из данных чисел, называют наибольшим общим делителем этих чисел.
Итак, наибольшим общим делителем чисел 18 и 24 являегся число 6. Сокращенно это записывают так: НОД( 18; 24) 6.
В рассмотренном примере мы легко нашли наибольший общий делитель чисел, записав все делители каждого из них. Если числа большие и имеют много делителей, то нахождение наибольшего общего делителя этим способом является достаточно сложным.
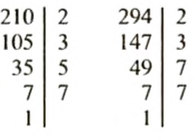
Рассмотрим еще один способ нахождения наибольшего общего делителя, взяв числа 210 и 294. Разложим каждое из этих чисел на простые множители:
Подчеркнем все общие простые множители в разложении данных чисел: 2, 3, 7. Числа 210 и 294 делятся на каждое из чисел 2, 3, 7 и на их произведение: 2•3•7 =42. Число 42 является наибольшим общим делителем чисел 210 и 294:
Назовите последовательность шагов при нахождении НОД двух чисел.
Для нахождения наибольшего общего делителя двух чисел можно разложить эти числа на простые множители и найти произведение их общих множителей.
По такому правилу можно находить наибольший общий делитель трёх и более чисел. Найдем, например, наибольший общий делитель чисел 45, 75 и 90. Разложим эти числа на простые множители и подчеркнем общие для всех чисел множители:
Итак,
Если среди данных чисел есть число, на которое делятся другие из данных чисел, то это число является наибольшим обидим делителем данных чисел. Например:
Два числа, наибольший общий делитель которых равен 1, называют взаимно простыми числами. Например, числа 16 и 27 являются взаимно простыми, так как их наибольшим общим делителем является 1.
Взаимно простые числа вообще имеют только один общий делитель — число 1. Поэтому, если два числа имеют общий делитель, отличный от 1, то они не взаимно простые. Например, числа 18 и 45 не являются взаимно простыми, так как имеют общий делитель 3.
Пример:
Какое наибольшее количество одинаковых букетов можно составить из 24 васильков и 32 ромашек, использовав все цветы?
Решение:
Из данных цветов можно, например, составить 2 букета. в каждом из которых будет 12 васильков и 16 ромашек. Нельзя составить три букета, так как 32 ромашки нельзя разделить на 3 одинаковые части. Можно составить четыре одинаковых букета, так как и 24 василька, и 32 ромашки можно разделить на 4 одинаковые части. Очевидно, что для решения задачи нужно найти наибольшее число, на которое можно разделить 24 василька и 32 ромашки, то есть найти наибольший общий делитель чисел 24 и 32. Поскольку НОД(24; 32) = 8, то можно составить самое большее 8 одинаковых букетов. Каждый такой букет будет состоять из 24 : 8 = 3 васильков и 32 : 8 = 4 ромашек.
Кратные натурального числа. Наименьшее общее кратное
Числа 36, 72, 180 делятся на 18. Говорят, что числа 36, 72, 180 кратны числу 18.
Любое натуральное число, которое делится на данное натуральное число, называют кратным данного числа.
Все числа, кратные числу 18, можно получить, умножая число 18 последовательно на числа 1,2, 3,4, 5.
18, 36, 54, 72, 90. — числа, кратные 18.
Каждое натуральное число имеет бесконечно много чисел, кратных ему, наименьшим из которых является само это число.
Запишите числа, кратные 9. и числа, кратные 12, и подчеркните их общие кратные.
Наименьшим общим кратным двух натуральных чисел называют наименьшее натуральное число, которое делится на каждое изданных чисел.
То, что наименьшим общим кратным чисел 9 и 12 является число 36, сокращенно записывают так: НОК(9; 12) = 36.
Разложим числа 9, 12 и их наименьшее общее кратное 36 на простые множители:
Мы видим, что разложение числа 36 можно получить, если разложение числа 9 умножить на 2 • 2. Числа 2 и 2 — это такие множители из разложения числа 12, которых нет в разложении числа 9
Назовите последовательность шагов при нахождении НОК двух чисел.
Чтобы найти наименьшее общее кратное двух чисел, можно каждое из них разложить на простые множители и разложение одного из чисел умножить на те множители другого числа, которых нет в разложении первого.
Найдем наименьшее общее кратное чисел 90 и 210.
Если одно из чисел делится на другое, то большее из них является наименьшим общим кратным этих чисел. Например, НОК(21; 63) = 63.
Наименьшим общим кратным двух взаимно простых чисел являегся произведение этих чисел. Например, НОК(8; 9) = 72.
Наименьшее общее кратное можно найти не только для двух, но и для трех и более чисел.
Например, для чисел 12, 18, 24 имеем:
Пример:
Найти наименьшее четырехзначное число, кратное 27.
Решение:
1000 — наименьшее четырехзначное число. Разделим его на 27: 1000: 27 = 37 (ост. 1).
27 • 38 = 1026 — наименьшее четырехзначное число, кратное 27.
Пример:
Шаг отца равен 72 см, а шаг сына — 54 см. Найти наименьшее расстояние, которое нужно пройти как отцу, так и сыну, чтобы каждый из них сделал при этом целое число шагов.
Решение:
Искомое расстояние в сантиметрах должно выражаться таким наименьшим числом, которое делится на 72 и на 54. Таким числом являемся наименьшее общее кратное этих чисел. Найдем НОК(54; 72):
Итак, искомое расстояние равно 216 см. На таком расстоянии отец сделает 216 : 72 = 3 шага, а сын — 216 : 54 = 4 шага.
Пример:
Найти наименьшее общее кратное чисел 15 и 12.
Решение:
Находим кратные большего из чисел и проверяем, делятся ли они на меньшее число: 15 не делится на 12; 15 • 2 = 30 — не делится на 12; 15 • 3 = 45 не делится на 12; 15 • 4 = 60 — делится на 12. Итак, НОК( 15; 12) = 60.
Памятка:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.