Что называют делителем числа кратным числа
Делитель и кратное в математике
Что такое делители и кратные числа
Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.
Выделяют следующие компоненты деления:
Делимое — число, которое делят на несколько частей.
Делитель — число, которое показывает, на сколько частей нужно разделить делимое.
Частное — число, которое является результатом деления.
Умножение частного на делитель дает делимое.
Чтобы получить делитель, нужно делимое разделить на частное.
Д е л и м о е = ч а с т н о е * д е л и т е л ь Д е л и т е л ь = д е л и м о е / ч а с т н о е
Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.
16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.
Делителем числа a называется такое число b, на которое a делится нацело.
Например, 9 : 4 = 2 (остаток 5 ).
В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.
Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9 : 4 = 2 (остаток 5 ) — число 4 не является делителем числа 9.
Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.
Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.
Тогда представим решение данной задачи в виде уравнения:
72 — целое число, без остатка.
Произведение делителей должно дать в результате 144:
72 * 2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.
Ответ: числа 2 и 72 — делители 144.
Число называют кратным, если оно делится на данное число нацело, без остатка.
Например, 15:3 нацело.
Тогда число 15 является кратным 3.
Слово «кратно» синонимично слову «делится».
Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».
Основные понятия и определения
Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.
Делится нацело = без остатка.
Наименьшим делителем любого числа является единица.
Наибольшим делителем числа является само число.
Делителем нуля будет любое число, но сам 0 делителем не будет.
При делении нуля на любое число получаем 0. А делить на ноль нельзя.
У единицы только один делитель — единица.
Другие числа, кроме 1, имеют не меньше двух делителей.
Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.
Наименьшее кратное числа является равным самому числу.
Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.
Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.
Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.
Чем отличаются друг от друга, как найти
Делитель отличается от кратного тем, что:
Чтобы найти делители числа, нужно данное число разложить на множители.
Разложить на множители — представить число в виде произведения целых чисел.
Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.
Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.
Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.
Примеры решения задач
Необходимо найти делители числа 14.
Решить задание можно двумя способами.
Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.
Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.
Ответ: делители числа 14: 1, 2, 7, 14.
Представим 14 в виде произведения чисел:
Делителями будут множители, так как можем разделить 14 нацело на каждый из них.
Ответ: делители 14: 1, 2, 7, 14.
Найдите три числа, кратных 7.
Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.
7 * 1 = 7 — семь кратно семи;
7 * 2 = 14 — 14 кратно 7;
7 * 3 = 21 — 21 кратно 7.
Ответ: числа, кратные 7: 7, 14, 21.
Самостоятельно проверьте, 225 кратно 3 или нет.
Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.
75 — целое число, при делении нет остатка. Тогда 225 кратно 3.
Найдите любое число, делителями которого являются числа 7 и 8.
Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:
Урок 1 Бесплатно Делители и кратные
Операция деления известна с давних времен.
Привычные нам сегодня обозначения операции деления появлялись постепенно, в более древние времена люди использовали другие знаки.
Первый из символов ( / ), в обиходе косая черта, впервые был применен в 1631 году в одной из работ англичанина Уильяма Отреда.
Со временем в математике стали использовать и знак ( : ). Его в своих работах использовал немецкий математик Готфрид Вильгельм Лейбниц (1646—1716)
При выполнении операции деления используют три математических составляющих:
Сегодня мы познакомимся с делителями и на связанном с ними понятии кратных.
Делители и кратные
Допустим, у вас есть 30 конфет и их надо разделить поровну шести друзьям.
В этом случае 6 друзей получат по 5 конфет, потому что 30 : 6 = 5
Если любое натуральное число делится без остатка на второе натуральное число, то первое называется кратным, а второе называют делителем.
Другими словами, 30 кратно 6, а 6 это делитель 30.
Могут быть и другие варианты решения задачи, которые зависят от данного нам условия.
Если друзей будет 7, тогда раздать всем равное количество конфет не получится, так как 30 без остатка на 7 не делится.
Значит, 30 не кратно 7, и 7 не является делителем 30
Натуральное число, на которое делится без остатка другое число, называется его делителем.
Само число 15 имеет четыре делителя: 1; 3; 5; 15, так как на каждое из этих чисел оно делится без остатка.
Натуральное число, которое делится на другое без остатка, называется его кратным.
Любое натуральное число имеет бесконечно много кратных.
Наименьшим из кратных натурального числа является само это число.
Например, кратными 4 будут числа: 4; 8; 12; 16; 20 и т.д.
У меня есть дополнительная информация к этой части урока!
Существуют числа, равные сумме всех их делителей, не считая самого числа.
Его делители 1, 2, 3.
Само число 6 не учитываем.
Сложив их, получим в сумме 6
К числам с таким свойством можно отнести еще 28 или 496
Пройти тест и получить оценку можно после входа или регистрации
Использование понятий делителя и кратного при решении примеров и задач
Любые математические понятия используются при решении примеров и задач, ответах на вопросы из жизни.
Разберем некоторые из них подробнее.
Пример 1
На сколько равных кучек можно разделить 24 ореха?
Решение:
Нужно выяснить все делители числа 24
Такими будут числа: 1; 2; 3; 4; 6; 8; 12; 24
Каждое из этих чисел будет являться ответом на поставленный вопрос, таким образом:
1 кучка из 24 орехов
2 кучки по 12 орехов
3 кучки по 8 орехов и т.д.
Пример 2
Напишите все двузначные числа, кратные 44
Решение:
Еще нам дано условие, что такие числа должны быть двузначными.
Значит, это два числа 44 и 88.
Оба они делятся на 44 без остатка, в чем можно легко убедиться: 44 : 44 = 1; 88 : 44 = 2
Пример 3
Какое число и кратно 15, и является делителем 15?
Решение:
Оно кратно самому себе и является для себя делителем.
Пример 4
В строю 300 солдат. Можно ли их разделить на 7 равных групп для проведения физической подготовки?
Решение:
Чтобы проверить, можно ли разделить 300 солдат на 7 равных групп, поделим число 300 на 7.
Имеем: 300 : 7 = 42 и в остатке 6. То есть 300 не делится нацело на 7.
Значит, разбить 300 солдат на 7 равных групп не получится.
Пример 5
Докажите, что число 70525 кратно числу 217.
Доказательство:
Выполним деление 70525 на 217 уголком.
Видим, что деление выполнено без остатка, значит, число 70525 кратно числу 217.
У меня есть дополнительная информация к этой части урока!
Делителем любого натурального числа является единица.
И правда, ведь на единицу делится любое натуральное число без остатка
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Раньше алгоритм деления в России выглядел совершенно иначе и не имел ничего общего с современным видом.
Например, деление могло получиться в виде полумесяца или по форме напоминать геометрическую фигуру- ромб.
Пусть требуется разделить 598432 на 678
Вот как выглядела запись деления:
1792
5603
5984/
5424
5424
1356
598432 верно разделено
Или разделить 9649378 на 5634:
59417
4015530
9649378
5634444
56333
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Делители и кратные
В этой статье будет рассмотрена тема: «Делители и кратные», привен конспект со всеми необходимыми определениями и правилами, а также разобраны примеры. Итак, поехали. С основными понятиям данной темы принято знакомится в курсе математики за 5 класс.
Если одно число делится на другое, то для описания их взаимосвязи используются слова «делитель» и «кратное».
Если одно натуральное число нацело делится на другое натуральное число, то первое число называют кратным второму числу, а второе число называют делителем первого числа.
Делитель числа
Если число a делится на число b, то число b называют делителем числа a.
Пример #1. Найдем все делители числа 24.
Два делителя числа 24 очевидны. Это 1 и 24. Далее будем проверять все числа подряд начиная с 2. Получим еще шесть делителей: 2, 3, 4, 6, 8, 12. Таким образом, число 24 имеет 8 делителей: 1, 2, 3, 4, 6, 8, 12, 24.
Этот перебор можно сократить, если отыскав один делитель, записать сразу же и другой, являющийся частным от деления числа 24 на найденный делитель. Такие пары делителей удобно записывать друг под другом
Часто при решении задач приходится находить общие делители двух и более чисел. Возьмем какие-нибудь два числа, например, 30 и 45. Найдем все делители каждого из них и подчеркнем их общие делители
Видим, что у чисел 30 и 45 есть общие делетели% 1, 3, 5, 15. Самый большой из них — чило 15. Его называют наибольшим общим делителем этих чисел.
С помощью перебора мы устновили, что НОД(30;45) = 15.
Наибольший общий делитель чисел a и b обозначают так: НОД(a;b).
Кратные числа
Когда одно число делится на другое, то для описания их взаимосвязи употребляют не только слово «делитель», но и еще слово «кратное».
Если число a делится на число b, то говорят, что число a — кратное числа b (или число a кратно числу b).
Например, число 45 делится на 9. Можно сказать, что число 9 является делителем 45 или что число 45 — кратное числа 9.
«Кратный» — слово русского происхождения. «Кратный» означает «известное число разов» — так говорится в толковом словаре стариных терминов. Но в современном языке мы используем слова с корнем «крат», например: одногратно, многократно.
С помощью перебора можно найти все делители числа. А как обстоит дело с кратным?
Эта последовательность, как и натуральный ряд, бесконечна, и все числа, кратные 10, выписать нельзя. Обратите внимание на то, как строится эта послдовательность: в ней первым идет число 10 и каждое следующее число на 10 больше предыдущего.
Примеры и задачи по теме: «Делители и кратные»
Пример #2. Найдем все делители и кратные числа 8.
Решение:
Два делителя числа 8 очевидны. Это 1 и 8. Далее будем проверять все числа подряд начиная с 2. Получим еще два делителя: 2, 4. Таким образом, число 8 имеет 4 делителя: 1, 2, 4, 8.
Далее найдем числа кратные 8. Для этого будем последовательно умножать 8 на 1, 2, 3, 4, 5 и т.д. Получим следующую последовательность: 8, 16, 24, 32, 40, … — все эти числа являются кратными 8.
Пример #3. Найдем все делители и кратные числа 36.
Решение:
Два делителя числа 36 очевидны. Это 1 и 36. Далее будем проверять все числа подряд начиная с 2. Получим следующие делителя: 2, 18, 3, 12, 4, 9, 6. Таким образом, число 36 имеет 9 делителей: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Далее найдем числа кратные 36. Для этого будем последовательно умножать 36 на 1, 2, 3, 4, 5 и т.д. Получим следующую последовательность: 36, 72, 108, 144, 180, … — все эти числа кратны 36.
Пример #4. Найдем все делители и кратные числа 9.
Решение:
Два делителя числа 9 очевидны. Это 1 и 9. Далее будем проверять все числа подряд начиная с 2. Получим следующие делителя: 3. Таким образом, число 9 имеет 3 делителя: 1, 3, 9.
Далее найдем числа кратные 9. Для этого будем последовательно умножать 9 на 1, 2, 3, 4, 5 и т.д. Получим следующую последовательность: 9, 18, 27, 36, 45, … — все эти числа кратны 9.
Пример #5. Найдем все делители и кратные числа 2.
Решение:
Два делителя числа 2 очевидны. Это 1 и 2. Больше делителей у числа 2 нет. Таким образом, число 2 имеет 2 делителя: 1, 2.
Далее найдем числа кратные 2. Для этого будем последовательно умножать 2 на 1, 2, 3, 4, 5 и т.д. Получим следующую последовательность: 2, 4, 6, 8, 10, … — все эти числа кратны 2.
Пример #6. Найдем число делителей и кратные числа 5.
Решение:
Два делителя числа 5 очевидны. Это 1 и 5. Больше делителей у числа 5 нет. Таким образом, число 5 имеет 2 делителя: 1, 5.
Далее найдем числа кратные 5. Для этого будем последовательно умножать 5 на 1, 2, 3, 4, 5 и т.д. Получим следующую последовательность: 5, 10, 15, 20, 25, … — все эти числа кратны 5.
Пример #7. Выбери все кратные числа 5: 1, 2, 5, 10, 15, 50, 51, 55.
Итак мы рассмотрели как находить делители и кратные для числа. Если у вас остались вопросы — задавайте их в комментария.
Пример #8. Выбери все кратные числа 10: 1, 2, 5, 10, 15, 50, 70, 85.
Решение:
Вспомним таблицу умножения на 10. Из представленных числу 10 кратны следующие: 10, 50, 70.
Итак мы рассмотрели как находить делители и кратные для числа. Если у вас остались вопросы — задавайте их в комментария.
Пример #9. Каждый шаг волшебных сапог-скороходов составляет 7 миль. Сколько миль в них можно пройти?
Варианты ответа: 4 мили, 14 миль, 17 миль, 23 мили, 28 миль, 56 миль.
Решение:
Для решения данной задачи следует найти все числа кратные 7. Это 14, 28 и 56.
Ответ: В волшебных сапогах-скороходах можно пройти 14, 28 или 56 миль.
Итак мы рассмотрели как находить делители и кратные для числа. Если у вас остались вопросы — задавайте их в комментария.
Делимость натуральных чисел.
Деление – это действие, обратное умножению. Рассмотрим более подробно деление натуральных чисел.
Натуральными числами называют числа, используемые для счета. Каждому количеству предметов счета соответствует некоторое натуральное число. Если предметов для счета нет, то используется число 0, но при счете предметов мы никогда не начинают с 0, и соответственно число 0 нельзя отнести к натуральным. Понятно, что наименьшим натуральное число является единица. Наибольшего натурального числа не существует, потому что каким бы большим не было число, всегда можно прибавить к нему 1 и записать следующее натуральное число.
Натуральное число k делится нацело на натуральное число n, если найдётся такое натуральное число m, для которого справедливо равенство k =n • m.
Или другими словами, чтобы разделить одно число на другое, надо найти такое трете число, которое при умножении на второе дает первое
число n — делителем числа k.
Числа 1, 2, 3, 6, 10, 15, 30 также являются делителями числа 30, а число 30 является кратным каждого из этих чисел. Заметим, что число 30 не делится нацело, например, на число 7. Поэтому число 7 не является делителем числа 30, а число 30 не кратно числу 7.
Выполнив действия по делению говорят: «Число k делится нацело на число n», «Число n является делителем числа k», «Число k кратно числу n», «Число k является кратным числа n».
Легко записать все делители числа 6. Это числа 1, 2, 3 и 6. А можно ли перечислить все числа, кратные числу 6? Числа 6• 1, 6• 2, 6• 3, 6• 4, 6• 5 и т. д. кратны числу 6. Получаем, что чисел, кратных числу 6, — бесконечно много. Поэтому перечислить их все невозможно.
Вообще, для любого натурального числа k каждое из чисел
является кратным числа k.
Наименьшим делителем любого натурального числа k является число 1, а наибольшим делителем — само число k.
Среди чисел, кратных числу k, наибольшего нет, а наименьшее есть — это само число k.
Каждое из чисел 21 и 36 делится нацело на число 3, и их сумма, число 57, также делится нацело на число 3. Вообще, если каждое из чисел k и n делится нацело на число m, то и сумма k + n также делится нацело на число m.
Каждое из чисел 4 и 8 не делится нацело на число 3, а их сумма, число 12, делится нацело на число 3. Каждое из чисел 9 и 7 не делится нацело на число 5, и их сумма, число 16, не делится нацело на число 5. Вообще, если ни число k, ни число n не делятся нацело на число m, то сумма k + n может делиться, а может и не делиться нацело на число m.
Число 35 делится без остатка на число 7, а число 17 на число 7 нацело не делится. Сумма 35 + 17 нацело на число 7 также не делится. Вообще, если число k делится нацело на число m и число n не делится нацело на число m, то сумма k + n не делится нацело на число m.
Делители и кратные
Попробуйте раздать поровну 15 тетрадей трем одноклассникам.
Это сделать легко, каждый получит по 5 тетрадей.

Но на шестерых одноклассников все 15 тетрадей разделить поровну нельзя.
Каждому достанется по две тетради и три тетради окажутся лишними.






Говорят, что число 15 кратно трем, а число 3 является делителем числа 15. Число 15 имеет четыре делителя: 1, 3, 5, 15.
Число 1 является делителем любого натурального числа.
Любое натуральное число имеет бесконечно много кратных.
(Здесь только первые 7 чисел натурального ряда, кратных трем (делятся на 3 без остатка). Продолжать можно до бесконечности.
число 15 кратно трем (делится без остатка на 3); число 15 кратное числа три; число три является делителем числа 15.
Делителем натурального числа n называют натуральное число, на которое n делится без остатка.
Например, число 3 называется делителем числа 18, так как число 18 делится на 3 без остатка.
Кратным натурального числа n называют натуральное число, которое делится на n без остатка.
Например, число 36 называется кратным числа 4 (36 кратно четырем), так как 36 делится на 4 без остатка.
Наименьшим из кратных натурального числа является само это число.
Свойства:
1) Если каждое из чисел 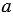 и и 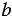 делится нацело на число делится нацело на число 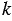 , то и сумма , то и сумма 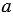 + + 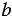 также делится нацело на число также делится нацело на число 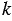 . . |
Пример: 15 : 5 = 3 и 35 : 5 = 7, а 15 + 35 = 50 и 50 : 5 = 10.
2) Если ни число 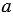 и ни число и ни число 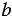 не делятся нацело на число не делятся нацело на число 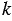 , то сумма , то сумма 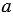 + + 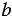 может делиться, а может и не делиться нацело на число может делиться, а может и не делиться нацело на число 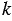 . . |
Примеры:
1) 13 и 7 не делятся на 5, а их сумма 13 + 7 = 20 делится на 5 (20 : 5 = 4).
2) 11 и 6 не делятся на 4 и их сумма 11 + 6 = 17 не делится на 4.
3) Если число 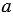 делится нацело на число делится нацело на число 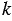 , а число , а число 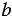 не делится нацело на число не делится нацело на число 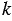 , то сумма , то сумма 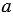 + + 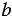 не делится нацело на число не делится нацело на число 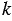 . . |
Пример: 15 + 25 = 40, слагаемое 15 и сумма 40 делятся нацело на 5 и также слагаемое 25 делится нацело на 5.
Поделись с друзьями в социальных сетях:




