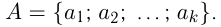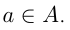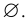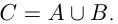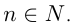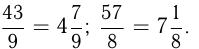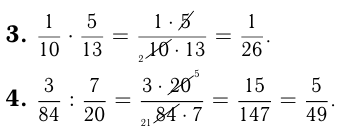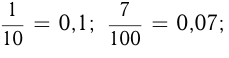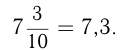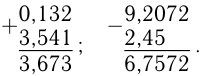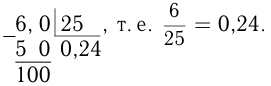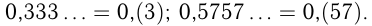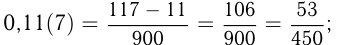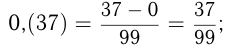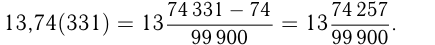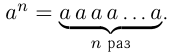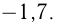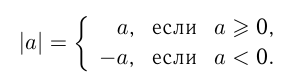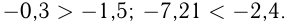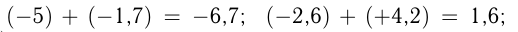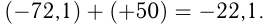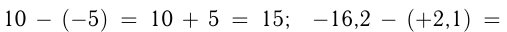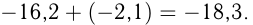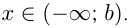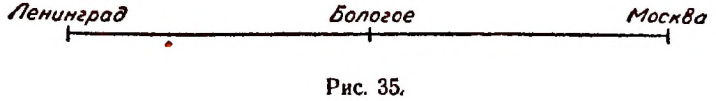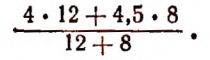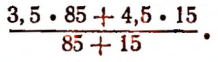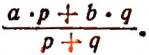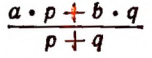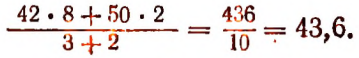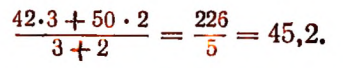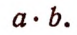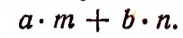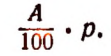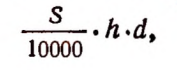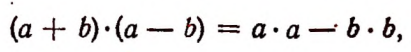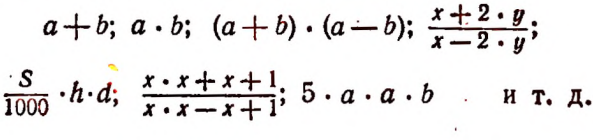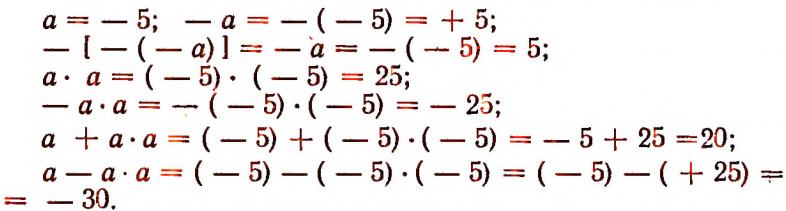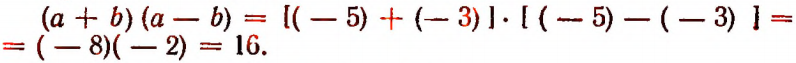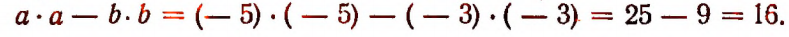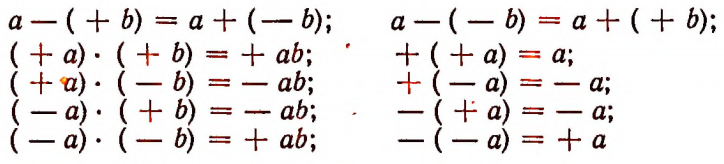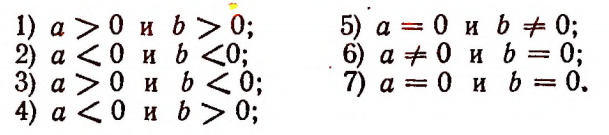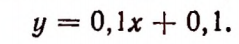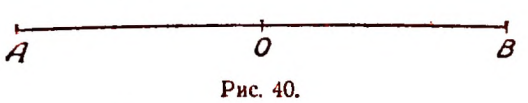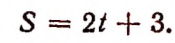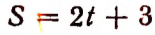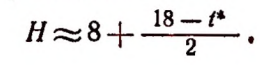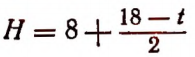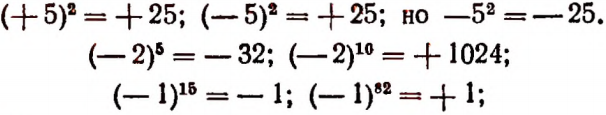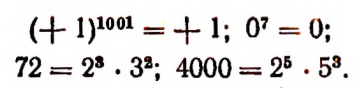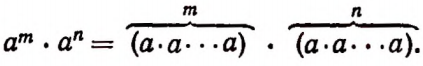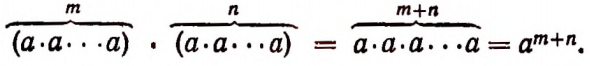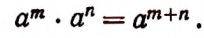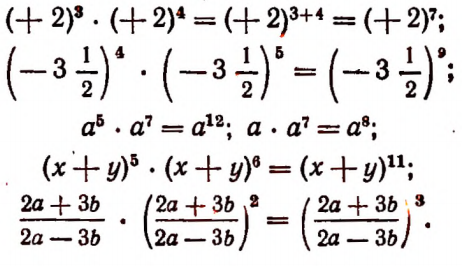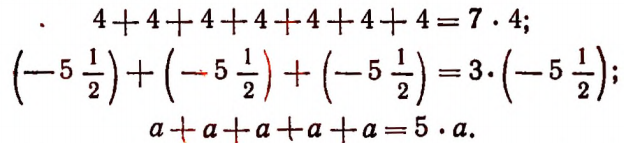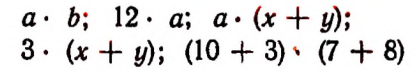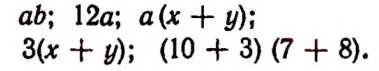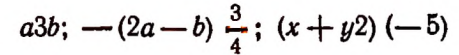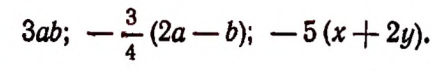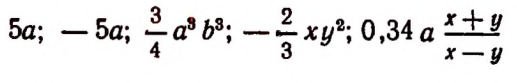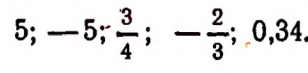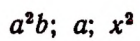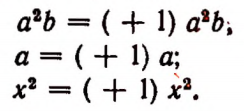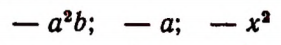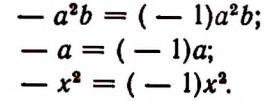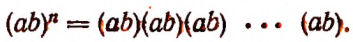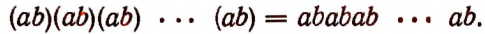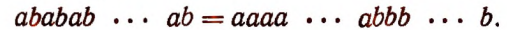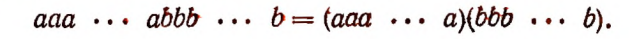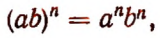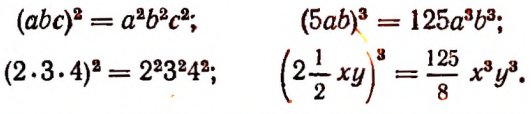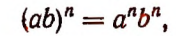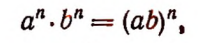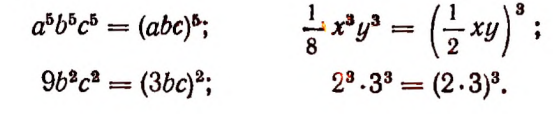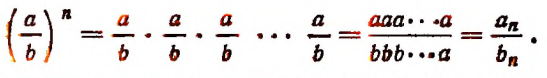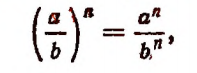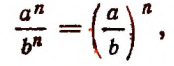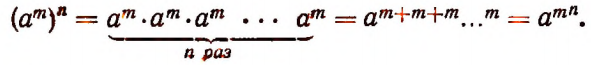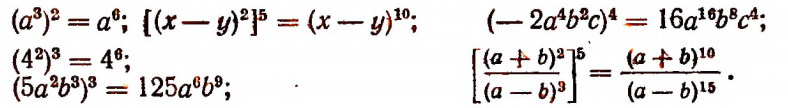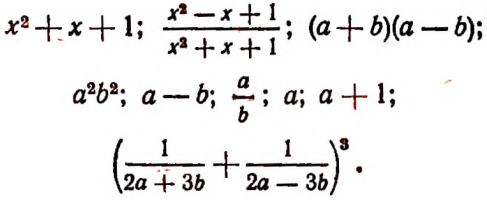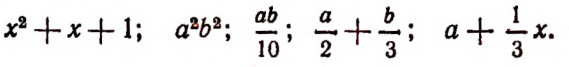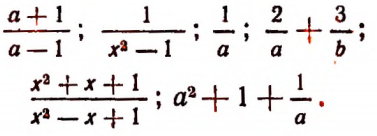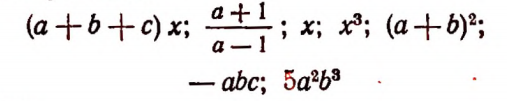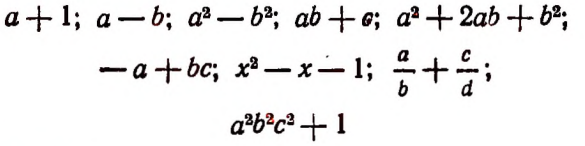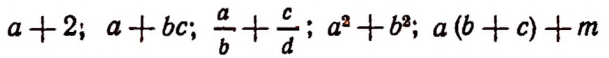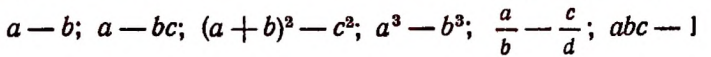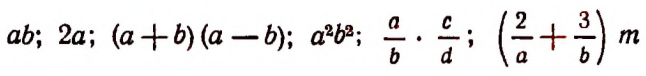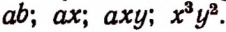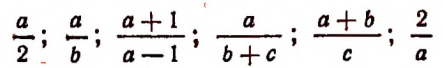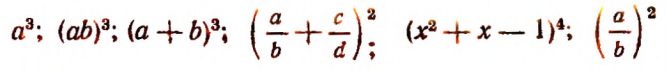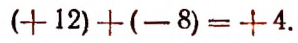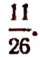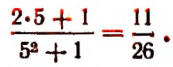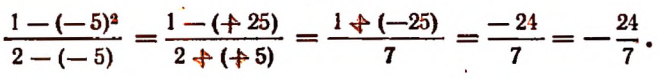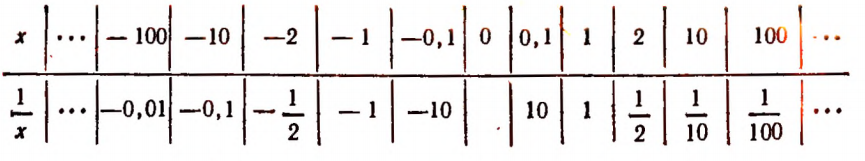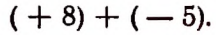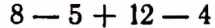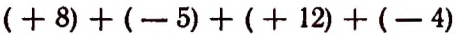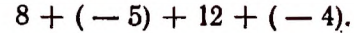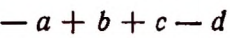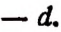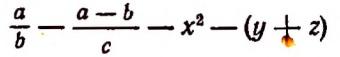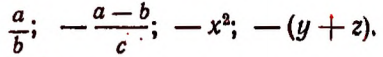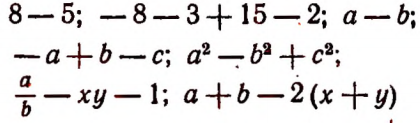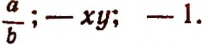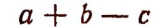Что называют числовым алгебраическим выражением
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
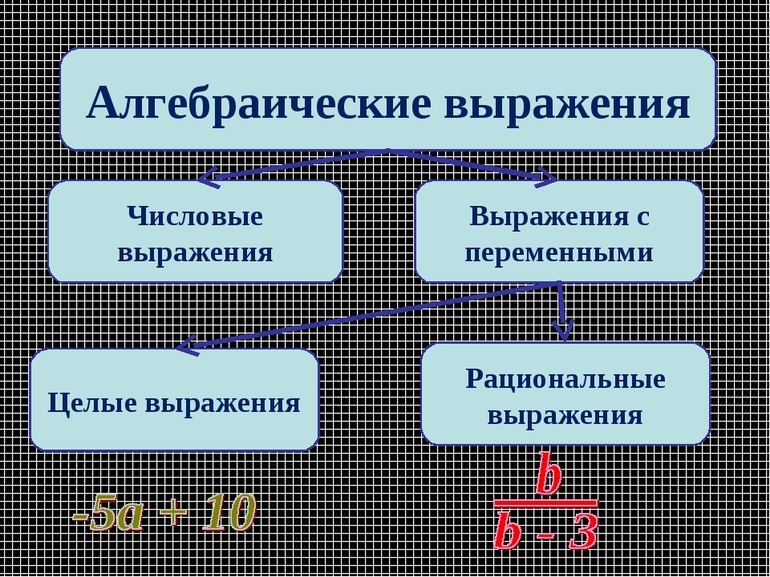
Алгебраические выражения

Всего получено оценок: 796.
Всего получено оценок: 796.
Алгебраические выражения начинают изучать в 7 классе. Они обладают рядом свойств и используются в решении задач. Изучим эту тему подробнее и рассмотрим примеры решения задачи.
Определение понятия
Какие выражения называют алгебраическими? Это математическая запись, составленная из чисел, букв и знаков арифметических действий. Наличие букв – это основное отличие числовых от алгебраических выражений. Примеры:
Буква в алгебраических выражений обозначает какое-либо число. Поэтому она называется переменной – в первом примере это буква а, во втором – b, а в третьем – с. Само алгебраическое выражение еще называют выражением с переменной.
Значение выражения
Значение алгебраического выражения – это число, получаемое в результате выполнения всех арифметических действий, которые указаны в этом выражении. Но, чтобы его получить, буквы необходимо заменить числами. Поэтому в примерах всегда указывают, какое число соответствует букве. Рассмотрим, как найти значение выражения 8а – 14 * (5 – а), если а = 3.
Подставим вместо буквы а число 3. Получаем следующую запись: 8 * 3 – 14 * (5 – 3).
Как и в числовых выражениях, решение алгебраического выражения проводится по правилам выполнения арифметических действий. Решим все по порядку.
Значение переменной называют допустимым, если при нем выражение имеет смысл, то есть возможно найти его решение.
Пример допустимой переменной для выражения 5 : (2а) – это число 1. Подставив его в выражение, получаем 5 : (2 * 1) = 2,5. Недопустимая переменная для данного выражения – это 0. Если подставить ноль в выражение, получаем 5 : (2 * 0), то есть 5 : 0. На ноль делить нельзя, значит, выражение не имеет смысла.
Тождественные выражения
Если два выражения при любых значениях, входящих в их состав переменных оказываются равны, их называют тождественными.
Пример тождественных выражений:
4 (а + с) и 4а + 4с.
Какие бы значения ни принимали буквы а и с, выражения всегда окажутся равны. Любое выражение можно заменить другим, тождественным ему. Этот процесс называют тождественным преобразованием.
Пример тождественного преобразования.
4 * (5а + 14с) – данное выражение можно заменить тождественным, применив математический закон умножения. Чтобы умножить число на сумму двух чисел, нужно это число умножить на каждое слагаемое и сложить полученные результаты.
Таким образом, выражению 4 * (5а + 14с) является тождественным 20а + 64с.
Число, стоящее в алгебраическом выражении перед буквенной переменной, называется коэффициентом. Коэффициент и переменная – это множители.
Решение задач
Алгебраические выражения используют для решения задач и уравнений.
Рассмотрим задачу. Петя придумал число. Для того, чтобы его отгадал одноклассник Саша, Петя сказал ему: сначала я прибавил к числу 7, затем вычел из него 5 и умножил на 2. В результате я получил число 28. Какое число я задумал?
Для решения задачи нужно загаданное число обозначить буквой а, а затем произвести все указанные действия с ним.
Теперь решим полученное уравнение.
Петя задумал число 12.
Что мы узнали?
Алгебраическое выражение – запись, составленная из букв, чисел и знаков арифметических действий. Каждое выражение имеет значение, которое находят путем выполнения всех арифметических действий в выражении. Буква в алгебраическом выражении называется переменной, а число перед ней – коэффициентом. Алгебраические выражения используют для решения задач.
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8
Математические термины
Алгебра — это наука, изучающая действия над числовыми и буквенными величинами. Кроме того, она занимается решениями уравнений и связанными с ними действиями. Под буквенными величинами обычно понимают конкретные или переменные числовые значения. Входящие в состав записи буквы могут иметь различные числовые величины. Например, в формуле S * 4 + 12 символом S может быть заменена известная или неизвестная величина или даже целое выражение.
Математики под алгебраическим выражением понимают запись, составленную со смыслом, состоящую из букв и цифр, обозначающих числа. При этом она может содержать скобки и знаки арифметических действий. Исходя из этого простейшего определения можно утверждать, что формулы 2 * k — s, 4 * (y — 3/2), 0,89 * a — g * (9a + 4b), a 2 и (29p — 56) / log (a + c) являются примерами алгебраических выражений. Так как буквы в записях обозначают различные числа, то их считают переменными, а само уравнение — выражением с переменной.
Если же значение переменной известно и его можно подставить на место буквенного обозначения, то результат, полученный после выполнения указанных в уравнении действий, называется ответом алгебраического выражения. Но если число, подставляемое вместо буквы, приводит к бессмысленности записи, то оно считается недопустимым. Из этого можно сделать вывод, что одна и та же алгебраическая запись при различных величинах букв может иметь отличные значения.
На практике приходится сталкиваться с довольно сложными и громоздкими алгебраическими выражениями, поэтому над ними приходится выполнять ряд действий, правил, законов или использовать свойства для упрощения записи.
Кроме определений здесь применяется понятие «тождественность». Под ним понимают два выражения, для которых при любых значениях переменных, входящих в их состав, будет справедливо их равенство, например, 56* (x+с) = 56 * x + 56 * с.
Эти два выражения можно заменить друг другом или, выражаясь математическим языком, — «выполнить тождественное преобразование».
Виды выражений
В школе на уроках алгебры приходится сталкиваться с различными видами выражений. Обычно они состоят из нескольких членов. В математике существует группирование, объединяющее сходные элементы. Обучение понятиям начинают в седьмом классе с того, что приводят следующие определения:
Многочлен всегда подразумевает выполнение действий. При описании понятия используют и такие термины, как коэффициент, член, степень. Во время работы с одночленами применяют тождественное их приведение к стандартному виду.
В нём выражение представляют как произведение числового множителя и натуральной степени разных переменных, например, 2 * a, −x * 3.
Выражения в алгебре могут быть следующих видов:
Все указанные виды относят к простым, но с 7 класса алгебраические выражения будут усложняться. Сложный вид записи обычно состоит из многочлена, включающего в себя извлечение корня, логарифмы и возведение в степень, например, ln (x 2 — 1) * tg ((x + p) / cos x). И хоть среди них попадаются перечисленные типы, их относят к общему виду.
Вычисление сложных выражений подразумевает выполнение преобразований, которые позволят проще решить задание и найти правильный ответ.
Алгебраические действия
Решая задачу, приходится выполнять те или иные преобразования. Чаще всего сложность задания определяется громоздкостью и объёмом соответствующих преобразований, поэтому в школе на уроках элементарной математики часто попадаются задачи на упрощения.
Основу всех алгебраических действий составляют три закона. Это правила, касающиеся сложения и умножения: переставное, соединительное и распределительное. Но наряду с ними применяют и формулы сокращённого умножения.
На начальном этапе обучения рекомендуется даже записать данные правила отдельно на листик и пользоваться им, пока применение законов не дойдёт до автоматизма. Вот некоторые практические рекомендации, решаться с которыми примеры будут намного легче:
Не стоит забывать и о такой операции, как деление многочлена. Для этого используют метод столбика. Заключается он в размещении слагаемых многочлена в порядке убывания степени переменной и разделения первого слагаемого числителя многочлена на первое слагаемое знаменателя.
Затем результат умножают на делитель и отнимают ответ от делимого.
Применение преобразований
Алгебраические выражения, показывающие, что одна величина больше другой или равна ей, называют уравнениями и равенствами. При этом их используют для составления формул, то есть для записи, выражающей зависимость между двумя или несколькими переменными. Это удобно, так как преобразования позволяют привести формулу к простому для запоминания виду.
При решении примеров важно знать все существующие методы. Какой из них применять, конкретно указать нельзя, всё зависит от личных предпочтений и опыта решения подобных заданий. Например, пусть нужно упростить сложное выражение (a 3 (b — c) + b 3 (c — a) + c 3 (a — b)) / (a 2 (b — c) + b 2 (c — a) + c 2 (a — b)).
Сначала можно попробовать разложить на множители делитель и делимое. Один из вариантов преобразования числителя следующий:
a 3 (b — c) + b 3 (c — a) + c 3 (a — b) = a 3 b — b 3 c — a 3 c + b 3 c + c 3 (a — b) = ab (a 2 — b 2 ) = ab (a 2 — b 2 ) — c (a 3 — b 3 ) + c 3 (a — b) = (a — b) (ab (a + b) — c (a 2 + ab + b 2 ) + c 3 = (a — b) (a 2 b — a 2 c + ab 2 — abc + c 3 — cb 2 ) = (a — b) (a 2 (b — c) + ab (b — c) — c (b 2 — c 2 ) = (a — b) (b — c) (a 2 — c 2 + ab — cb) = (a — b) (b — c) (a — c) (a + b + c).
По аналогии раскладывая знаменатель, можно прийти к результату: (a — b) (b — c) (a — c). В итоге получится равенство (a 3 (b — c) + b 3 (c — a) + c 3 (a — b)) / (a 2 (b — c) + b 2 (c — a) + c 2 (a — b)) = ((a — b) (b — c) (a — c) (a + b + c)) / ((a — b)(b — c)(a — c)) = a + b + c.
В числителе возможно выделить множитель (a — b) на том основании, что делимое равно нулю, когда a совпадает с b. Обычно в двух взаимно обратных операциях выполнение одной сложнее, чем другой. Это касается, в частности, выполнения умножения алгебраических выражений и разложения на множители или возведения в степень с извлечением корня. Например, легко увидеть, что (5 + 3 √2) 2 = 43 + 30 √2, но значительно труднее прочитать это равенство справа налево.
Следует помнить, что когда при решении задачи встречается выражение подкоренного вида √с + n * √k или √a + b√k, то необходимо попытаться добыть соответствующий корень. Если же это невозможно, то нужно воспользоваться подбором.
Если нужно упростить выражение √11 + 6 √ 2, то его можно представить как c + b √2. Следовательно, справедливо будет следующее равенство: 11 + 6 √2 = с 2 + 2b 2 + 2 cb √2. Поиск целых (рациональных) c и b приведёт к решению системы: a 2 + 2b 2 = 11, ab = 3.
При этом подобрать нужную пару целых легко: a = 3, b = 1, то есть можно записать равенство как √11 + 6√ 2 = 3 + √2.
Алгебраические выражения в математике с примерами решения и образцами выполнения
Число — это важнейшее математическое понятие. В математике некоторые понятия являются первичными, неопределяемыми. К ним относятся понятия натурального числа, точки, прямой и т.д. Натуральные числа — это числа, используемые для счета предметов: 1, 2, 3, …, п, …
Другим фундаментальным понятием математики является понятие множества. Принято говорить, что множество объединяет элементы по какому-либо признаку. Множества можно составлять из самых разнообразных объектов на основе различных признаков. Элементами множества могут быть как материальные объекты, так и абстрактные понятия, такие как числа, геометрические фигуры, символы и т. п. Если в роли элементов множества выступают числа, то оно называется числовым множеством. Множества чаще всего обозначаются большими латинскими буквами А, В, С, …, а их элементы — малыми латинскими буквами а, Ь, с, … Если множество А состоит из k элементов 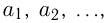
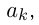
Если элемент а принадлежит множеству А, то пишут
Множество, которое не содержит элементов, называется пустым и обозначается
Пересечением множеств А и В называется множество С, которое состоит из элементов, входящих и в множество А, и в множество В, обозначается 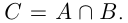
Множество натуральных чисел обозначают буквой N. Если какое-либо число n принадлежит множеству натуральных чисел, пишут
На множестве натуральных чисел определены операции сложения и умножения. Сумма и произведение натуральных чисел — также натуральные числа.
Вычитание натуральных чисел приводит не только к натуральным числам, но и к числам вида 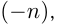
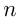
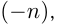
Обыкновенная дробь состоит из числителя и знаменателя, разделенных чертой, например 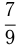
Важнейшим свойством дроби является то, что числитель и знаменатель дроби можно разделить на одно и то же число,т.е. дрооь можно сократить. Например, 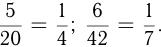
Если числитель дроби больше знаменателя, дробь — неправильная. 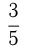
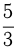
Число, состоящее из целой и дробной частей, — дробное число. Такое число можно превратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель дроби и добавить это произведение к числителю, а знаменатель оставить прежним. Например, 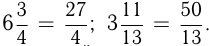
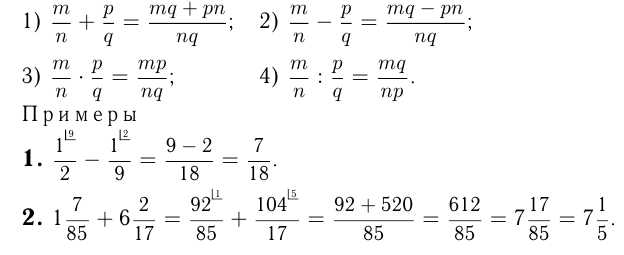
Дроби со знаменателями 10, 100, 1000 и т.д. называются десятичными дробями и записываются
При сложении и вычитании десятичных дробей числа записывают так, чтобы одинаковые разряды были записаны один под другим, а запятая — под запятой. Например,
При умножении десятичных дробей надо выполнить это действие, не обращая внимания на запятые, а затем в полученном произведении отделить справа запятой столько цифр, сколько их стоит после запятой в обоих множителях вместе.
При делении десятичных дробей на натуральное число делим сначала целую часть числа на это натуральное число, затем десятые, сотые и т.д. доли. Если целая часть меньше делителя, то в целой части частного получим 0. Например, 4,52 : 2 = 2,26; 1,28 : 4 = 0,32.
При делении на десятичную дробь надо в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, и затем делить на натуральное число.
Можно преобразовать десятичную дробь в обыкновенную и, обратно, обыкновенную дробь в десятичную. Для первого преобразования достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе — единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой. Например,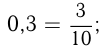
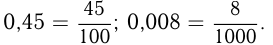
Отметим, что при этом может получиться бесконечная десятичная дробь. Например,
Бесконечная десятичная дробь, в которой, начиная с некоторого разряда, цифры повторяются, называется периодической. Записываются периодические дроби следующим образом:
Важно уметь переводить периодические дроби в обыкновенные. Для того чтобы обратить бесконечную периодическую десятичную дробь в обыкновенную, надо из числа, стоящего до 2-го периода, вычесть число, стоящее до 1-го периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после девяток дописать столько нулей, сколько цифр между запятой и 1-м периодом.
Например,
Рациональными называются числа, которые могут быть представлены в виде 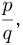
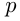
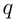
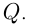
На множестве рациональных чисел определены операции сложения, вычитания, умножения, деления, возведения в натуральную степень, т. к. последняя операция сводится к умножению:
Возведение в отрицательную целую степень возможно для любого рационального числа, кроме 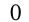
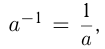
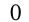
Прямую линию с выбранными на ней началом отсчета, еиничным отрезком и направлением называют числовой прямой, или числовой осью.
Два числа, отличающиеся друг от друга только знаком, называются противоположными. Например, 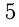
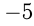
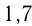
Каждому рациональному числу соответствует единственная точка на числовой прямой. Противоположные числа на числовой прямой расположены симметрично относительно нуля.
Модулем (абсолютной величиной) числа 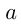
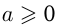
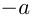
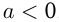
На числовой прямой 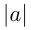
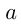
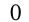
|0|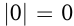
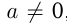
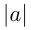
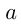
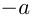
На числовой прямой правее расположено то из двух чисел, которое больше. Поэтому любое положительное число больше нуля и больше отрицательного числа; любое отрицательное число меньше нуля; из двух отрицательных чисел больше то, модуль которого меньше. Например,
Сумма двух рациональных чисел с одинаковыми знаками равна числу того же знака, модуль которого равен сумме модулей слагаемых. Сумма двух чисел с разными знаками равна числу, модуль которого равен разности большего и меньшего модулей этих чисел, а знак суммы совпадает со знаком того слагаемого, модуль которого больше. Например,
Разности двух рациональных чисел соответствует сложение уменьшаемого с числом, противоположным вычитаемому.
Например,
Произведение и частное двух рациональных чисел одного знака является положительным числом, произведение и частное двух чисел с разными знаками — число отрицательное.
Итак, множество 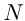
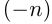
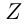
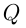
Числа, которые нельзя представить в виде 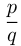
Рациональные и иррациональные числа вместе составляют множество действительных чисел, которое обозначается буквой 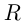
Итак, вся числовая прямая представляет собой множество действительных чисел, состоящее из рациональных и иррациональных чисел. Множество рациональных чисел включает в себя множество целых чисел и множество дробных чисел, множество целых чисел включает в себя множество натуральных чисел и множество противоположных им чисел.
На числовой прямой вводятся обозначения для числовых промежутков:
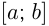
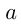
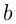
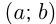
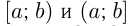
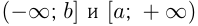
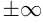
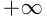
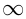
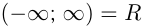
Если число 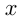
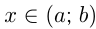
Эта теория с решениями взята со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
Употребление букв для обозначения чисел (буквенная символика)
Буквы употребляются и для обозначения чисел. Поясним на примерах, когда обозначать число буквой полезно и даже необходимо и когда это делать нет пользы.
Пример:
Когда дежурный по классу докладывает классному руководителю устно или письменно о числе учеников, не явившихся в этот день на занятия, то он произносит наименование этого числа или записывает его цифрами. Например, говорит «четыре» или записывает «4». В данном случае нет смысла число 4 обозначать буквой.
Пример:
Если же мы хотим сказать о числе учеников, которые в конце текущего учебного года окончат данную школу с золотой медалью, то мы можем это число обозначить какой-нибудь буквой, например буквой а, так как мы еще не знаем сколько таких учеников окажется. Если таких учеников окажется 3, то мы скажем, что а = 3, если их окажется 10, то а = 10, если же не окажется ни одного, то а = 0 и т. д.
Пример:
Пусть произведение двух чисел равно 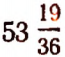
Пример:
Пусть паровоз движется без остановок со скоростью 80 км в час по Октябрьской железной дороге по направлению от Ленинграда к Москве и пусть в нуль часов (т. е. в полночь) проходит ст. Бологое. Расстояние от ст. Бологое в сторону Москвы будем считать положительным, а в сторону Ленинграда отрицательным (рис. 35)
При этих условиях расстояние от ст. Бологое до локомотива будет все время изменяться, а потому не может быть выражено каким-нибудь одним числом. Целесообразно величину этого расстояния обозначить какой-нибудь буквой, например буквой S. Тогда через час после полуночи S = 80; через 1 час 30 мин. S = 120 и т. д. За один час до полуночи S = — 80, за 1 час 30 мин. до полуночи S = —120 и т. д.
В алгебре любая буква, например а, может в одном случае обозначать собой число — 5, в другом, скажем, 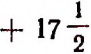
Если буквой а обозначено, скажем, число жильцов в доме, то в этом случае под буквой а нельзя подразумевать ни дробного, ни отрицательного числа.
Если буквой а обозначена длина веревки, то под буквой а нельзя подразумевать отрицательного числа.
Если число учеников, получивших золотую медаль, мы обозначили буквой а, то число учеников, получивших серебряную медаль, следует обозначить какой-либо другой буквой, например буквой b. Если мы захотим выразить число всех медалистов (и тех, и других), то напишем а + b.
Если при рассмотрении какого-либо вопроса одна и «га же буква, например буква x, употребляется несколько раз, то под значением этой буквы во всех случаях мы должны мыслить одно и то же. Например, если имеется частное (х + 2) : (х + 1). и если букве х, стоящей в делимом, мы припишем значение + 7, то букве х, стоящей в делителе, мы обязаны будем приписать то же самое значение + 7. Для обозначения чисел общепринято употреблять буквы преимущественно латинского и греческого алфавита. (Эти алфавиты помещены в конце вступительной статьи «Учащимся о математике»),
2. Возникает естественный вопрос: какие же обстоятельства, кроме указанных выше, побуждают нас к тому, чтобы употребление букв для обозначения чисел сделать систематическим и какая от этого получается польза? На этот вопрос очень трудно дать ответ, который, с одной стороны, был бы полным и конкретным, а с другой — оказался бы доступным пониманию лица, только что приступившего к изучению элементарной алгебры. Однако некоторые пояснения все же уместно сейчас сделать.
Пусть требуется решить, например, такую задачу. Смешали кофе двух сортов: 12 кг ценой по 4 руб. за 1 кг с 8 кг ценой по 4,5 руб. за 1 кг. Определить цену 1 кг смеси.
Решение этой задачи можно получить с помощью следующей последовательности действий:
На этом примере дана иллюстрация того, что решение всякой более или менее сложной арифметической задачи сводится к выполнению некоторой определенной последовательности действий над числами, данными в условии задачи. В итоге всех этих действий получается числовой ответ задачи. Если же мы эти действия не станем выполнять, а будем их только указывать, то в итоге получим некоторое арифметическое выражение, значение которого и будет ответом задачи.
Для сформулированной выше задачи получится следующее арифметическое выражение:
Значение этого выражения равно 4,2. Следовательно, цена смеси 4,2 руб. за 1 кг.
Решение задачи, записанное в виде арифметического выражения, имеет то преимущество, что позволяет видеть в собранной форме ту последовательность действий, которая решает данную задачу.
Если мы изменим числа, данные в условии задачи, то полученная в написанном выше арифметическом выражении последовательность действий не изменится. Так, например, если смешать 85 кг кофе ценой по 3,5 руб. за 1 кг с 15 кг ценой по 4,5 руб. за 1 /кг, то цена 1 кг смеси в рублях за 1 кг изобразится выражением:
Решим эту же задачу в общем виде, т. е. в предположении, что количества и цены двух сортов кофе какие угодно.
Пусть смешали р кг кофе ценой в а руб. за 1 кг с q кг ценой в b руб. за 1 кг. Тогда цена смеси в рублях за 1 кг изобразится выражением:
Конечно, числовое значение последнего выражения не будет определенным; оно будет зависеть от того, какие отдельные числовые значения мы станем давать буквам a, b, р и q. Однако наряду с этим выражение
имеет то преимущество перед простым числовым ответом, что оно, во-первых, является общим решением задачи, т. е. решением при любых данных, и, во-вторых, позволяет видеть в собранной форме план или правило решения поставленной задачи.
При изменении значений букв a, b, р и q или даже при изменении значения одной из этих букв будет изменяться, вообще говоря, и значение выражения
При а = 42; b = 50; р = 8 и q = 2 получим
При а = 42; b = 50; р = 3 и q = 2 получим
3. Рассмотрим несколько других примеров.
1. Пусть длина комнаты равна а м, а ширина — b м; тогда площадь комнаты в кв. м выразится произведением
2. Пусть магазин принял со склада m м сукна ценой по а руб. за 1 м и n м драпа ценой по b руб за 1 м. Тогда стоимость принятого товара в рублях изобразится следующей суммой двух произведений:
3. Пусть требуется найти р% от числа А.
Один процент числа А будет 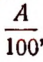
4. Площадь поперечного сечения цилиндрической колонны равна S кв. см, а высота — h м. Пусть 1 куб. см материала колонны весит d г. Тогда вес колонны в тоннах представится выражением
так как S кв. см составляют 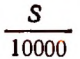
Таким образом, буквенное обозначение чисел позволяет получать решение задач в общем виде и тем самым выражать в краткой форме весь ход решения задачи.
4. Кроме того, буквенная символика позволяет кратко выражать законы, которым подчиняются числа. Например, вместо того, чтобы сказать, что сумма двух любых чисел не меняется от перемены мест слагаемых, достаточно написать:
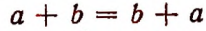
Рекомендуется сформулировать словами следующие законы:

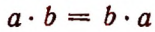

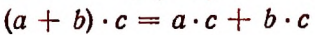
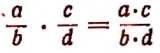
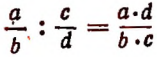
5. В дальнейшем мы увидим, что буквенная символика позволяет легко обнаруживать новые свойства чисел, имеющие общий характер. Например, в главе III будет показана справедливость равенства
в котором буквы а и b обозначают собой любые числа, а в главе VI мы встретимся уже и с применениями новых свойств чисел к решению практических задач.
Геометрия, физика, механика и другие науки выдвигают многочисленные задачи, решение которых нельзя осуществить без буквенной символики.
Алгебраическое выражение
1. В дальнейшем нам постоянно придется иметь дело с алгебраическими выражениями. Что же такое алгебраическое выражение?
Алгебраическим выражением называется совокупность чисел, соединенных между собой с помощью знаков действий. Эти числа могут быть изображенными с помощью цифр и с помощью букв.
Алгебраическое выражение может содержать и скобки, служащие для указания порядка действий.
Примеры алгебраических выражений:
Примечание:
Любое число или любую букву, обозначающую число, мы также будем считать алгебраическим выражением. Например:
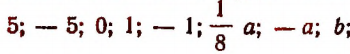
2. Приведем примеры нахождения числового значения алгебраического выражения.
Пусть под буквой а подразумевается число — 5, тогда
Пусть а = — 5 и b = — 3. Тогда
Пусть а= — 5 и b = — 3. Тогда
Замечание:
Выражение +а или просто а может иметь положительное, отрицательное и нулевое значения. Например, при
а = — 5 выражение +а имеет отрицательное значение — 5.
Выражение — а также может иметь положительное, отрицательное и нулевое значения. Например, при а = —5 выражение — а имеет положительное значение + 5.
3. Написанные ниже равенства
( _ а) • ( — Ь) = + аЬ\ — ( — с) = + а
Справедливость каждого из этих равенств легко доказать путем рассмотрения в отдельности каждого из следующих возможных случаев:
Равенство а = — а справедливо тогда и только тогда, когда а = 0. (Два противоположных числа равны друг другу лишь тогда, когда каждое из них равно нулю.)
Зависимости между величинами
1. При помощи алгебраических выражений можно представлять во многих случаях зависимости между величинами.
Примеры:
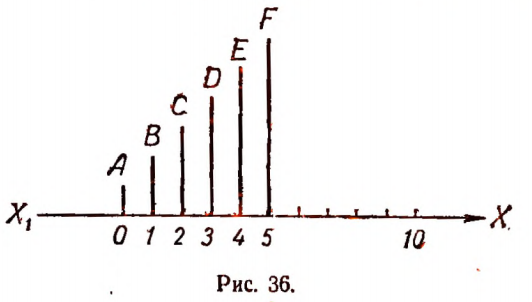
1. Проезд в такси стоит 0,1 руб. за включение счетчика и 0, 1 руб. за каждый километр пути. Если х есть число километров пути, а у стоимость проезда, выраженная в рублях, то зависимость величины у от величины х можно выразить равенством:
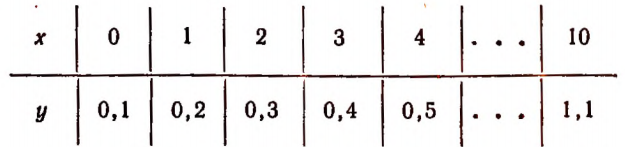
Составим таблицу значений у для нескольких отдельных значений х.
На рисунке 36 эта таблица изображена графически.
Вертикальными отрезками изображена стоимость в масштабе 5 мм 
По расположению точек А, B,C,D,E,F и т. д. являющихся концами вертикальных отрезков, можно составить наглядное представление о зависимости стоимости проезда от расстояния.
Эта зависимость (формула) точная; она известна из арифметики.
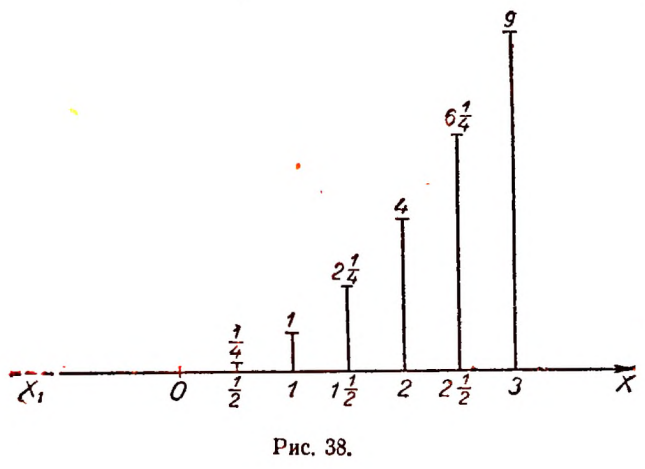
Графическое изображение этой таблицы дано на рисунке 38.
Масштаб по оси Х1Х: 1,5см 

Масштаб по оси Х1Х: 1,5см 

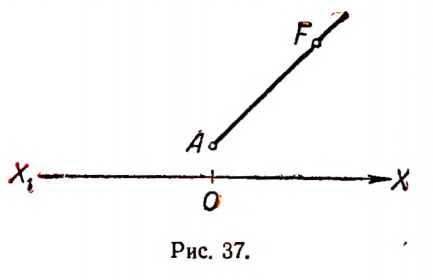
3. Условимся выражать расстояние от точки О по прямой А В (рис. 40) вправо- положительным числом, а влево отрицательным.
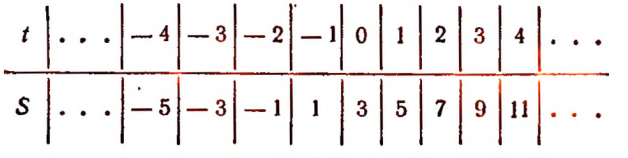
Условимся скорость точки, движущейся по прямой А В слева направо, выражать положительным числом, а при движении справа налево— отрицательным. Пусть точка движется по прямой А В равномерно со скоростью 2 м в сек. и в нуль часов находится от точки О на расстоянии 3 м. Расстояние от точки О до движущейся точки, выраженное в метрах, обозначим буквой S, а время в секундах — буквой t.
При этих условиях зависимость величины S от величины t выразится равенством
Составим таблицу значений величины S для нескольких отдельных значений величины t.
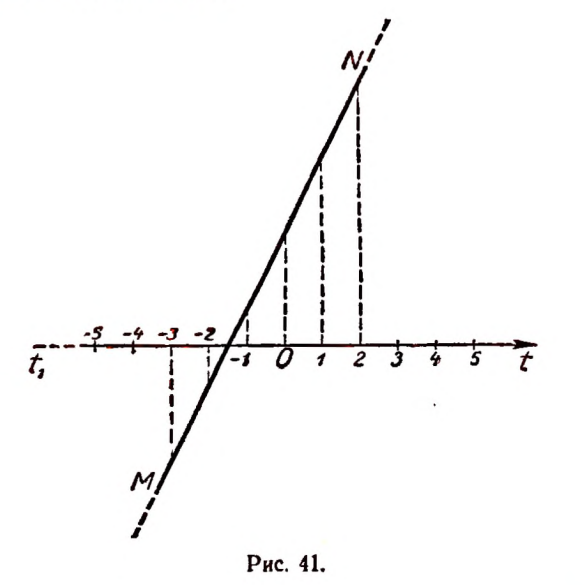
Графическим изображением зависимости
служит прямая MN на рисунке 41.
Масштаб по оси t1t : 0,5 см 

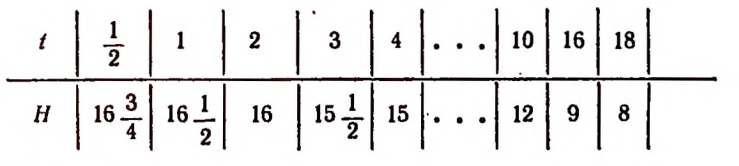
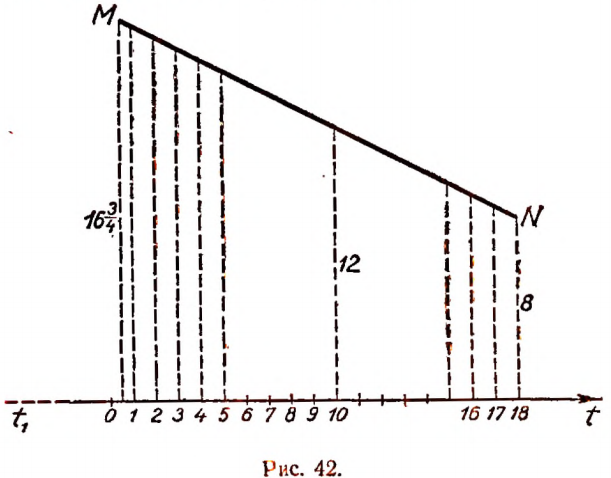
4. Если возраст человека в годах обозначить буквой t, а нормальное число часов ежедневного сна — буквой Н, то для возраста до 18 лет зависимость величины Н от величины t выразится приближенно следующим равенством:
Эта приближенная зависимость (формула) получена не теоретически, а на основе наблюдений и опытов врачей.
Составим таблицу значений величины Н для нескольких отдельных значений величины t.
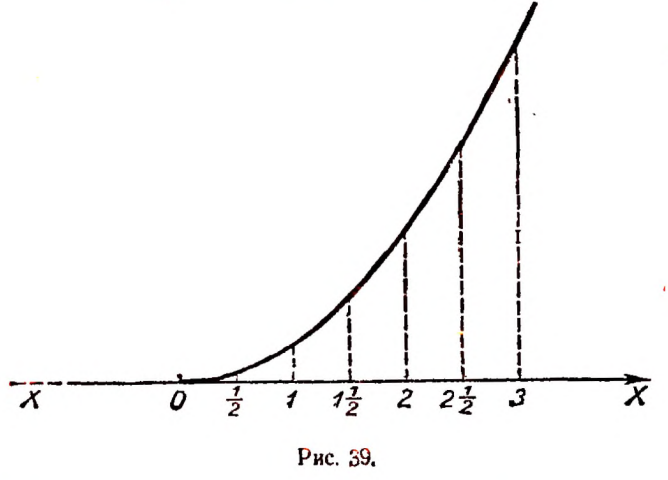
Графическим изображением зависимости
для значений t, больших или равных 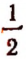
Масштаб по оси t1t : 2,5 мм 

5. Измеряя температуру воздуха в Москве через каждые два часа (с 11 час. 26 марта до 11 час. 27 марта 1957 года), получили следующую таблицу:
В первой строке указано время t в часах, а во второй — температура Т в градусах по Цельсию. За начало счета времени здесь принят момент нуль часов 27 марта. Время после этого момента выражено положительным числом, а до этого момента — отрицательным.
Например:
—13 обозначает момент времени 11 час. 26 марта;
—11 обозначает момент времени 13 час. 26 марта;
+ 11 обозначает момент времени 11 час. 27 марта.
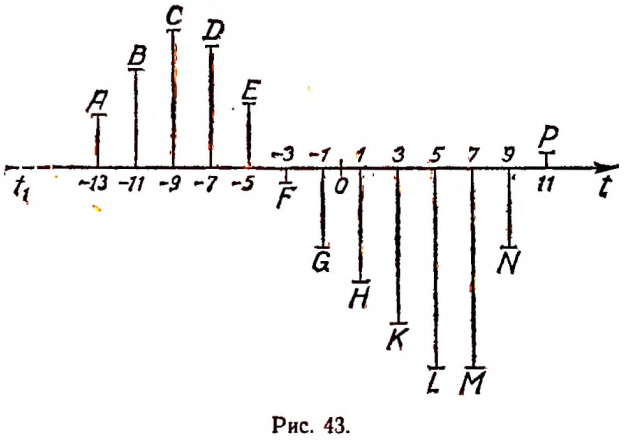
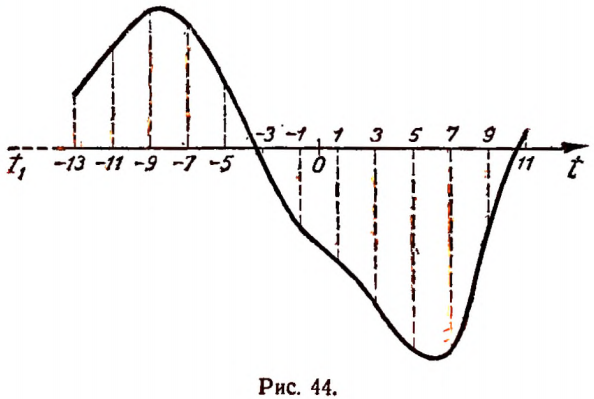
Числом 9 обозначаем момент времени 9 час. 27 марта и т. д. Графическое изображение этой таблицы дано на рисунке 43.
Масштаб по оси t1t: 0,5 см 

Соединяя на рисунке 43 точки А, В, С, D, Е, F, G, Н, К, L, М, N, Р плавной линией, получим график суточного изменения температуры (рис. 44).
В рассмотренном примере зависимость температуры Т от времени t получена путем непосредственного измерения температуры воздуха через равные промежутки времени.
Всякая зависимость, полученная путем наблюдений и опытов, называется эмпирической*.
* Прилагательное «эмпирический» происходит от греческого слова «ejmipiа», что означает «опыт»
Зависимости, приведенные в примерах 4 и 5, эмпирические.
Алгебраические выражения и действия над ними
Степень
1. Степенью называется произведение, составленное из одинаковых множителей.
Повторяющийся множитель называется основанием степени, а число всех одинаковых множителей называется показателем степени.
Например, произведение 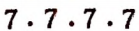
Произведение 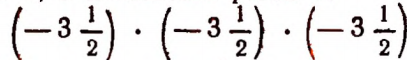
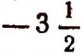
Эту степень принято обозначать символом 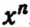
Степень 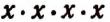
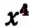
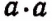
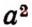
Выражение 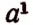
Действие, с помощью которого вычисляется значение степени, называется возведением в степень.
Замечание:
Обратим внимание на то, что символ 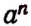
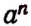
Умножение степеней с одинаковыми основаниями
По сочетательному закону умножения
Итак, при умножении степеней с одинаковыми основаниями их показатели складываются. Например:
Коэффициент
Сумму, составленную из одинаковых слагаемых, можно записать в виде произведения. Например:
Произведение 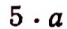
Например, вместо выражений
Определение:
Числовой множитель, выраженный цифрами, называется числовым коэффициентом.
Его принято ставить впереди буквенных множителей. Например, вместо выражений
числовыми коэффициентами будут соответственно
В каждом из выражений
числовой коэффициент равен 1, так как
В каждом из выражений
числовой коэффициент равен — 1, так как
Коэффициент, равный 1 и — 1, принято не писать. Вместо 1 • а пишут а. Вместо — 1 • а пишут — а.
Возведение в степень произведения частного и степени
Возведение произведения в степень
Чтобы возвысить произведение в степень, можно возвысить в эту степень каждый множитель в отдельности и полученные степени перемножить.
Иначе говоря, степень произведения равна произведению тех же степеней множителей. Действительно,
По сочетательному закону умножения
По переместительному закону
По сочетательному закону
что и требовалось доказать.
Примеры:
Поменяв местами левую и правую части равенства
т. е. произведение степеней с одинаковыми показателями равно степени, основанием которой служит произведение оснований данных степеней.
Примеры:
Возведение частного в степень
Чтобы возвысить частное в степень, достаточно возвысить в эту степень делимое и делитель и первый результат разделить на второй.
Короче говоря, степень частного равна частному степеней. Действительно,
Поменяв местами левую и правую части равенства
т. е. частное степеней с одинаковым показателем равно степени с тем же показателем и основанием, равным частному оснований данных степеней.
Возведение степени в степень
Чтобы возвести степень числа в новую степень, достаточно возвести это число в степень, показатель который равен произведению показателей степеней.
Примеры:
Классификация алгебраических выражений и порядок действий
Порядок действий в алгебраических выражениях сохраняется таким же, что и в арифметических выражениях.
Рациональное алгебраическое выражение
Определение:
Всякое алгебраическое выражение, в котором нет никаких других действий, кроме сложения, вычитания, умножения, деления и возведения в целую степень*, называется рациональным.
* Кроме этих пяти действий, в алгебре изучаются еще и другие математические действия.
Примеры рациональных выражений:
Целое выражение
Определение:
Если в рациональном выражении не содержится деление на буквенное выражение, то это рациональное выражение называется целым.
Примеры целых выражений:
Дробное выражение
Определение:
Выражение, содержащее деление на буквенное выражение, называется дробным.
Примеры дробных выражений
Одночлен
Определение:
Всякое выражение, в котором последнее действие не есть сложение или вычитание, называется одночленом.
Многочлен
Определение:
Выражение, в котором последнее действие есть сложение или вычитание, называется многочленом.
Определение типа любого выражения по последнему действию
1. Если в выражении последнее по порядку действие есть сложение, то это выражение называется суммой. Например, выражения
2. Если в выражении последнее действие есть вычитание, то это выражение называется разностью. Например, выражения
3. Если в выражении последнее действие есть умножение, то это выражение называется произведением. Например, выражения
Произведение, составленное из нескольких букв, принято записывать с соблюдением алфавитного порядка. Например, вместо 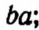
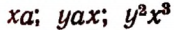
4. Если в выражении последнее действие есть деление, то это выражение называется частным. Например, выражения
5. Если в выражении последнее действие есть возведение в степень, то это выражение называется степенью.
Примечaние:
Если последнее действие есть возведение во вторую степень, то выражение называется квадратом, а если в третью, то кубом.
Например, выражение 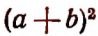

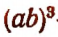
Полное название выражения
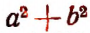

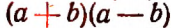


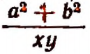
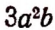
Обратим внимание на то, что полное название выражения 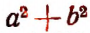


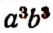
Если бы последнее действие было деление, то мы должны были бы начинать формулировку со слова «частное».
Числовое значение алгебраического выражения
Определение:
Числовым значением алгебраического выражения пои заданных значениях букв называется тот результат, который получится после замены букв их значениями и выполнения всех действий.
Примеры:
1. Числовым значением выражения а + b при а = + 12 и b = — 8 будет
2. Числовым значением 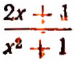
3. Числовое значение выражения 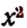
Очевидно, что значения выражения 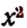
Очевидно, что значения выражения — 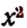
4. Значение выражения 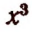
Значение выражения — 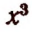
5. Значение выражения 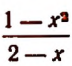
Таблица значений алгебраических выражений
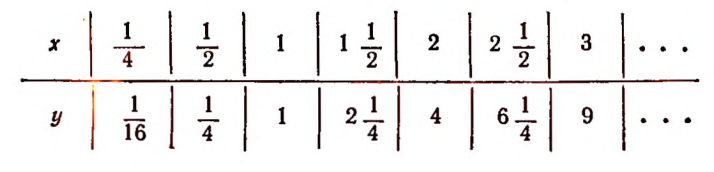
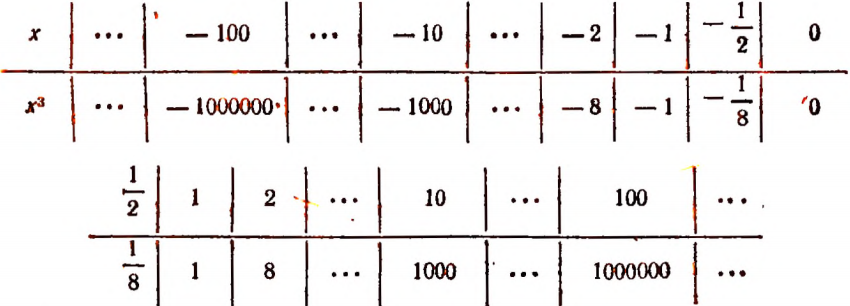
Составим следующую таблицу значений выражения 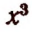
Очевидно, что при всех значениях буквы х, больших единицы, значения выражения 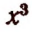
Если значение буквы х заключается между —1 и 0, то значение выражения 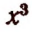
Если значение буквы х меньше — 1, то значение выражения 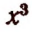
Составим таблицу значений выражения 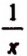
Выражение 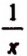
Составим таблицу значений выражения 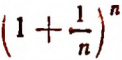
Примеры алгебраических выражений, теряющих смысл при некоторых значениях букв
Встречаются такие алгебраические выражения, которые теряют смысл при некоторых значениях входящих в них букв. Например, выражение 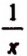
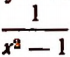
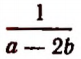
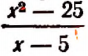
Все такие значения букв, при которых данное выражение не теряет смысла, называются допустимыми для данного выражения.
Для выражений 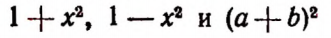
а) для 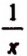
б) для 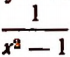
Примечание:
Значения буквы илb букв, обращающие знаменатель дроби в нуль, заслуживают особого внимания. В этих случаях дробь теряет смысл.
Алгебраическая сумма
Выражение 8—5 понимается в арифметике в единственном смысле, а именно кдк разность между числами 8 и 5.
В алгебре же это выражение можно понимать двояко:
либо как разность
Поэтому выражение 8 — 5 можно считать сокращенной записью суммы (+ 8) + (— 5) или, что то же самое, суммы 8 + (— 5). Аналогично выражение
можно считать сокращенной записью суммы
Ввиду того что в алгебре разность можно рассматривать как сумму, выражения 8 — 5, 8 — 5+12 — 4 и им подобные называются алгебраическими суммами.
обозначает сумму следующих слагаемых: 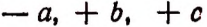
Точно так же выражение
обозначает сумму следующих выражений:
Изложенное можно сформулировать следующим образом. Несколько алгебраических выражений, соединенных знаками + или —, можно рассматривать как сумму. Имея это в виду, совокупность алгебраических выражений, соединенных между собой знаками + или —, называют алгебраической суммой.
суть алгебраические суммы.
Слагаемыми алгебраической суммы а — b будут а и — b ; слагаемыми алгебраической суммы 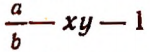
Слагаемые алгебраической суммы называются ее членами.
Каждая алгебраическая сумма является в то же время и многочленным выражением. Члены алгебраической суммы называются одновременно и членами многочлена.
Обратно, каждый многочлен является в то же время и алгебраической суммой.
Пример:
Алгебраическая сумма обладает всеми свойствами суммы, перечисленными в § 4 главы I.
На основании изложенного выше мы можем вместо выражения