Что называют числовой функцией

Числовая функция

В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел или множества комплексных чисел .

Содержание

График функции

Примеры

Способы задания функции

Словесный	С помощью естественного языка	Игрек равно целая часть от икс.
Аналитический	С помощью формулы и стандартных обозначений
Графический	С помощью графика
Табличный	С помощью таблицы значений	x 0 1 2 3 4 5 6 7 8 9 y 1 1 2 3 5 8 13 21 34 55

Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента.

Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:

Графический способ

Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.

Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

Словесный способ

Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.

Классы числовых функций

Исторический очерк

Появление понятия

Математический термин «функция» впервые появился в 1673 году у Лейбница, и притом не совсем в современном его понимании: Лейбниц вначале называл функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). Позже, однако, в переписке с Иоганном Бернулли (1694) содержание термина расширяется и в конце концов становится синонимом «аналитически заданной зависимости».

В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.

Первые попытки определения

В начале XVIII века были получены разложения всех стандартных функций и многих других. Благодаря, в основном, Эйлеру (1748) были уточнены их определения. Эйлер впервые ясно определил показательную функцию, а также логарифмическую как обратную к ней, и дал их разложения в ряд. До Эйлера многие математики считали, например, тангенс тупого угла положительным; Эйлер дал современные определения всех тригонометрических функций (сам термин «тригонометрическая функция» предложил Клюгель в 1770 году).

В приложениях анализа появляется множество новых трансцендентных функций. Когда Гольдбах и Бернулли попытались найти непрерывный аналог факториала, молодой Эйлер сообщил в письме Гольдбаху о свойствах гамма-функции (1729, название принадлежит Лежандру). Через год Эйлер открыл бета-функцию, и далее неоднократно возвращался к этой теме. Гамма-функция и связанные с ней (бета, дзета, цилиндрические (Бесселя)) находят многочисленные применения в анализе, а также в теории чисел, а дзета-функция Римана оказалась незаменимым инструментом для изучения распределения простых чисел в натуральном ряду.

В 1757 году Винченцо Риккати, исследуя секторы гиперболы, вводит гиперболические функции ch, sh (именно с такими обозначениями) и перечисляет их основные свойства. Немало новых функций возникло в связи с неинтегрируемостью различных выражений. Эйлер определил (1768) интегральный логарифм (название предложил И. Зольднер, 1809), Л. Маскерони — интегральные синус и косинус (1790). Вскоре появляется и новый раздел математики: специальные функции.

С этим пёстрым собранием надо было что-то делать, и математики приняли радикальное решение: все функции, независимо от их происхождения, были объявлены равноправными. Единственное требование, предъявляемое к функции — определённость, причём имеется в виду не однозначность самой функции (она может быть и многозначной), а недвусмысленность способа вычисления её значений.

Первое общее определение функции встречается у Иоганна Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств».

Всё же в XVIII веке отсутствовало достаточно ясное понимание различия между функцией и её аналитическим выражением. Это нашло отражение в той критике, которой Эйлер подверг решение задачи о колебании струны, предложенное Бернулли (1753). В основе решения Бернулли лежало утверждение о возможности разложить любую функцию в тригонометрический ряд. Возражая против этого, Эйлер указал на то, что подобная разложимость доставляла бы для любой функции аналитическое выражение, в то время как функция может и не иметь его (она может быть задана графиком, «начертанным свободным движением руки»).

Под влиянием теории бесконечных рядов, которые давали алгебраическое представление почти любой гладкой зависимости, наличие явной формулы постепенно перестало быть обязательным для функции. Логарифм или показательная функция, например, вычисляются как пределы бесконечных рядов; такой подход распространился и на другие нестандартные функции. С рядами стали обращаться как с конечными выражениями, первоначально никак не обосновывая корректность операций и даже не гарантируя сходимость ряда.

Начиная с «Дифференциального исчисления» (1755), Эйлер фактически принимает современное определение числовой функции как произвольного соответствия чисел [3] :

Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых.

Общее определение

В «Аналитической теории тепла» Фурье (1822) имеется фраза: «Функция обозначает функцию совершенно произвольную, то есть последовательность данных значений, подчинённых или нет общему закону и соответствующих всем значениям , содержащимся между и какой-либо величиной ».

Близко к современному и определение Лобачевского:

…Общее понятие функции требует, чтобы функцией от называть число, которое даётся для каждого и вместе с постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной… Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе.

Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое Дирихле, неоднократно предлагалось и до него. Вот определение Дирихле (1837):

у есть функция переменной х (на отрезке ), если каждому значению х (на этом отрезке) соответствует совершенно определённое значение у, причем безразлично, каким образом установлено это соответствие — аналитической формулой, графиком, таблицей, либо даже просто словами.

К концу XIX века понятие функции перерастает рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.

Примеры

Неявные функции

Функции могут быть заданы при помощи других функций и уравнений.

Предположим, задана функция двух переменных, которая удовлетворяет специальным условиям (условиям теоремы о неявных функций), тогда уравнение вида.

.

определяет неявную функцию вида .

Источник

Числовые функции

Понятие числовой функции.

Пусть дано числовое множество \(X\subset\mathbb\). Если каждому \(x\in X\) поставлено в соответствие по некоторому правилу число \(y\). то говорят, что на множестве \(X\) определена числовая функция.

Правило, устанавливающее соответствие, обозначают некоторым символом, например, \(f\) и пишут
$$
y=f(x),\;x\in X,\label
$$
а множество \(X\) называют областью определения функции и обозначают \(D(f)\), то есть \(X=D(f)\).

\(x\) часто называют аргументом или независимой переменной, а \(y\) — зависимой переменной. Числа \(x\) из множества \(D(f)\) называют значениями аргумента. Число \(y_0\), соответствующее значению \(x_<0>\in D(f)\), называют значением функции при \(x=x_<0>\) (или значением функции в точке \(x_0\)) и обозначают \(f(x_0)\) или \(f(x)|_>\). Совокупность всех значений, которые функция принимает на множестве \(D(f)\), называют множеством значений функции и обозначают \(E(f)\). Заметим, что если \(y_0\in E(f)\), то существует по крайней мере одно число \(x_<0>\in D(f)\) такое, что \(f(x_0)=y_0\).

Функцию часто обозначают только символом (\(f,\;\varphi,\;F\) и т. д.), который определяет правило (закон) соответствия. Для обозначения функции используются также записи вида \(x\mapsto f(x),\;f:\;X\rightarrow Y\). Под словом «функция» часто понимают зависимую переменную \(у\), значения которой определяются значениями независимой переменной \(x\) и правилом \(f\), или даже само это правило. Термин «функция» имеет синонимы: отображение, преобразование, морфизм. Например, говорят, что функция \(f\) отображает множество \(X=D(f)\) на множество \(Y=E(f)\), и называют множество \(Y\) образом множества \(X\) при отображении \(f\). Если \(E(f)\subset E_1\), то говорят, что функция \(f\) отображает \(X\) в \(E_1\).

Равенство функций. Операции над функциями.

Функции \(f\) и \(g\) называют равными или совпадающими, если они имеют одну и ту же область определения \(X\) и для каждого \(x\in X\) значения этих функций совпадают. В этом случае пишут \(f(x)=g(x),\ x\in X\) или \(f=g\).

Например, если \(f(x)=\sqrt>, \ x\in\mathbb\),и \(g(x)=|x|, \ x\in\mathbb\), то \(f=g\), так как при всех \(x\in\mathbb\) справедливо равенство \(\sqrt>=|x|\).

Если равенство \(f(x)=g(x)\) верно при всех \(x\in E’\), где \(E’\subset D(f)\cap D(g)\), то есть сужения функций f и g на множество \(E’\) совпадают, то в этом случае говорят, что функции \(f\) и \(g\) равны на множестве \(E’\). Например, функции \(\sqrt>\) и \(x\) равны на множестве \( E’=[0,+\infty\)).

Способы задания функции.

Числовые функции чаще всего задаются при помощи формул. Такой способ задания называют аналитическим. Например, функции \(y=x^2, \ y=|x|^<3>, \ y=\sin^3<3x>\) заданы на множестве \(\mathbb\) аналитически.

Следует отметить, что функция может быть задана различными формулами на разных промежутках. Например, функция
$$
f(x)=\left\<\begin-x,\quad если\;x\; 1,\end\right.\nonumber
$$
задана аналитическим способом на \(\mathbb\) с помощью трех различных формул.

Иногда функциональная зависимость описывается с помощью таблицы, содержащей лишь некоторые значения аргумента и соответствующие значения функции. Для значений аргумента, не содержащихся в таблице, значения функции обычно находят приближенно.

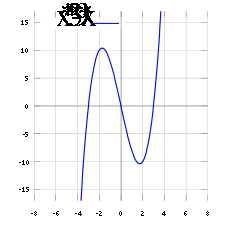
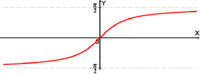
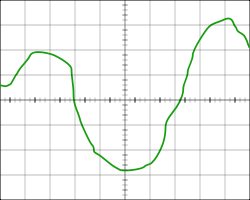
На практике часто соответствие между значениями аргумента и значениями функции задается с помощью рисунка. Например, в медицине при изучении работы сердца получают электрокардиограммы — кривые, отражающие изменение с течением времени электрических импульсов в мышце сердца. В практике физических измерений функциональная зависимость часто задается с помощью эскиза графика, снимаемого, например, с экрана осциллографа.

График функции.

Графиком функции \(y=f(x), x\in D(f),\) в прямоугольной системе координат \(Oxy\)-называют множество всех точек плоскости с координатами \((x,f(x)\overline<)>\), где \(x\in D(f)\).

Строго говоря, следует различать график функции, точное определение которого дано выше, и эскиз части графика, принимаемый нередко за график.

Пусть \(x\in[n,n+1\)), где \(n\in Z\), тогда \(E(x)=n\). График функции \(y=E(z)\) изображен на рис. 9.1. Стрелка на графике указывает на то, что точка в ее острие не принадлежит графику.

Рис. 9.1

Построить график функции \(y=sign\;\sin x\) где
$$
\operatorname\;x=\left\<\begin1,\quad если\quad x>0,\\0,\quad если\quad x=0,\\-1,\quad если\quad x\; Решение

Рис. 9.2

График функции \(y=f(x)\) иногда можно получить преобразованием известного графика другой функции \(y=g(x)\).

Приведем примеры применения преобразований, указанных в таблице.

График квадратичной функции
$$
y=ax^<2>+bx+c,\quad a\neq 0,\label
$$
можно получить сдвигом графика функции \(у=ах\) вдоль оси \(Ox\).

\(\triangle\) Действительно, выделяя полный квадрат, получаем
$$
ax^2+bx+c=a(x+\displaystyle \frac<2a>)^<2>+c-\frac><4a>.\nonumber
$$
Поэтому графиком квадратичной функции \eqref является парабола, получаемая сдвигом параболы \(y=ax^<2>.\quad\blacktriangle\)

Рис. 9.3

График дробно-линейной функции
$$
y=\displaystyle \frac,\quad c\neq 0,\quad ad-bc\neq 0,\label
$$
можно получить преобразованием графика функции вида \(y=\displaystyle \frac\).

В частности, если \(y=\displaystyle \frac<3-2x>\), то \(y=\displaystyle \frac<5-2(x+1)>=-2+\frac<5>\).

Рис. 9.4

Построить график функции \(y=\sqrt<-x>\).

\(\triangle\) График функции \(y=\sqrt<-x>\) можно получить из графика функции \(y=\sqrt\) с помощью симметрии относительно оси ординат (рис. 9.5).\(\blacktriangle\)

Отметим еще, что график функции \(y=|f(x)|\) можно получить из графика функции \(у=f(x)\) следующим образом:

Построить график функции \(y=|x^<2>-2x|.\)

\(\triangle\) Применяя указанный выше прием, строим график этой функции (рис. 9.6) с помощью графика функции \(y=x^<2>-2x\) (рис.9.3). \(\blacktriangle\)

Четные и нечетные функции.

Функция f, определенная на множестве X, называется:

Четными являются, например, следующие функции: \(\displaystyle y=x^<4>,\;y=\cos\frac<2>,\;y=\lg |x|,\;y=\frac<\sin x>\), а нечетными — функции \(y=\displaystyle \frac<1>>,\ y=\sin^<5>2x, y=x^<2>\displaystyle \operatorname\frac<2>,\ y=\arcsin(\sin x)\).

График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

Построить график функции \(y=x^<2>-2|x|.\)

\(\triangle\) Если \(x\geq 0,\) то \(y =x^2-2x\) (см. рис. 9.3). Так как \(x^<2>-2|x|\)— четная функция, то для функции, соответствующей значениям \(x\leq 0\), следует симметрично отразить график \(y=x^<2>-2x, x\geq 0,\) относительно оси \(Oy\) (рис. 9.7). \(\blacktriangle\)

На рис. 9.8 изображен график нечетной функции \(y=x^<3>.\)

Рис. 9.8

Ограниченные и неограниченные функции.

Функцию f называют ограниченной снизу на множестве \(X\subset D(f)\), если существует число \(С_1\) такое, что для любого \(x\in X\) выполняется неравенство \(f(x) \geq C_1\).

Используя символы \(\exists\) и \(\forall\), это определение можно записать так:
$$
\exists C_<1>:\forall x\in X\rightarrow f(x)\geq C_<1>.\nonumber
$$
Аналогично функцию f называют ограниченной сверху на множестве \(X\subset D(f)\), если
$$
\exists C_<2>:\forall x\in X\rightarrow f(x)\leq C_<2>.\nonumber
$$

Функцию, ограниченную и сверху, и снизу на множестве X, называют ограниченной на этом множестве.

Функция f является ограниченной на множестве X тогда и только тогда, когда
$$
\exists c>0:\forall x\in X\rightarrow|f(x)|\leq C.\label
$$

Если неравенство \(|f(x)|\leq C\) выполняется для всех \(x\in D(f)\), говорят, что функция f ограничена.

Геометрически ограниченность функции f на множестве X означает, что график функции \(y=f(x), x\in X,\) лежит в полосе \(<-C\leq y\leq C>.\)

Например, функция \(y=\displaystyle \sin\frac<1>\), определенная при \(x\in\mathbb, x\neq 0\), ограничена, так как
$$
|\sin\frac<1>|\leq 1\nonumber
$$

Функция f не ограничена на множестве X, если условие \eqref не выполняется, то есть
$$
\forall C>0\ \exists x_\in X:|f(x_)|\geq C.\label
$$

Если \(X= D(f)\) и выполнено условие \eqref, то говорят, что функция f не ограничена.

Доказать, что функция \(y=\displaystyle \frac<1>>\) не ограничена.

\(\triangle\) Функция \(\displaystyle \frac<1>>\) определена при \(x\in\mathbb\), \(x\neq 0\). Пусть C — любое положительное число, и пусть \(\displaystyle =\frac<1><\sqrt<2C>>>\), тогда \(\displaystyle y(x_)=2C>C\) то есть выполняется условие \eqref. \(\blacktriangle\)

Пусть существует точка \(x_<0>\in X\subset D(f)\) такая, что для всех \(x\in X\) выполняется неравенстве \(f(x) \leq f(x_0)\).Тогда говорят, что функция f принимает в точке \(x_<0>\) наибольшее (максимальное) значение на множестве X и пишут \(f(x_<0>)=\displaystyle \max_f(x)\) В этом случае \(\displaystyle \sup_=f(x_<0>) \)

Максимальные и минимальные значения называют экстремальными.

Монотонные функции.

Функцию \(f\) называют возрастающей (неубывающей) на множестве \(X\subset D(f)\), если для любых точек \(x_1 \in X, x_<2>\in X\) таких, что \(x_<1>\; f(x_<2>).\nonumber
$$

Убывающие и возрастающие функции объединяют названием монотонные, а строго возрастающие и строго убывающие — названием строго монотонные.

Если \(X=D(f)\), то в этих определениях указание на множество \(X\) обычно опускают.

Доказать, что функция f строго возрастает на множестве X, если:

Источник