Что называют биссектрисой угла 7 класс

Угол. Биссектриса. Виды углов.

теория по математике 📈 планиметрия

Угол – геометрическая фигура, состоящая из точки и двух лучей, которые исходят из этой точки. Лучи – стороны угла, а точка – вершина.

Обозначение углов: можно обозначать тремя заглавными латинскими буквами (в середине записи – буква, которая обозначает вершину угла); можно обозначать одной заглавной латинской буквой; также используется обозначение двумя прописными латинскими буквами.

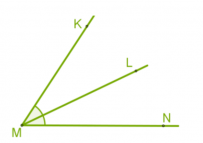
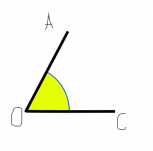
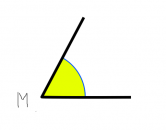
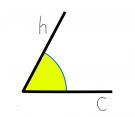
Рассмотрим обозначение на рисунках, где на рисунке 1 показан угол АОС, на рисунке 2 – угол М, на рисунке 3 – угол (hc).

Рисунок 1	Рисунок 2	Рисунок 3

Измерение углов. Виды углов

Обычно за единицу измерения углов принимают градус – угол, равный одной стовосьмидесятой части развернутого угла. Эта единица измерения введена до нашей эры много веков назад и используется в наше время.

Число, которое указывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла.

Определенные части градуса носят такие названия, как минута и секунда, где минута – это 1/60 часть угла, а секунда – это 1/60 часть минуты.

Запись и чтение осуществляется следующим образом: 78 0 (78 градусов); 24 0 32 / 45 // — это 24 градуса 32 минуты 45 секунд. Определение

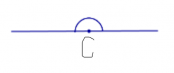
Угол называется развернутым, если обе его стороны лежат на одной прямой.

Также можно сказать, что одна сторона развернутого угла является продолжением другой стороны этого угла. На рисунке показан развернутый угол С. Его величина равна 180 градусам (180 0 ).

Определение

Угол, градусная мера которого равна 90 градусов, называется – прямой.

Биссектриса угла

Биссектрисой угла называется луч, исходящий из вершины и делящий его на два равных угла. На рисунке показан луч ML, который делит угол KMN пополам, то есть угол KML равен углу LMN.

Смежные углы

Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.

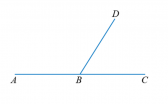
На рисунке показаны углы ABD и DBC, которые являются смежными, у них сторона BD общая, а стороны АВ и ВС являются продолжениями одна другой.

По рисунку мы видим, что эти два смежных угла образуют развернутый угол. Таким образом, сумма смежных углов равна 180 градусов. Это свойство смежных углов.

Смежные углы

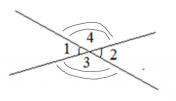
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла. Другими словами, при пересечении двух прямых образуются две пары вертикальных углов.

На рисунке показаны две пары вертикальных углов, это пара углов 1 и 2, а также вторая пара – это 3 и 4.

Источник

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Источник

Биссектриса угла, биссектриса треугольника: что это такое и в чем разница

Биссектриса угла – луч, исходящий из вершины угла и разделяющий его пополам.

Биссектриса треугольника – отрезок, проведенный от вершины угла до противолежащей стороны треугольника.

В треугольнике может быть только три (внутренних) биссектрисы, каждая из которых будет делить свою вершину на два равных угла.

Что означает слово «биссектриса»?

«Биссектриса» – слово латинского происхождения, состоящее из двух частей: «bi» – «пара, двойное» и «sectio» – «разрезать, делить».

Название отражает суть: деление чего-то пополам, то есть на две равные части. В случае биссектрисы в роли «чего-то» выступает угол, который она делит на два угла.

Если при упоминании биссектрисы вам на ум приходит «крыса, бегающая по углам и делящая их пополам» из известного двустишия, то в принципе это не будет ошибкой ее определения, с той лишь поправкой, что каждая такая «крыса» должна замереть в конкретном положении для заданного угла, чтобы каждая ее точка была равноудалена от сторон этого угла.

Свойства биссектрисы

Есть несколько качеств биссектрисы, по которым ее легко узнать или вычислить.

В любом треугольнике все три биссектрисы всегда будут пересекаться в одной и той же точке.

Точка пересечения биссектрис в треугольнике является центром вписанной в этот треугольник окружности.

В равнобедренном треугольнике биссектриса совпадает с медианой и высотой.

В равностороннем треугольнике (это равнобедренный треугольник с равными углами) все три биссектрисы являются высотами и медианами. Кроме того, все они – три биссектрисы, медианы и высоты – будут одной и той же длины.

И последнее по счету (но не по значению) свойство биссектрисы. Зная его, вы сможете решить большинство задач по геометрии, где нужно вычислить длины сторон треугольника.

Биссектриса делит противоположную своему углу сторону треугольника на два отрезка. И отношение длин этих отрезков (записывается в виде дроби) в точности равно отношению двух соседних сторон всего треугольника.

Применение биссектрисы на практике

Биссектриса не является лишь абстрактным математическим понятием. На самом деле без знания этого термина и его сути невозможно обойтись во многих сферах: при строительстве крыши, при защите радиовысотомеров от радиолокационных ракет, при конструировании кораблей, при исследовании следов орудий взлома и так далее.

Источник

Что называют биссектрисой угла 7 класс

СОДЕРЖАНИЕ: 7) Равные треугольники. Высота, медиана, биссектриса треугольника. 8) Первый и второй признак равенства треугольников. 9) Равнобедренный треугольник и его свойства. 10) Признаки равнобедренного треугольника. 11) Третий признак равенства треугольников. 12) Теоремы.

§ 7. Равные треугольники. Высота, медиана, биссектриса треугольника

Рассмотрим три точки А, В, С, не лежащие на одной прямой. Соединим их отрезками АВ, ВС, СА. Полученная фигура ограничивает часть плоскости, выделенную на рисунке 108 зеленым цветом. Эту часть плоскости вместе с отрезками АВ, ВС и СА называют треугольником.

Точки А, В, С называют вершинами, а отрезки АВ, ВС, СА — сторонами треугольника. Треугольник называют и обозначают по его вершинам. Треугольник, изображённый на рисунке 108, обозначают так: ΔАВС, или ΔВСА, или ΔАСВ (читают: «треугольник АВС», «треугольник ВСА», «треугольник АСВ»).

§ 8. Первый и второй признак равенства треугольников

§ 9. Равнобедренный треугольник и его свойства

Определение. Треугольник, у которого две стороны равны, называют равнобедренным.
Равные стороны треугольника называют боковыми сторонами, а третью сторону — основанием равнобедренного треугольника. Вершиной равнобедренного треугольника называют общую точку его боковых сторон. При этом угол В называют углом при вершине, а углы А и С — углами при основании равнобедренного треугольника.

Определение. Треугольник, у которого все стороны равны, называют равносторонним.
Равносторонний треугольник — частный случай равнобедренного треугольника.

§ 10. Признаки равнобедренного треугольника

§ 11. Третий признак равенства треугольников

§ 12. Теоремы

Формулировки всех теорем, которые мы доказали, состоят из двух частей. Первую часть теоремы (то, что дано) называют условием теоремы, вторую часть теоремы (то, что требуется доказать) — заключением.

Например, в теореме 8.1 (первый признак равенства треугольников) условием является то, что две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, а заключением — равенство
ников.

Все знакомые вам теоремы можно условно разделить на теоремы-свойства и теоремы-признаки. Например, теорема 1.1 устанавливает свойство пересекающихся прямых, теорема 9.1 — свойство равнобедренного треугольника.

Теоремы-признаки перечисляют свойства, по которым можно распознать фигуру, т. е. отнести её к тому или иному виду (классу). Так, теоремы-признаки равенства треугольников указывают требования, по которым два треугольника можно причислить к классу равных. Например, в теоремах 10.1-10.4 сформулированы свойства, по которым распознают равнобедренный треугольник.

Теоремы, которые следуют непосредственно из аксиом или теорем, называют теоремами-следствиями или следствиями. Например, свойство углов, противолежащих равным сторонам треугольника, является следствием из теоремы 9.1.
Если в теореме 8.2 о свойстве серединного перпендикуляра поменять местами условие и заключение, то получим теорему 11.2. Такие теоремы называют взаимно обратными. Если какую-то из этих теорем назвать прямой, то вторую теорему будем называть обратной.

Меняя местами условие и заключение теоремы, надо быть очень внимательными: не всегда можно получить истинное утверждение. Например, утверждение, обратное теореме 4.1 о сумме смежных углов, неверно. Действительно, если сумма каких-то двух углов равна 180°, то совершенно не обязательно, чтобы эти углы были смежными.

Вы знаете, что справедливость теоремы устанавливают путём логических рассуждений, т. е. доказательства. Теорема 1.1 была доказана методом от противного. Название этого метода фактически отражает его суть. Мы предположили, что заключение теоремы 1.1 неверно. На основании этого предположения с помощью логических рассуждений был получен факт, который противоречил основному свойству прямой.

Методом от противного также были доказаны и другие теоремы, например теоремы 5.1, 10.3. Очень важно, чтобы доказательство теоремы было полным, т. е. рассмотрены все возможные случаи. Так, полное доказательство теоремы 11.1 (третий признак равенства треугольников) потребовало рассмотрения всех трёх возможных случаев.

Умение видеть все тонкости и нюансы доказательства — важнейшее качество, формирующее математическую культуру. Если бы, например, при доказательстве теоремы 8.2 о свойстве серединного перпендикуляра мы не рассмотрели отдельно случай, когда точка X является серединой отрезка то обращение к треугольникам АХМ и ВХМ было бы не совсем «законным».

При доказательстве теоремы 10.4 (признак равнобедренного треугольника) мы использовали приём дополнительного построения: чертёж дополнили элементами, о которых не шла речь в условии теоремы. Этот метод является ключом к решению многих задач и доказательству ряда теорем. Поэтому очень важно научиться видеть «выгодное» (результативное) дополнительное построение.

ИТОГИ ГЛАВЫ 2.

Определение. Равные фигуры
Две фигуры называют равными, если их можно совместить наложением.

Основное свойство равенства треугольников
Для данного треугольника АВС и луча А₁М существует треугольник A₁B₁C₁ равный треугольнику АВС, такой, что АВ = А₁В₁, ВС = В₁С₁, АС = А₁С₁ и сторона A₁B₁ принадлежит лучу А₁М, а вершина С₁ лежит в заданной полуплоскости относительно прямой А₁М.

ТЕОРЕМА 7.1. О единственности прямой, перпендикулярной данной
Через точку, не принадлежащую данной прямой, проходит только одна прямая, перпендикулярная данной.

Высота треугольника
Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону, называют высотой треугольника.

Медиана треугольника
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называют медианой треугольника.

Биссектриса треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называют биссектрисой треугольника.

ТЕОРЕМА 8.1. Первый признак равенства треугольников: по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Серединный перпендикуляр отрезка
Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.

ТЕОРЕМА 8.2.
Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.

ТЕОРЕМА 8.3. Второй признак равенства треугольников: по стороне и двум прилежащим к ней углам
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Равнобедренный треугольник
Треугольник, у которого две стороны равны, называют равнобедренным.

Равносторонний треугольник
Треугольник, у которого все стороны равны, называют равносторонним.

ТЕОРЕМА 9.1. Свойства равнобедренного треугольника
В равнобедренном треугольнике: 1) углы при основании равны; 2) биссектриса треугольника, проведённая из угла при вершине, является медианой и высотой.

Свойства треугольников, следующие из свойств равнобедренного треугольника
• В треугольнике против равных сторон лежат равные углы.
• В равнобедренном треугольнике биссектриса, высота и медиана, проведённые из его вершины, совпадают.
• В равностороннем треугольнике все углы равны.
• В равностороннем треугольнике биссектриса, высота и медиана, проведённые из одной вершины, совпадают.

Признаки равнобедренного треугольника
• Если медиана треугольника является его высотой, то этот треугольник равнобедренный (Теорема 10.1)
• Если биссектриса треугольника является его высотой, то этот треугольник равнобедренный (Теорема 10.2)
• Если в треугольнике два угла равны, то этот треугольник равнобедренный (Теорема 10.3)
• Если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный (Теорема 10.4)

ТЕОРЕМА 11.1.Третий признак равенства треугольников: по трём сторонам
Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны.

Это конспект по теме «Мерзляк Геометрия 7 Глава 2». Выберите дальнейшие действия:

Источник

Урок по геометрии на тему «Биссектриса угла»( 7 класс)

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Тема: «Биссектриса угла»

Цели задачи : ввести понятие биссектрисы угла, рассмотреть решение задач на определение углов между пересекающимися прямыми; рассмотреть решение задач с применением биссектрисы; развивать пространственное воображение и представление учащихся, культуру чертежа и оформления геометрической задачи, воспитывать интерес к предмету.

Тип урока: объяснение нового материала

Оборудование : чертежные инструменты

2.Проверка домашнего задания: с.19 ПЗ

-Дайте определение угла.

-Какие виды углов вы знаете?

Сколько минут в 1 градусе?

Расстояние между населенными пунктами обычно измеряют в …?

Что мы делаем с углами с помощью транспортира?

— Что такое биссектриса?

Так ответил на вопрос:

-Это луч, который нам

Делит угол пополам.

Он выходит на века

Биссектриса угла- это луч с началом в вершине угла, делящий угол на два равных угла.

Выполним чертеж в тетради.

Посмотрим на рисунки является ли луч биссектрисой угла?

Для этого существуют способы построения биссектрисы угла.

Перегиб модели угла

С помощью транспортира

С помощью циркуля и линейки.

Перегиб модели. Показать перегиб из разных материалов.

Вспомним как мы строили углы в 5 классе.

Алгоритм измерения углов

Совместить вершину угла с отметкой Центром на транспортире.

-Один из лучей совместить с нулевой отметкой на транспортире

-Посмотреть через какую отметку проходит другой луч, и назвать градусную меру угла.

— сколько градусов этот угол?

Если бы мы провели биссектрису этого угла, то она разделила этот угол на 2 равных угла? Какие углы у нас получились?

4. Решение задач по готовым чертежам.

Определить градусную меру угла АОС. будет ли луч ОВ биссектрисой угла АОС.

Устно решение задач

— Чему равен угол между биссектрисой и стороной данного угла, если угол равен 60, 52, 160.

-Найдите угол, если его биссектриса образует со стороной угол, равный 50, 75, 64.

5. Подведение итогов.

Что такое биссектриса угла?

Способы построения угла?

6. Домашнее задание:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-248580

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Международный конгресс-выставка «Молодые профессионалы» пройдет с 12 по 14 декабря в Москве

Время чтения: 1 минута

Школьники из Москвы выступят на Международной олимпиаде мегаполисов

Время чтения: 3 минуты

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Госдума приняла закон об использовании онлайн-ресурсов в школах

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник