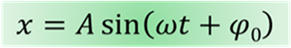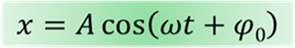Что называют амплитудой гармонических колебаний
Амплитуда, период, частота колебаний.
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
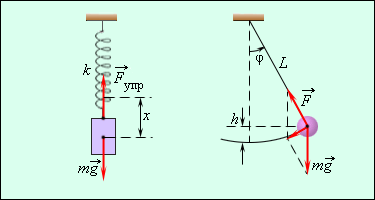
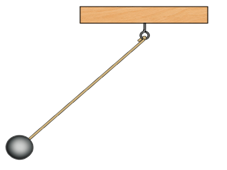
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
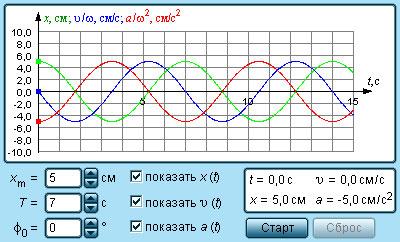
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
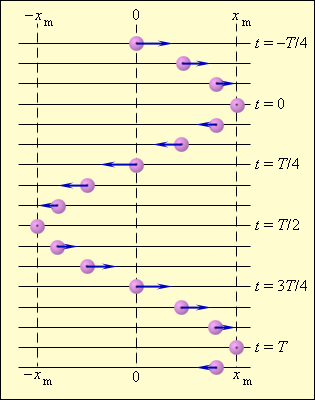
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.
За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
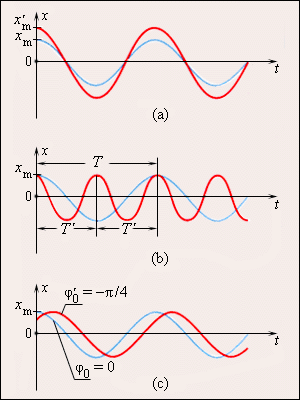
Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, т. е. для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Гармонические колебания
Техника и окружающий мир являются примерами того, что существуют такие процессы, которые повторяются через определенные промежутки времени, то есть периодически. Их называют колебательными.
Колебательные движения. Формулы
Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.
Механические колебания – это периодические или непериодические изменения физической величины, описывающей механическое движение (скорость, перемещение и так далее).
Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке. Так возникают механические волны. Явный пример – звуковые волны в воздухе.
Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.
Гармонические колебания. Определение
В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.
Механические колебания – это движения тел, которые повторяются точно или приблизительно за определенные одинаковые временные промежутки.
Механические колебания подразделяют на свободные и вынужденные.
Действия внутренних сил системы после выведения из равновесия порождают свободные колебания. Примером могут служить колебания груза на пружине или маятника. Если их действие происходит под воздействием внешних сил, тогда их называют вынужденными.
Гармонический закон
Гармонические колебания. Амплитуда, период и частота колебательного движения
Урок 24. Физика 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Гармонические колебания. Амплитуда, период и частота колебательного движения»
В рамках прошлой темы говорилось о новом виде механического движения – колебательном движении.
Механическое колебательное движение —это движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях.
Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.
Колебательной системой называют такую физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания.
Маятник – это твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
В рамках данной темы будет рассмотрен простейший вид колебательного движения — гармонические колебания.
Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
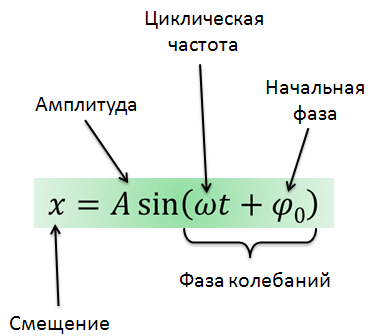
Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:
Эти уравнения называют кинематическим законом гармонического движения.
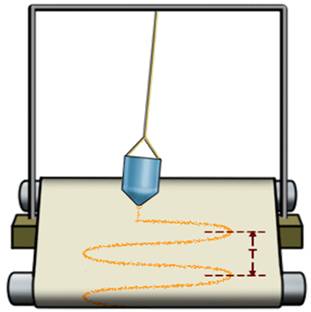
Покажем, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую установку.
Возьмем нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с маленьким отверстием снизу и насыплем в него песок.А под полученную систему положим длинную бумажную ленту.
Если ленту перемещать с постоянной скоростью в направлении, перпендикулярном плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая точка которой соответствует положению колеблющегося груза в тот момент, когда он проходил над ней. Из опыта видно, что след, который оставляет песок на листе бумаги, есть некая кривая.
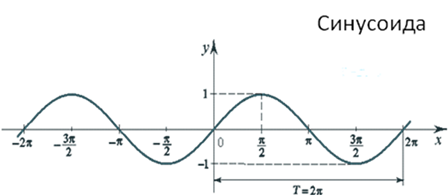
Она называется синусоидой. Из курса математики старших классов вы узнаете о том, что аналогичные графики имеют функции типа
Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.
Через точки, соответствующие положению равновесия маятника, проведена ось времени t, а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно определить координату груза в любой момент времени.
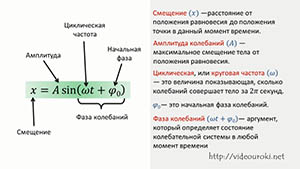
Теперь разберемся с величинами, входящими в уравнение колебательного движения.
Смещение — величина, характеризующая положение колеблющейся точки в некоторый момент времени относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в данный момент времени.
Амплитуда колебаний — максимальное смещение тела от положения равновесия.
Циклическая, или круговая частота, показывающая, сколько колебаний совершает тело за 2p секунд.
j0 — это начальная фаза колебаний.
Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Период колебаний обычно обозначается буквой Т и в системе СИ измеряется в секундах.
Число колебаний в единицу времени называется частотой колебаний. Обозначается частота буквой ν. За единицу частоты принято одно колебание в секунду. Эта единица названа в честь немецкого ученого Генриха Герца.
Период колебания и частота колебаний связаны следующей зависимостью:
Т.е. частота — это величина обратная периоду и равная числу полных колебаний, совершаемых за 1 секунду.
Циклическая частота также связана с периодом колебаний или частотой. Эту связь математически можно записать в следующем виде:
Таким образом, любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
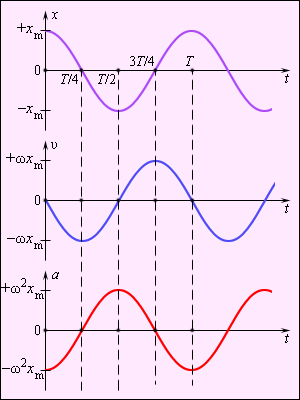
При совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или косинуса.
Это следует из известных вам законов и формул, в которых указанные величины попарно связаны прямо пропорциональной зависимостью, например законом Гука или вторым законом Ньютона. Из этих формул видно, что сила и ускорение достигают наибольших значений, когда колеблющееся тело находится в крайних положениях, где смещение наиболее велико, и равны нулю, когда тело проходит через положение равновесия.
Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.
Колебания, практически близкие к гармоническим, совершает тяжелый шарик, подвешенный на легкой и малорастяжимой нити, длина которой значительно больше диаметра шарика. Такую колебательную систему называют математическим маятником.
Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
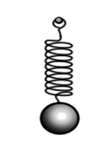
Также гармонические колебания может совершать груз подвешенный на пружине, совершающий колебания в вертикальной плоскости. Такую колебательную систему называют пружинным маятником — это система, состоящая из материальной точки массой m и пружины.
– Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
– Любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
– Амплитуда колебаний — максимальное смещение тела от положения равновесия.
– Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
– Число колебаний в единицу времени называется частотой колебаний.
– Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
– Математический и пружинный маятники — это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса или косинуса.
– Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
– Пружинный маятник — это система, состоящая из материальной точки массой m и пружины, которая совершает колебания в вертикальной плоскости.
Амплитуда гармонических колебаний
Вы будете перенаправлены на Автор24
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени. Эти движения мы можем наблюдать:
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Данный тип колебаний применяют:
Колебания, которые происходят под воздействием сил внутри самой колебательной системы, называют собственными. Собственные колебания появляются при нарушении состояния равновесия колебательной системы.
Гармоническими называют колебания, которые описывают при помощи тригонометрических законов синуса и косинуса.
Уравнение собственных электрических колебаний
Допустим, что электрические процессы в контуре, состоящем из:
являются квазистационарными. Это означает:
Изменение заряда описывает в таком контуре дифференциальное уравнение второго порядка с обыкновенными производными и постоянными коэффициентами:
Аналогичные уравнения описывают колебания напряжения и силы тока.
Если колебания описываю при помощи линейных дифференциальных уравнений, то такие колебания являются линейными, соответствующие им колебательные системы, именуют линейными колебательными системами.
Готовые работы на аналогичную тему
Амплитуды заряда, силы тока и напряжения при колебаниях в идеальном электрическом контуре.
Для того чтобы задача описания колебаний стала полностью определенной необходимо задать начальные условия, которых должно быть два, так как мы имеем уравнение второго порядка. Обычно начальными условиями для уравнения (1) являются:
Если сопротивление контура можно считать равным нулю ($R=0$), тогда уравнение колебаний (1) принимает вид:
Общим решением уравнения (2) является гармоническое колебание:
$q=A\cos (\omega_0 t+\varphi) (3),$
Амплитуда (как и начальная фаза) определяются начальными условиями колебаний.
Подставим начальные условия в гармоническое колебание (3), получим:
В окончательном виде уравнение гармонического колебания (3) запишем как:
$q=q_0\cos (\omega_0 t) (4).$
Напряжение на конденсаторе в контуре изменяется в соответствии с законом:
$U_C=\frac
Силу тока в контуре найдём как:
$I=-\frac
Поскольку из тригонометрии мы знаем, что:
Амплитуда гармонических механических колебаниях
$x=A\cos (\omega t+\delta)(7),$
$v=\dot
Найдем вторую производную от уравнения колебаний (7), имеем:
Амплитуда колебаний при наличии затухания
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 22 05 2021
Что называют амплитудой гармонических колебаний
Ускорение — вторая производная координаты по времени.
где х» — вторая производная координаты по времени.
При свободных колебаниях координата х изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
Гармонические колебания
Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями.
Амплитуда колебаний
Амплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия.
Амплитуда определяется начальными условиями, а точнее энергией, сообщаемой телу.
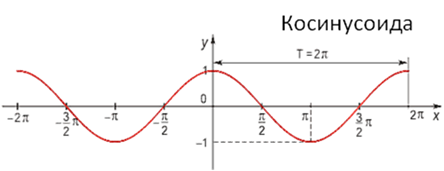
График зависимости координаты тела от времени представляет собой косинусоиду.
Тогда уравнение движения, описывающее свободные колебания маятника:
Период и частота гармонических колебаний.
При колебаниях движения тела периодически повторяются.
Промежуток времени Т, за который система совершает один полный цикл колебаний, называется периодом колебаний.
В Международной системе единиц (СИ) единица частоты называется герцем (Гц) в честь немецкого физика Г. Герца.
Число колебаний за 2π с равно:
Величина ω0 — это циклическая (или круговая) частота колебаний.
Через промежуток времени, равный одному периоду, колебания повторяются.
Частоту свободных колебаний называют собственной частотой колебательной системы.
Часто для краткости циклическую частоту называют просто частотой.
Зависимость частоты и периода свободных колебаний от свойств системы.
1. для пружинного маятника
Собственная частота колебаний пружинного маятника равна:
Она тем больше, чем больше жесткость пружины k, и тем меньше, чем больше масса тела m.
Жесткая пружина сообщает телу большее ускорение, быстрее меняет скорость тела, а чем тело массивнее, тем медленнее оно изменяет скорость под влиянием силы.
Период колебаний равен:
Период колебаний пружинного маятника не зависит от амплитуды колебаний.
2. для нитяного маятника
Собственная частота колебаний математического маятника при малых углах отклонения нити от вертикали зависит от длины маятника и ускорения свободного падения:
Период же этих колебаний равен:
Период колебаний нитяного маятника при малых углах отклонения не зависит от амплитуды колебаний.
Период колебаний возрастает с увеличением длины маятника. От массы маятника он не зависит.
Чем меньше g, тем больше период колебаний маятника и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут за сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета (высота 200 м). И это только за счет уменьшения ускорения свободного падения с высотой.