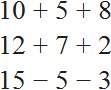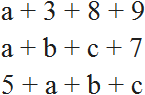Что называется выражением в математике
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
Значение переменной a подставляется в исходное выражение.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
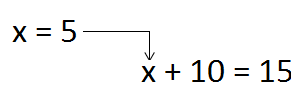
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b
Решение:
Значение выражения
Фраза « выполнить действие » означает выполнить одну из операций действия.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8
Выражение (математика)
В математике, (математическое) выражение — конечная комбинация символов, которая правильно построена согласно правилам, зависящим от контекста.
Математические символы могут обозначать числа (константы), переменные, операции, функции, пунктуацию, группирование и другие аспекты логического синтаксиса.
Содержание
[править] Примеры
Синтаксис выражений варьируется от простого:
до сложного составного:
[править] Формы
Математические выражения включают арифметические, полиномиальные, алгебраические выражения, замкнутые формы, аналитические выражения. Таблица ниже показывает некоторые сходства и различия между ними.
| Арифметические выражения | Полиномиальные выражения | Алгебраические выражения | Замкнутые формы | Аналитические выражения | |
|---|---|---|---|---|---|
| Константа | Да | Да | Да | Да | Да |
| Переменная | Да | Да | Да | Да | Да |
| Арифметическая операция | Да | Да | Да | Да | Да |
| Факториал | Да | Да | Да | Да | Да |
| Целая экспонента | Нет | Да | Да | Да | Да |
| Корень N-ой степени | Нет | Нет | Да | Да | Да |
| Рациональная экспонента | Нет | Нет | Да | Да | Да |
| Иррациональная экспонента | Нет | Нет | Нет | Да | Да |
| Логарифм | Нет | Нет | Нет | Да | Да |
| Тригонометрич. функция | Нет | Нет | Нет | Да | Да |
| Обратная тригонометрич. функция | Нет | Нет | Нет | Да | Да |
| Гиперболическая функция | Нет | Нет | Нет | Да | Да |
| Обратная гиперболическая функция | Нет | Нет | Нет | Да | Да |
| Гамма функция | Нет | Нет | Нет | Нет | Да |
| Функция Бесселя | Нет | Нет | Нет | Нет | Да |
| Специальная функция | Нет | Нет | Нет | Нет | Да |
| Непрерывная функция | Нет | Нет | Нет | Нет | Да |
| Бесконечная последовательность | Нет | Нет | Нет | Нет | Да |
| Формальная степенная последовательность | Нет | Нет | Нет | Нет | Нет |
| Дифференциал | Нет | Нет | Нет | Нет | Нет |
| Предел | Нет | Нет | Нет | Нет | Нет |
| Интеграл | Нет | Нет | Нет | Нет | Нет |
[править] Синтаксис и семантика
[править] Синтаксис
Быть выражением является синтаксическим понятием.
Выражение должно быть правильно построенным: операторы должны иметь нужное количество входов в подходящих позициях, символы, подаваемые на эти входы, должны быть значимыми, и т. д. Цепочки символов, нарушающие правила синтаксиса, построены некорректно и не образуют приемлемого математического выражения.
Например, в обычной арифметической нотации выражение 2 + 3 построено правильно, но следующее выражение непригодно:
[править] Семантика
Семантика изучает значения. Формальная семантика занимается приложением значений к выражениям.
В алгебре выражение может использоваться для обозначения величины,, которая зависит от величин переменных, входящих в выражении. Определение этой величины зависит от семантики, присвоенной символам выражения. Эти семантические правила могут объявить, что некоторые выражения не определяют никакой величины (например, когда они включают деление на 0). Говорят, что такие выражения имеют неопределенное значение, но тем не менее. они — правильно построенные выражения. Вообще говоря, значение выражений не сводится только к обозначению величин; например, выражение может обозначать условие, или уравнение, которое должно быть решено, или может трактоваться как некоторый объект в своем собственном контексте, который управляется согласно определенным правилам. Определенные выражения, которые обозначают величину, одновременно фиксируют необходимое условие, которое считается принятым.
[править] Формальные языки и лямбда-исчисление
Формальные языки позволяют уточнить (формализовать) понятие правильно построенных выражений.
В 1930-х годах новый вид выражений, названных лямбда-выражениями, был введен А. Черчом и С. Клини для определения функций и их вычислений. Эти выражения формируют основание формальной системы лямбда-исчисление, используемой в математической логике и теории языков программирования.
Эквивалентность двух лямбда-выражений неразрешима. Неразрешимость также имеет место для выражений, представляющих действительные числа, построенные из целых чисел с использованием арифметических операций, логарифмов и экспоненциалов (теорема Ричардсона).
[править] Переменные
Многие математические выражения содержат переменные. Некоторая переменная может рассматриваться как свободная или связанная. Для данной комбинации величин свободных переменных выражение может быть вычислено, однако для некоторых других комбинаций значение выражения может остаться неопределенным. Например, выражение
вычисляемое для x = 10, y = 5, дает 2; но оно не определено для y = 0.
Таким образом выражение представляет функцию, входы (аргументы) которой составляют величины, присвоенные свободным переменным, и чей результат — вычисленная величина выражения. Результат вычисление выражения зависит от определения математических операторов и от системы величин, которая является её контекстом.
Говорят, что два выражения эквивалентны, если для каждой комбинации величин свободных переменных, оба выражения дают тот же самый результат, то есть они представляют одну и ту же функцию. Например, выражение
имеет свободную переменную x, связанную переменную n, константы 1, 2, и 3, два вхождения неявного (имплицитного) оператора умножения, и оператор суммирования. Выражение эквивалентно более простому выражению 12x. Значение для x = 3 и n=3 равно 36.
Числовые и алгебраические выражения. Преобразование выражений.
Что такое выражение в математике? Зачем нужны преобразования выражений?
Допустим, перед вами злой пример. Очень большой и очень сложный. Допустим, вы сильны в математике и ничего не боитесь! Сможете сразу дать ответ?
Вам придётся решать этот пример. Последовательно, шаг за шагом, этот пример упрощать. По определённым правилам, естественно. Т.е. делать преобразование выражений. Насколько успешно вы проведёте эти преобразования, настолько вы и сильны в математике. Если вы не умеете делать правильные преобразования, в математике вы не сможете сделать ни-че-го.
Во избежание такого неуютного будущего (или настоящего. ), не мешает разобраться в этой теме.)
Для начала выясним, что такое выражение в математике. Что такое числовое выражение и что такое алгебраическое выражение.
Что такое выражение в математике?
В общем виде термин «математическое выражение» применяется, чаще всего, чтобы не мычать. Спросят вас, что такое обыкновенная дробь, например? И как ответить?!
Первый вариант ответа: «Это. м-м-м-м. такая штука. в которой. А можно я лучше напишу дробь? Вам какую?»
Второй вариант как-то посолидней будет, правда?)
Вот в этих целях фраза «математическое выражение» очень хороша. И правильно, и солидно. Но для практического применения надо хорошо разбираться в конкретных видах выражений в математике.
Числовые выражения.
Что такое числовое выражение? Это очень простое понятие. Само название намекает, что это выражение с числами. Да, так оно и есть. Математическое выражение, составленное из чисел, скобок и знаков арифметических действий называется числовым выражением.
тоже числовое выражение, да.
Когда числовое выражение не имеет смысла?
Понятное дело, если мы видим перед собой какую-то абракадабру, типа
то делать ничего и не будем. Так как непонятно, что с этим делать. Бессмыслица какая-то. Разве что, посчитать количество плюсиков.
Но бывают внешне вполне благопристойные выражения. Например такое:
Чтобы дать такой ответ, пришлось, конечно, посчитать, что в скобочках будет. А иногда в скобочках такого понаворочено. Ну тут уж ничего не поделаешь.
Алгебраические выражения.
и так далее, до бесконечности. )
В арифметике можно записать, что
А вот если мы подобное равенство запишем через алгебраические выражения:
мы сразу решим все вопросы. Для всех чисел махом. Для всего бесконечного количества. Потому, что под буквами а и b подразумеваются все числа. И не только числа, но даже и другие математические выражения. Вот так работает алгебра.
Когда алгебраическое выражение не имеет смысла?
Про числовое выражение всё понятно. Там на ноль делить нельзя. А с буквами, разве можно узнать, на что делим?!
Возьмём для примера вот такое выражение с переменными:
Конечно. Просто в таких случаях говорят, что выражение
имеет смысл для любых значений а, кроме а = 5.
Весь набор чисел, которые можно подставлять в заданное выражение, называется областью допустимых значений этого выражения.
Как видите, ничего хитрого нет. Смотрим на выражение с переменными, да соображаем: при каком значении переменной получается запретная операция (деление на ноль)?
А потом обязательно смотрим на вопрос задания. Чего спрашивают-то?
Если спрашивают, при каком значении переменной выражение не имеет смысла, наше запретное значение и будет ответом.
Если спрашивают, при каком значении переменной выражение имеет смысл (почувствуйте разницу!), ответом будут все остальные числа, кроме запретного.
Зачем нам смысл выражения? Есть он, нет его. Какая разница?! Дело в том, что это понятие становится очень важным в старших классах. Крайне важным! Это основа для таких солидных понятий, как область допустимых значений или область определения функции. Без этого вы вообще не сможете решать серьёзные уравнения или неравенства. Вот так.
Преобразование выражений. Тождественные преобразования.
Мы познакомились с числовыми и алгебраическими выражениями. Поняли, что означает фраза «выражение не имеет смысла». Теперь надо разобраться, что такое преобразование выражений. Ответ прост, до безобразия.) Это любое действие с выражением. И всё. Вы эти преобразования делали с первого класса.
Возьмём крутое числовое выражение 3+5. Как его можно преобразовать? Да очень просто! Посчитать:
Вот этот расчёт и будет преобразованием выражения. Можно записать то же самое выражение по-другому:
Тут мы вообще ничего не считали. Просто записали выражение в другом виде. Это тоже будет преобразованием выражения. Можно записать вот так:
Любое действие над выражением, любая запись его в другом виде называется преобразованием выражения. И все дела. Всё очень просто. Но есть здесь одно очень важное правило. Настолько важное, что его смело можно назвать главным правилом всей математики. Нарушение этого правила неизбежно приводит к ошибкам. Вникаем?)
Предположим, мы преобразовали наше выражение как попало, вот так:
Преобразование? Конечно. Мы же записали выражение в другом виде, что здесь не так?
Всё не так.) Дело в том, что преобразования «как попало» математику не интересуют вообще.) Вся математика построена на преобразованиях, в которых меняется внешний вид, но суть выражения не меняется. Три плюс пять можно записать в каком угодно виде, но это должно быть восемь.
Преобразования, не меняющие сути выражения называются тождественными.
Именно тождественные преобразования и позволяют нам, шаг за шагом, превращать сложный пример в простое выражение, сохраняя суть примера. Если в цепочке преобразований мы ошибёмся, сделаем НЕ тождественное преобразование, дальше мы будем решать уже другой пример. С другими ответами, которые не имеют отношения к правильным.)
Вот оно и главное правило решения любых заданий: соблюдение тождественности преобразований.
Пример с числовыми выражением 3+5 я привёл для наглядности. В алгебраических выражениях тождественные преобразования даются формулами и правилами. Скажем, в алгебре есть формула:
Как вы, наверняка, догадались, эту цепочку можно продолжать до бесконечности. ) Очень важное свойство. Именно оно позволяет превращать всякие монстры-примеры в белые и пушистые.)
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
А вот здесь можно познакомиться с функциями и производными.