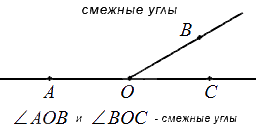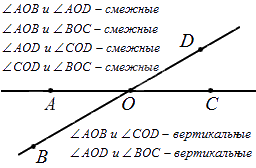Что называется вершиной угла

Что называется вершиной угла

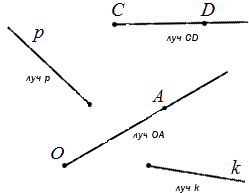
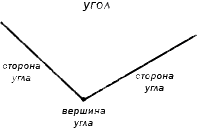
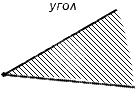
Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, то есть два луча с общим началом называются углом. Лучи, образующие угол, называются сторонами угла, а их общее начало — вершиной угла.

Обозначение углов

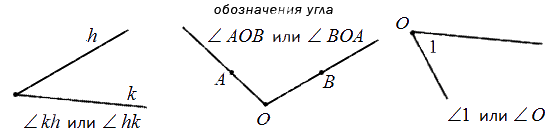
Угол обозначается или одной буквой или цифрой, поставленной при вершине угла, например угол A или угол 1, или тремя буквами, из которых одна стоит при его вершине, а две другие при каких-либо точках его сторон. При обозначении угла тремя буквами, буква, стоящая при его вершине, произносится и пишется между двумя другими, например угол AOB. Слово угол в записи заменяют знаком ∠, например ∠1.

Внутренняя и внешняя область

Два луча, исходящие из одной точки, образуют два угла. Для обозначения нужного угла, угол обычно помечается дугой:

Если рассматриваются оба угла, образованные двумя лучами, то они помечаются разным числом дуг, но только в том случае, если углы не равны. Равные углы обозначаются одинаково.

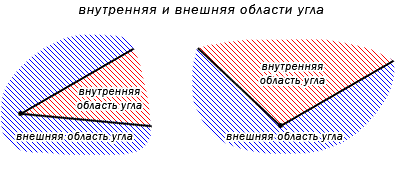
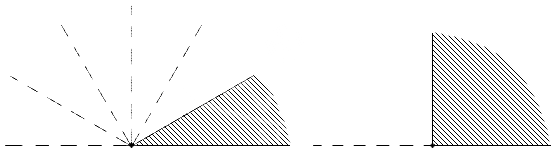
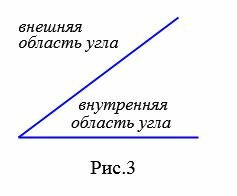
Любой угол делит плоскость на две области. Одна область обычно называется внутренней, а другая внешней. Внутренняя область угла — это часть плоскости, расположенная между сторонами рассматриваемого угла:

Внешняя область угла — это часть плоскости, которая не принадлежит рассматриваемому углу.

Источник

Что называется вершиной угла

Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.

Лучи называются сторонами угла, а их общее начало − вершиной угла.

Обозначение угла

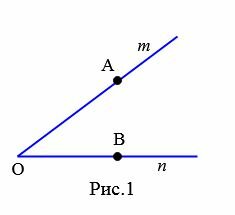
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)

Развернутый угол. Внутренняя и внешняя область угла

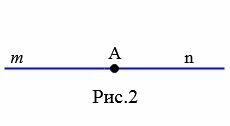
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.

Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).

Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.

Фигуру, состоящую из угла и его внутренней области также называют углом.

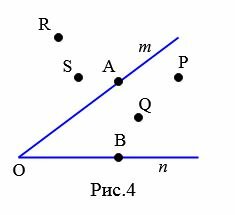
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.

Типы углов

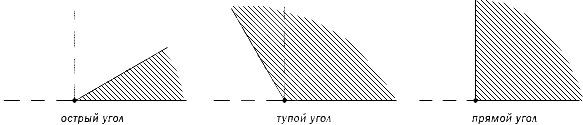
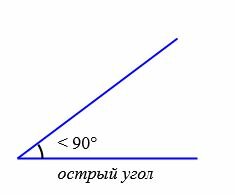
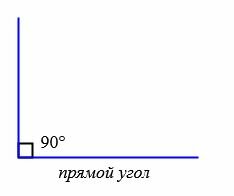
В зависимости от величин, углы бывают следующих типов (Рис.5):

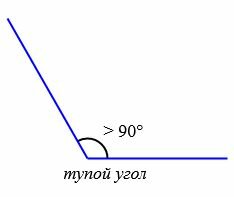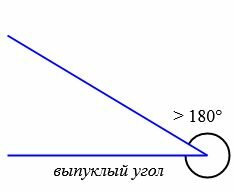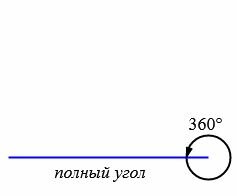Сравнение углов

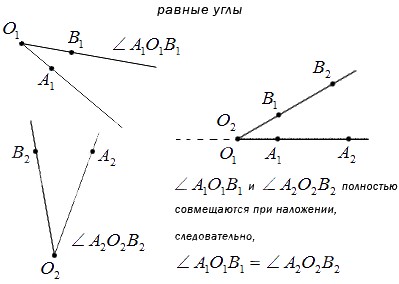
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.

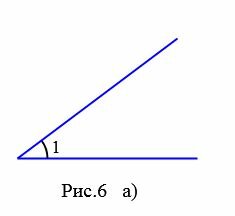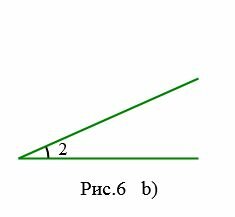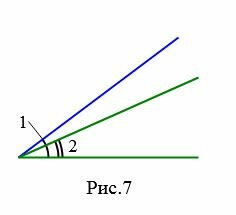
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)

Градусная мера угла

Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).

Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)

Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.

Источник

Угол. Основные понятия.

Когда два луча (AO и OB) исходят из одной точки, то фигура, сформированная этими лучами (вместе с частью плоскости, ограниченной ими), называется углом.

Стороны угла следует представлять себе бесконечно продолженными от вершины.

Угол обыкновенно обозначается тремя буквами, из которых средняя ставится у вершины, а крайние у каких-нибудь точек сторон. Например, говорят “угол АОВ или угол ВОА”. Но можно обозначать угол и одной буквой, поставленной у вершины, если при этой вершине других углов нет. Мы иногда будем обозначать угол цифрой, поставленной внутри угла у вершины. Слово “угол” на письме часто заменяется знаком /.

Когда два луча исходят из одной точки, то строго говорят, что они образуют не один угол, а два угла.

Эти два угла равны друг другу лишь в том случае, когда лучи AO и OB составляют одну прямую.

Такой угол называют развернутым углом.

Два угла считаются равными углами, если при наложении они могут совместиться.

Мы принимаем как очевидное, что внутри всякого угла из его вершины можно провести луч (и притом только один), который делит этот угол пополам. Такой луч называется биссектрисой угла.

Два угла (AOB и BOС) называются смежными, если одна сторона у них общая, а две другие стороны составляют прямую линию.

Когда два смежных угла равны (черт. 2), то общая сторона их OB называется перпендикуляром к прямой AC, на которой лежат другие стороны.

Если же смежные углы неравны (черт. 1), то общая сторона OB называется наклонной к AC.

В том и в другом случае точка O называется основанием (перпендикуляра или наклонной).

Из всякой точки прямой можно, по ту и другую сторону от этой прямой, восставить к ней перпендикуляр и притом только один.

Всякий развернутый углом равен 2 d = 180°.

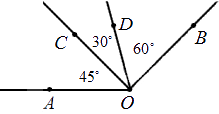
Всякий угол (АОС), меньший прямого угла (АОВ) называется острым.

Всякий угол (AOD) больший прямого называется тупым.

Источник

Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение угла

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Внутренняя область угла – элемент, служащий для второго определения угла.

Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.

Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.

Определение смежных и вертикальных углов

Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.

На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.

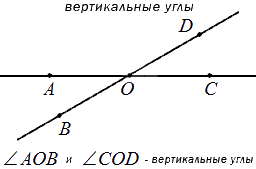
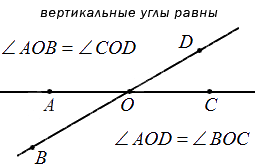
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.

При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.

Сравнение углов

Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.

Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.

Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.

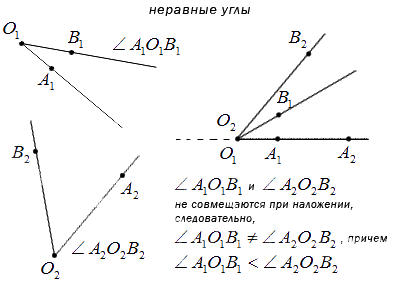
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.

Развернутые углы являются равными.

Измерение углов

Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.

Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.

Чаще всего используют понятие градус.

Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.

Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.

Минутой называют одну шестидесятую часть градуса.

Секундой называют одну шестидесятую часть минуты.

Градус содержит 3600 секунд. Минуты обозначают « ‘ », а секунды « » ». Имеет место обозначение:

Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.

Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.

Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.

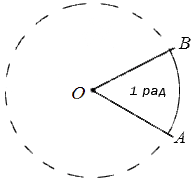
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.

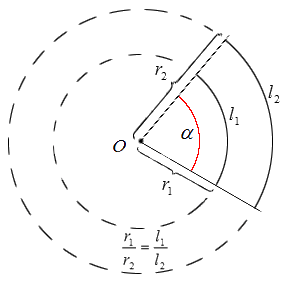
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.

Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.

На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.

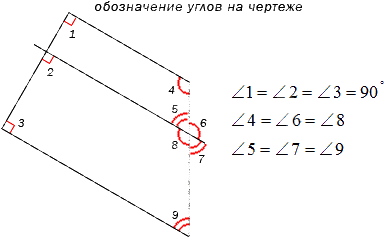
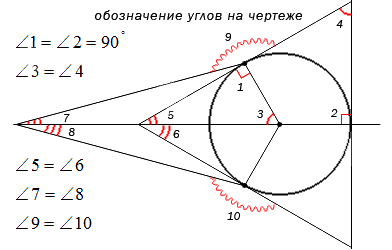
Обозначение углов на чертеже

Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.

Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.

Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.

Источник

Что такое многоугольник в математике — виды, свойства и примеры фигур с названиями

Геометрическую фигуру, ограниченную со всех сторон ломанной линией, называют многоугольником. В математике такое понятие применимо для множества объектов, образованных из трёх и более отрезков. Фигуры, относящиеся к этому классу, могут иметь как произвольную форму, так и строгую. Например, семиугольник, квадрат. Но при этом их всех объединяют одинаковые свойства и ряд правил.

Общие сведения

Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.

Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.

Любого вида многоугольник состоит из следующих частей:

Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.

Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.

Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.

А также все многоугольники разделяют на 2 типа — выпуклые и невыпуклые. Тело хотя бы с одним углом, смотрящим внутрь, относится ко второму типу, а тот, чьи углы направлены наружу — к первому. В школьном курсе геометрии изучают только второй вид, расположенный на плоскости. Более сложными видами многоугольников занимается стереометрия и планиметрия.

Простейшие четырёхугольники

Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.

Наиболее часто приходится сталкиваться со следующими видами:

Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.

Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.

Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.

Треугольный многоугольник

Такую фигуру называют треугольником. Она состоит из трёх углов и такого же числа сторон. Их, принято обозначать маленькими буквами a, b, c или подписывать двумя заглавными по названиям вершин, которые являются началом и концом отрезка. Например, треугольник ABC содержит стороны: AB = a, BC = b, AC = c.

В зависимости от особенностей, фигура может называться:

Но несмотря на классификацию, все перечисленные виды обладают общими свойствами. Считается, что угол любого плоского треугольника образуется при пересечении двух лучей, содержащих его стороны, то есть если говорят об ∠A, то подразумевают, что был лучи AB и АС, при построении которых он и образовался. Таким образом, он заключается не между сторонами, а лучами.

Как и для любого другого многоугольника, у треугольника есть периметр и площадь. Следуя из определения первого, для фигуры с вершинами ABC он будет равен сумме длин всех сторон: P = a + b + c. У треугольников существуют так называемые замечательные линии: медиана, биссектриса, высота.

Эти 3 параметра определяют свойства треугольной фигуры. С их помощью можно находить, площадь, стороны, значения углов. Определение медианы звучит так: это прямая, проведённая из угла к противолежащей стороне таким образом, что разделяет её пополам. Под биссектрисой же понимают отрезок, разделяющий угол на 2 равные части. Высотой называют перпендикуляр, опущенный на противоположную сторону из вершины.

Треугольник, который выглядит, как прямой угол, называют прямоугольным. То есть построив в любом многоугольнике с тремя углами высоту, можно получить две фигуры, обе из которых точно будут прямоугольными. Боковые грани, перпендикулярные друг другу, называют катетами, а оставшуюся сторону — гипотенузой. По сути, тело представляет собой разделённый диагональю квадрат. Отсюда площадь многоугольника будет равняться произведению катетов, делённых на 2: S = a*b/2. А также следует отметить, что у равнобедренного треугольника медиана, высота и биссектриса совпадают.

Теорема об углах

Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.

Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.

Источник