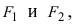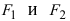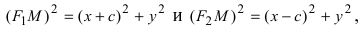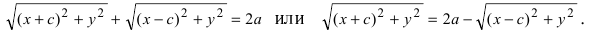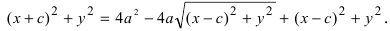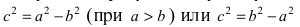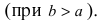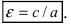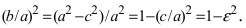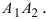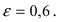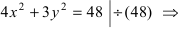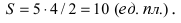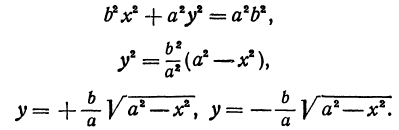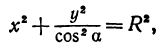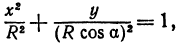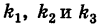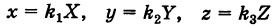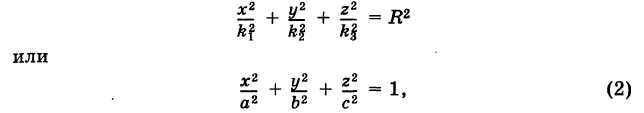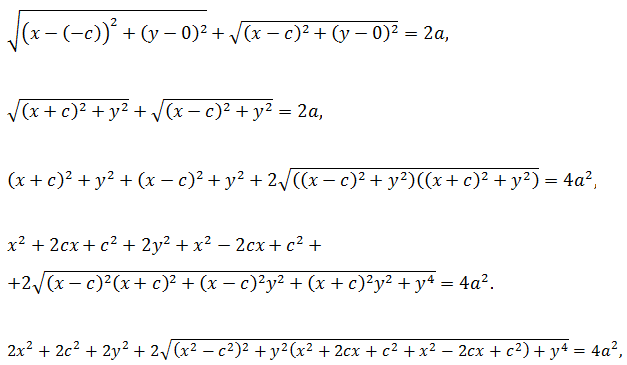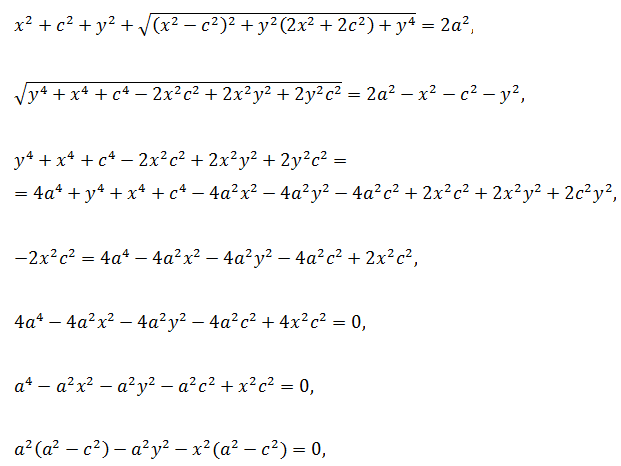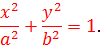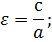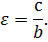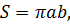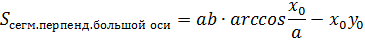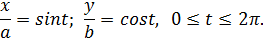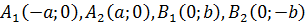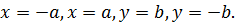Что называется вершинами эллипса
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 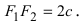
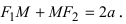
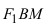
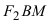
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Определение: Найденные точки называются вершинами эллипса.
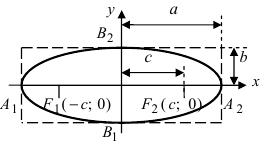
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 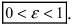
Если 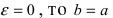
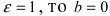
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 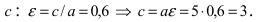
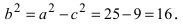
Пример:
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
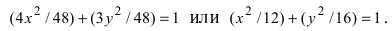
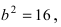
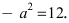
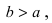
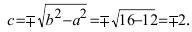
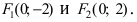
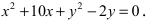
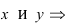
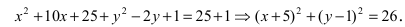
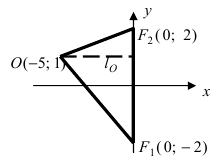
Построим в декартовой системе координат треугольник 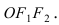
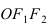
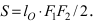
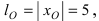
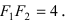
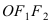
Эллипс в высшей математике
где 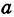
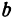
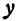
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
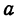

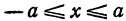
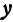
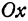
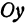
При 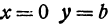
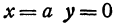
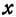

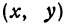
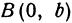
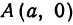
Полученная линия называется эллипсом. Число 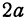
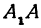
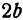
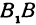
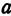
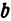
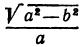
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
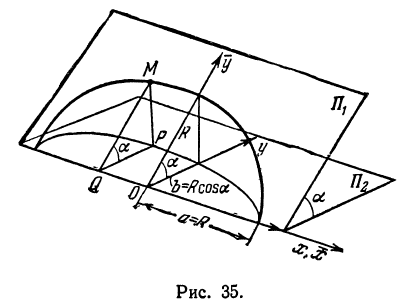
Возьмем две плоскости, пересекающиеся под углом 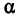
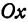
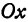
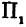
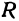
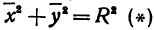
Пусть точка 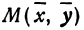
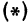
Обозначим проекцию точки 
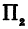
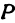
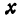
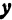


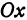
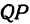
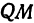
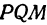
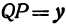
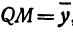
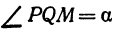
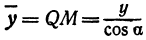


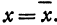
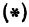
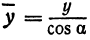
а это есть уравнение эллипса с полуосями 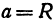
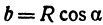
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 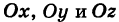
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 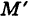
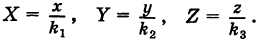
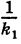
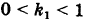
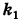
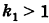
Подставляя эти формулы в уравнение (1), будем иметь
где 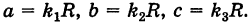
Величины 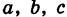
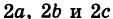
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Эллипс
Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
\frac
$$
при условии \(a \geq b > 0\).
Из уравнения \eqref
Рис. 8.1. Эллипс
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса \(a\) с центром в центре эллипса: \(x^<2>+y^<2>=a^<2>\). При каждом \(x\) таком, что \(|x| Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении \(b/a\).
Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Фокусами называются точки \(F_<1>\) и \(F_<2>\) с координатами \((c, 0)\) и \((-c, 0)\) в канонической системе координат (рис. 8.3).
Рис. 8.3. Фокусы эллипса.
Для окружности \(c=0\), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Отметим, что \(\varepsilon Утверждение 2.
Расстояние от произвольной точки \(M(x, y)\), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы \(x\):
$$
r_<1>=|F_<1>M|=a-\varepsilon x,\ r_<2>=|F_<2>M|=a+\varepsilon x.\label
$$
Очевидно, что \(r_<1>^<2>=(x-c)^<2>+y^<2>\). Подставим сюда выражение для \(y^<2>\), найденное из уравнения эллипса. Мы получим
$$
r_<1>^<2>=x^<2>-2cx+c^<2>+b^<2>-\frac
$$
Учитывая равенство \eqref
$$
r_<1>^<2>=a^<2>-2cx+\frac
$$
Так как \(x \leq a\) и \(\varepsilon Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса \(2a\).
Необходимость. Если мы сложим равенства \eqref
$$
r_<1>+r_<2>=2a.\label
$$
Достаточность. Пусть для точки \(M(x, y)\) выполнено условие \eqref
$$
\sqrt<(x-c)^<2>+y^<2>>=2a-\sqrt<(x+c)^<2>+y^<2>>.\nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^<2>=a\sqrt<(x+c)^<2>+y^<2>>.\label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение \eqref
Рис. 8.4. Фокусы и директрисы эллипса.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса \(\varepsilon\).
Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть \(M_<0>(x_<0>, y_<0>)\) — точка на эллипсе и \(y_ <0>\neq 0\). Через \(M_<0>\) проходит график некоторой функции \(y=f(x)\), который целиком лежит на эллипсе. (Для \(y_ <0>> 0\) это график \(f_<1>(x)=b\sqrt<1-x^<2>/a^<2>>\), для \(y_ <0>Утверждение 5.
Касательная к эллипсу в точке \(M_<0>(x_<0>, y_<0>)\) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Рис. 8.5.
Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.
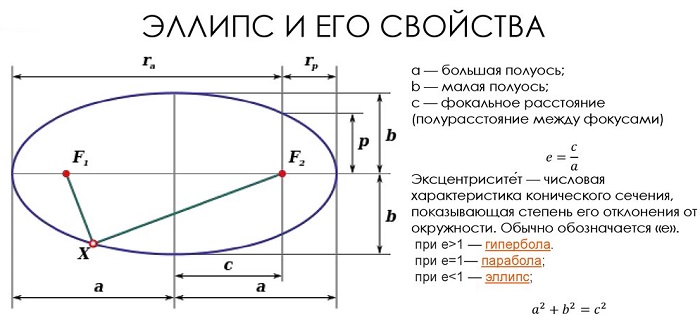
Определение и элементы эллипса
Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.
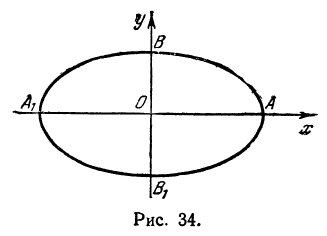
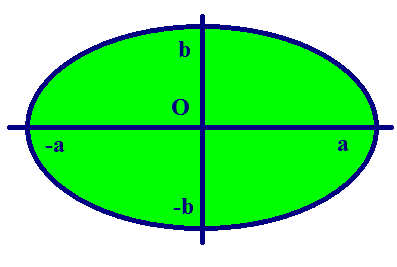
По форме график эллипса представляет замкнутую овальную кривую:
Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.
Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.
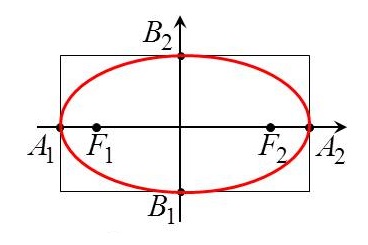
Точки эллипса, являющиеся концами осей, называются вершинами.
Расстояния от точки на линии до фокусов получили название фокальных радиусов.
Расстояние между фокусами есть фокальное расстояние.
Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.
Основные свойства эллипса
имеются две оси и один центр симметрии;
при равенстве полуосей линия превращается в окружность;
все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.
Уравнение эллипса
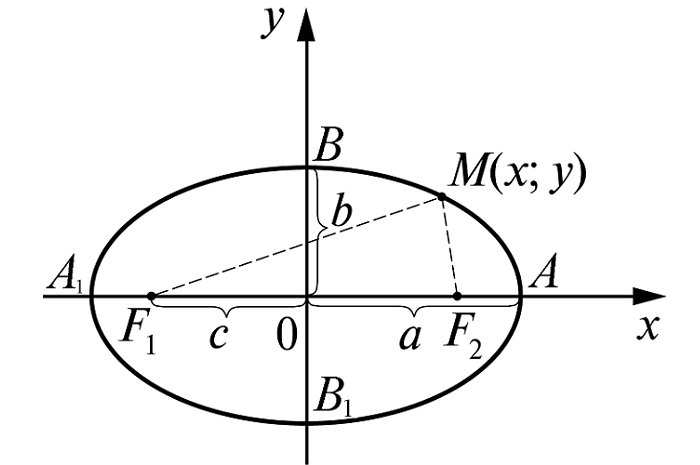
Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.
Для составления уравнения достаточно воспользоваться определением, введя обозначение:
а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);
c – половина фокального расстояния;
M(x;y) – произвольная точка линии.
В этом случае фокусы находятся в точках F1(-c;0); F2(c;0)
После ввода ещё одного обозначения
получается наиболее простой вид уравнения:
Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).
В случае (b b) формула эксцентриситета (ε) принимает вид:
Чем меньше эксцентриситет, тем более сжатым будет эллипс.
Площадь эллипса
Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:
a – большая полуось, b – малая.
Площадь сегмента эллипса
Часть эллипса, отсекаемая прямой, называется его сегментом.
Длина дуги эллипса
Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:
Радиус круга, вписанного в эллипс
В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:
Радиус круга, описанного вокруг эллипса
Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:
Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.
Как построить эллипс
Построение линии удобно выполнять в декартовых координатах в каноническом виде.
Строится прямоугольник. Для этого проводятся прямые:
Сглаживая углы, проводится линия по сторонам прямоугольника.
Полученная фигура есть эллипс. По координатам отмечается каждый фокус.
При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.