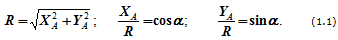Что называется условными связями
Техническая механика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
2. Связи и реакции связей
Все тела делятся на свободные и связанные.
Свободные тела — это тела, перемещение которых не ограничено.
Связанные тела — это тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Связи делятся на несколько типов.
Связь — гладкая опора (без трения) — реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
Гибкая связь (нить, веревка, трос, цепь) — груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень — стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.
Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир. Точка крепления перемещаться не может.
Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (Rx, Ry).
Защемление, или «заделка». Любые перемещения точки крепления невозможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Мz, препятствующий повороту.
Реактивная сила представляется в виде двух составляющих вдоль осей координат:
ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
СВЯЗИ И ИХ КЛАССИФИКАЦИЯ
Связями называют любого вида ограничения, налагаемые на положения (координаты) и скорости точек механической системы.
,
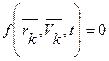
Примером удерживающей связи может служить система из двух материальных точек т1 и т2, которые соединены стержнем постоянной длины L. В этом случае уравнение связи имеет вид
.
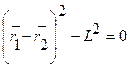
Неудерживающими связями называются связи, которые могут в некоторые промежутки времени меняться. Аналитически они выражаются неравенством, связывающим координаты точек системы, их скорости и время
.
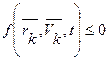
Примером неудерживающей связи может служить система из двух материальных точек, которые соединены гибкой нитью длинной L. В этом случае уравнение связи имеет вид
/
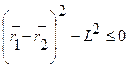
В дальнейшем будем рассматривать только удерживающие связи.
Связь называется стационарной, если она не меняется с течением времени. В уравнение стационарной связи не входит время t в явном виде.
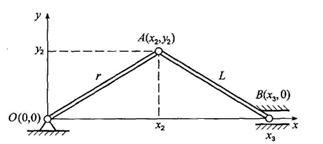
Примером механизма, имеющего стационарные связи, может служить кривошипно-шатунный механизм. Механизм состоит из кривошипа ОА длинной r, шатуна АВ длинной L и ползуна В.
Уравнения связи данного механизма запишутся:
,
.
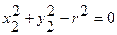
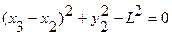
Связь называется нестационарной, если она меняется с течением времени. Уравнение такой связи содержит время t явно.
Например, материальная точка может двигаться только по поверхности. Пусть уравнение поверхности задано в виде функции f(х,у,z) = 0. Это стационарная связь. Если поверхность подвижная или деформирующаяся, то в уравнение поверхности время г войдет явно: f(х,у,z,t) = 0. В этом случае связь нестационарная. Примером нестационарной связи является, также деформируемое твердое тело.
Связь называется конечнойили геометрической, если она накладывает ограничения только на координаты точек системы. Уравнение конечной (геометрической) связи имеет вид
.
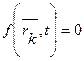
Эта связь не налагает ограничение на скорости точек системы.
В общем случае удерживающая связь называется кинематическойили дифференциальной. Эта связь налагает ограничения на положение координат точек системы и на скорости этих точек.
Если кинематическая (дифференциальная) связь интегрируется, то после интегрирования связь перестает быть таковой и становиться конечной (геометрической) связью. Следовательно, связь будет кинематической (дифференциальной) только в том случае, если она неинтегрируемая.
Система называется склерономной, если на нее наложены только стационарные связи. В противном случае система называется реономной.
Голономной называется всякая свободная система материальных точек, а также несвободная система с конечными или дифференциальными, но интегрируемыми связями. При наличии дифференциальных неинтегрируемых связей, система называется неголономной.
Рассмотрим пример голономной связи. Колесо радиуса R катиться без скольжения по прямолинейному рельсу.
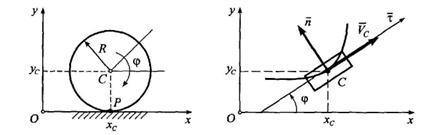
Положение колеса в плоскости движения хОу определяется координатами центра колеса (полюса) хс, ус и углом поворота φ. Если
Кроме того, должна быть равна нулю скорость точки Р, точки касания колеса с рельсом. Это условие запишется в виде уравнения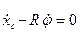 
.. Последнее уравнение накладывает ограничения на скорости, поэтому связь будет дифференциальной (кинематической). Но это уравнение сразу интегрируется и приводит к соотношению между координатами хс и φ, имеющему вид хс=Rφ. Таким образом, рассмотренная система является голономной.
Силы, приложенные к точкам системы, обычно классифицируют двумя способами.
По первому способу, совокупность всех сил, приложенных к точкам материальной системы, разделяют на внутренние и внешние силы. Внутренними силами (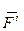
) называют силы взаимодействия между точками, образующими материальную систему. Внешними силами (
) называют силы, возникающие благодаря воздействию на точки системы других материальных точек, не входящих в эту систему.
В соответствии со вторым способом классификации, совокупность всех сил, приложенных к точкам материальной системы, разделяют на активные и пассивные силы. Силы, которые создают или способны создавать движение твердого тела, называются активными силами. Силы, не создающие движение, но ограничивающие перемещения твердого тела (например, реакции опор) относятся к пассивным силам.
Отметим, что деление системы сил на внутренние и внешние силы и на активные и пассивные силы не взаимосвязаны.
Для задач, связанных с механикой деформируемого твердого тела используют первую классификацию: делят совокупность приложенных к точкам материальной системы сил на внутренние и внешние.
В аналитической механике эффект действия силы на тело определяется бесконечно малыми перемещениями тела, допускаемые наложенными связями.
Так, для груза, расположенного на наклонной плоскости, таким перемещением (допускаемым связью) будет перемещение 
— движение груза вдоль наклонной плоскости.
В аналитической механике эффект действия связи определяется возможными перемещениями точек.
условная связь
Смотреть что такое «условная связь» в других словарях:
Условная энтропия — Энтропия (информационная) мера хаотичности информации, неопределённость появления какого либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения. Например, в… … Википедия
Звуковой символизм — условная связь между звуковым оформлением слова и его эмоциональной окраской. З. с. используется в поэтической речи. Например, звук «л» кажется «подходящим» для обозначения чего то мягкого, ласкового, поэтического (ср. у К. Бальмонта… … Большая советская энциклопедия
УСЛОВНЫЕ РЕФЛЕКСЫ — УСЛОВНЫЕ РЕФЛЕКСЫ. Условный рефлекс теперь отдельный физиол. термин, обозначающий определенное нервное явление, подробное изучение которого повело к образованию нового отдела в физиологии животных ф и з и о логии высшей нервной деятельности как… … Большая медицинская энциклопедия
Русское личное имя — Святцы (Печатный двор, 1646 год) … Википедия
АССОЦИАЦИЯ — (от позднелат. associatio соединение) в психологии, связь, образующаяся при определ. условиях между двумя или более психич. образованиями (ощущениями, двигат. актами, восприятиями, представлениями, идеями и т. п.); действие этой связи… … Философская энциклопедия
МЕГАРСКАЯ ШКОЛА, мегарики — МЕГАРСКАЯ ШКОЛА, мегарики (οἱ Μεγαρικοί) (4 нач. 3 в. до н. э.), одна из сократических школ; основана Евклидом из Мегары. Принято выделять три этапа существования Мегарской школы, на основании свидетельства Диогена Лаэртия о том, что… … Античная философия
закон клавия — логический закон, характеризующий связь импликации ( если, то ) и отрицания. Его можно передать так: если из отрицания некоторого высказывания вытекает само это высказывание, то оно является истинным. Или короче: высказывание, вытекающее из… … Словарь терминов логики
транзитивности закон — закон логики, согласно которому определенная логическая связь (импликация, эквивалентность и др.) представляет собой отношение транзитивности. Т. з. для условного высказывания (импликации) можно передать так: когда верно, что если первое, то… … Словарь терминов логики
Парадокс импликации — Парадоксы импликации это парадоксы, возникающие в связи с содержанием условных утверждений классической логики. Главная функция этих утверждений обоснование одних утверждений ссылкой на другие. Содержание 1 Смысл импликации … Википедия
РЕЛЕВАНТНАЯ ЛОГИКА — РЕЛЕВАНТНАЯ ЛОГИКА направление в символической логике (см. Логика символическая), которое возникло и развивалось в качестве альтернативы классической символической логике. В названии “релевантная” (термины “релевантный”, “релевантность”… … Философская энциклопедия
релевантная логика — РЕЛЕВАНТНАЯ ЛОГИКА (от англ. relevant существенный) одно из направлений современной неклассической логики, сформировавшееся во второй половине 20 в. Ее возникновение связано с попыткой решить проблему формализации логического следования и … Энциклопедия эпистемологии и философии науки
iSopromat.ru
Связями в механике называются любого вида ограничения, накладываемые на положения, скорости точек механической системы, независящие от действующих сил.
Связи неизменяемые со временем называются стационарными, изменяемые – нестационарными.
Связи бывают удерживающие, когда ограничения сохраняются при любом положении системы и неудерживающие, которые этим свойством не обладают.
Связи, налагающие ограничения на координаты точек системы называются геометрическими, а накладывающие ограничения на скорости точек системы кинематическими или дифференциальными.
Если дифференциальную связь можно представить как геометрическую (проинтегрировать), то такая связь называется интегрируемой, в противном случае не интегрируемой.
Геометрические интегрируемые дифференциальные связи называются голономными, а неинтегрируемые дифференциальные связи неголономными. Соответственно и системы разделяют на голономные (с голономными связями) и неголономные (с неголономными связями).
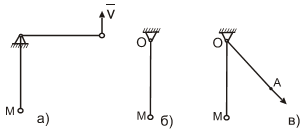
Пример. На рис. 1.1а, шарик М в плоскости закреплен через стержень с шарниром О – стационарная удерживающая голономная связь
V=ω ∙ l, интегрируем S=φ ∙ l.
Рис. 1.1в, – нить продернута в кольцо О, конец А нити движется со скоростью u — неудерживающая нестационарная связь, ее уравнение:
x 2 + y 2 — (l0+ u ∙ t) 2 ≤ 0
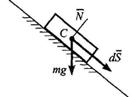
Эффект механических связей можно учитывать и рассматривая перемещения, которые допускаются наложенными связями. Возможными перемещениями механической системы называется любая совокупность элементарных (бесконечно малых) перемещений точек системы из занимаемого в данный момент времени положения, которое допускается наложенными на систему связями. Связи называются идеальными, если сумма элементарных работ их реакций на любом возможном перемещении равна нулю.
Например: тело на гладкой поверхности, реакция опоры направлена по нормали к поверхности, δS — возможное перемещение (рис. 1.2).
iSopromat.ru
Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.
Реакции связей — это усилия, с которыми связи действуют на данное тело.
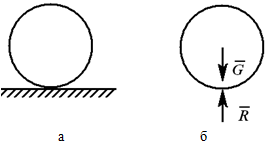
Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Подробнее про связи и реакции связей смотрите в нашем видео:
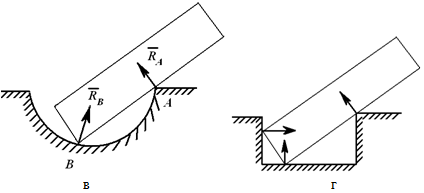
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными. Ниже приведены примеры замены связей их реакциями. На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.
Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1). Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль троса (нити, цепи, стержня) (рисунок 1.2).
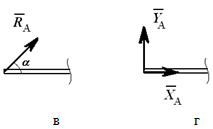
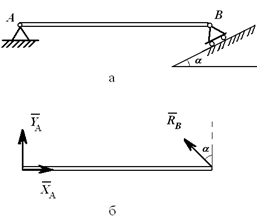
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3, а или 1.3, б). Она может быть заменена либо силой R с углом α (рисунок 1.3, в), либо двумя силами, например, XA и YA (рисунок 1.3, г).
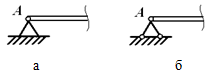
Всегда можно перейти от R и α к XA и YA (и наоборот):
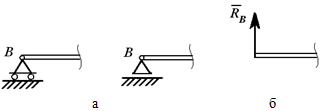
Шарнирно-подвижная опора (рисунок 1.4, а) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности (рисунок 1.4, б).
Связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), их действие заменено силами XA, YA и RB.
Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросим втулку – получим действие на стержень силы RD и момента MD.
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет момент MC (рисунок 1.7, б).
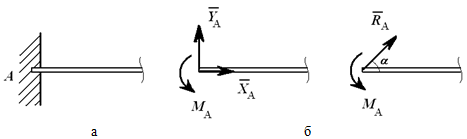
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA) и момент ΜA (рисунок 1.8).
На рисунках 1.9 – 1.15 показаны примеры замены сил, расположенных в пространстве, их реакциями.
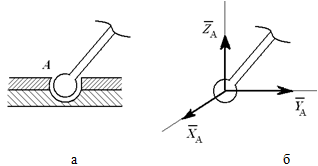
Шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменена системой сил (рисунок 1.9, б) XA, YA и ZA, т.е. силой, неизвестной по величине и направлению.
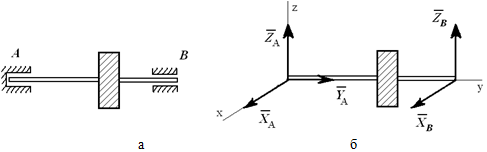
На рисунке 1.10, а показан вал, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами XA, YA, ZA и XB, ZB (рисунок 1.10, б).
На рисунках 1.11 и 1.12 приведены примеры замены различных связей их реакциями.