Что называется ускорением равноускоренного движения

Что называется ускорением равноускоренного движения? Формулы и решение задачи

Понятие об ускорении

Движение объектов вдоль различных траекторий описывается такими величинами, как путь, скорость и ускорение. Понятия пути и скорости интуитивно понятны каждому человеку. Математическая формула, связывающая путь L и скорость v¯, имеет вид

Отметим один важный момент в этом определении: в нем речь идет о любом изменении скорости, которое может проявляться как в изменении ее модуля, так и направления.

Подставляя явное выражение для скорости в последнюю формулу, можно получить еще одно математическое равенство для ускорения через вторую производную пути:

Ускорение в системе СИ измеряют в метрах в квадратную секунду (сокращенно записывается м/с2). Так, величина 1 м/с2 означает, что скорость движения тела за каждую секунду возрастает на 1 м/с.

Равноускоренное движение и ускорение

Что называется ускорением движения равноускоренного? Понять это можно, если рассмотреть указанный тип движения.

Если движение является криволинейным, то направление ускорения изменяется, однако формула выше остается все равно справедливой, поскольку она описывает так называемую тангенциальную компоненту ускорения.

Прямолинейное движение с ускорением

Это движение происходит по прямой линии. В общем случае путь, пройденный за время t телом, рассчитывается по формуле

Приведенное кинематическое уравнение движения позволяет вычислить ускорение, если известен момент времени t и путь L, который тело прошло до этого момента. Искомое выражение имеет форму

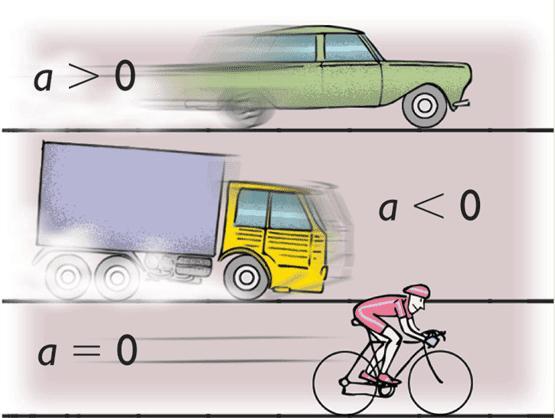
Примером равноускоренного движения является разгон автомобиля или велосипедиста после старта. Вектор ускорения в рассмотренном случае совпадает с вектором скорости.

Движение по окружности с ускорением

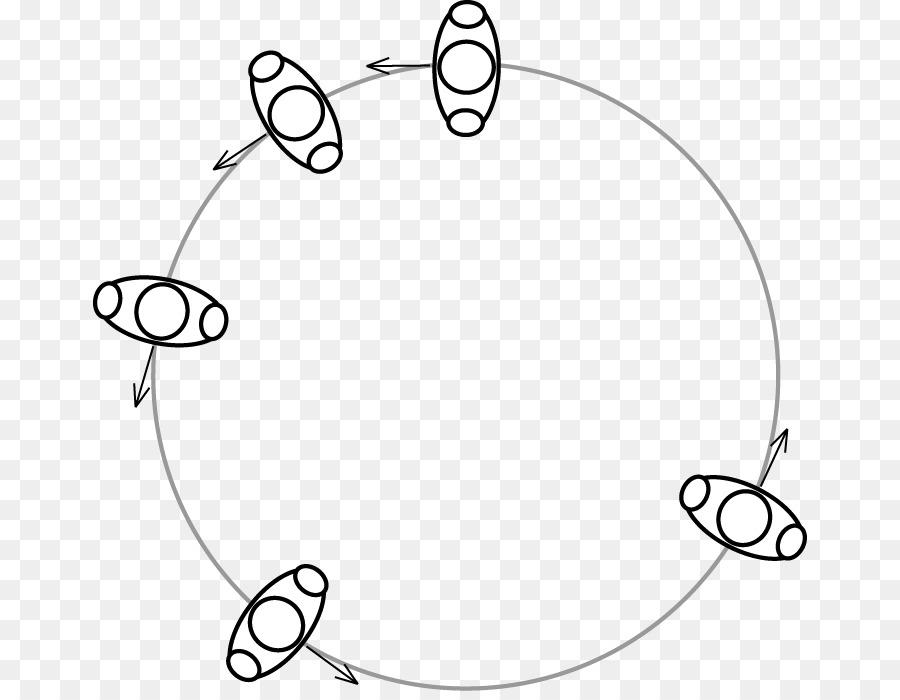
Помимо прямолинейного движения в технике и природе встречается часто перемещение объектов по окружности. Оно может быть как равномерным, например вращение планет по своим орбитам, так и ускоренным, например вращение валов и шестерен механических станков.

Что называется ускорением равноускоренного движения тела по окружности? Его принято рассчитывать по следующей формуле:

Кинематическое уравнение движения для равноускоренного вращения имеет вид

Формула, которая связывает линейное (тангенциальное) ускорение с угловым, имеет вид

Это выражение объясняет, почему при вращениях тел удобно пользоваться угловой характеристикой α, а не линейной величиной a. В то время как α является постоянным, a зависит от расстояния r до оси вращения.

Решение задачи на определение ускорения

Рассмотрев вопрос, что называется ускорением равноускоренного движения, решим такую задачу: автомобиль, начиная движение с места по прямой дороге, прошел за первые 10 секунд путь на 100 метров больше, чем за первые 5 секунд. С каким ускорением он двигался?

Для начала запишем рабочую формулу:

Это выражение следует из приведенной выше в статье формулы для пути при равноускоренном прямолинейном движении, если учесть, что начальная скорость v0 равна нулю.

Вычитая первое равенство из второго и подставляя значения из условия задачи, получаем:

Таким образом, за каждую секунду своего движения автомобиль увеличивал скорость на 2,67 м/с.

Источник

Ускорение при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

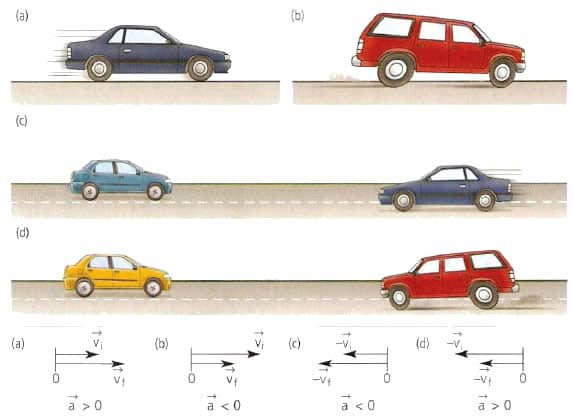
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Равноускоренное движение.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

Подставляем сюда выражение для скорости, даваемое формулой (3) :

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

Прямолинейное равноускоренное движение.

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

и подставим в формулу для перемещения:

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Рис. 1. Горизонтальный бросок

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

Источник

Равноускоренное движение

Всего получено оценок: 131.

Всего получено оценок: 131.

Одним из видов движения, изучаемых кинематикой, является равноускоренное движение. Равноускоренное движение — это достаточно распространённый вид движения, даже большинство равномерных движений начинались с разгона и были некоторое время равноускоренными. Рассмотрим эту тему подробнее, получим формулу равноускоренного движения, приведём примеры такого движения.

Ускорение

Если некоторое тело начинает движение из состояния покоя, то его скорость изменяется от нуля до некоторого максимального значения. Следовательно, при таком движении можно указать быстроту изменения скорости.

Например, в рекламе автомобилей указывается время разгона до 100 км/ч. Ясно, что модель, достигающая такой скорости за 5 секунд, значительно резвее, чем модель со временем разгона 15 секунд, хотя конечная скорость в обоих случаях одинакова. В чем же здесь разница, с точки зрения кинематики?

Из данной формулы можно получить размерность ускорения. Скорость измеряется в метрах в секунду, а время — в секундах, значит, ускорение измеряется в метрах в секунду за секунду (или метров в секунду в квадрате).

В приведённом примере первый автомобиль разгоняется с ускорением 5,56 метров в секунду за секунду, а второй — с ускорением 1,85 метров в секунду за секунду.

Рис. 1. Ускорение в физике.

Равноускоренное движение

Движение, при котором ускорение тела постоянно, называется равноускоренным. При этом знак ускорения не играет роли. Движение с постоянным отрицательным ускорением также является равноускоренным, несмотря на то, что скорость уменьшается.

Наиболее частым примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха ещё не играет большой роли. Другим примером может служить разгон автомобиля при постоянном нажатии на педаль «газа», пока не будет набрана необходимая скорость.

Формулы равноускоренного движения

Найдём формулы скорости и координаты при равноускоренном движении. Из приведённого выше определения ускорения следует, что скорость при постоянном ускорении равна:

$$\overrightarrow v= \overrightarrow + \overrightarrow a t$$

$$\overrightarrow x= <(\overrightarrow + \overrightarrow v)\over 2> t$$

Что мы узнали?

Ускорение — это физическая величина, характеризующая быстроту набора скорости материальной точкой. Движение с постоянным ускорением называется равноускоренным. Хорошим примером равноускоренного движения является свободное падение тел.

Источник

Равномерное и равноускоренное движение

В процессе такого перемещения скорость тела периодически изменяется, поэтому для описания данного процесса применяют понятия средней и мгновенной скоростей.

Мгновенная скорость – это скорость движения тела, которая фиксируется в конкретный момент времени в заданной точке пути. Другими словами, мгновенной скоростью \(v\) есть предел стремления средней скорости тела \(v_<ср>\) при бесконечно малом промежутке времени:

Известно, что предел отношения приращения функции к приращению аргумента, в случае стремления последнего к нулю, – это главная производная функции по аргументу.

Рассмотрим пример скатывания шарика по наклонной поверхности. При этом мы наблюдаем, что шарик движется неравномерно: расстояния, которые он проходит за одинаковые последовательные интервалы времени, постоянно увеличиваются. То есть, темп его движения постоянно растёт. Данное движение, как и скачивание любого предмета, является классикой прямолинейного равноускоренного перемещения.

Еще одним примером такого движения является перемещение транспорта, когда он разгоняется, а так же когда тормозит. То есть равноускоренным движением может считаться не только ускоренное, но и замедленное движение.

Дело в том, что понятие «ускорение» в физическом смысле более широкое, нежели мы привыкли использовать в ежедневной жизни. Слово ускорение в широком потреблении понимается как увеличение скорости, но физически под ускорением понимается передвижение тела с постоянным изменением скорости, при этом неважно увеличивается она или уменьшается.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Понятие прямолинейного равноускоренного движения достаточно широко используется при изучении законов механики.

Стоит отметить, что при влиянии постоянной силы тело будет перемещаться равноускорено.

Равномерное движение

Равномерное движение – это такое механическое перемещение тела, когда за равные промежутки времени оно преодолевает равные расстояния.

Для равномерного перемещения характерно постоянное значение скорости:

где \(v\) – скорость равномерного перемещения, м/с;

\(l\) – расстояние, преодоленное объектом, м;

\(δt\) – промежуток времени перемещения, с.

При равномерном перемещении скорость предмета остаётся равной на каждом промежутке пути.

Если перемещение тела не только равномерное, а также прямолинейное, то его путь равен модулю его перемещения. Значит, аналогично предыдущему выражению, определяем скорость равномерного прямолинейного перемещения:

где \(\overline \) – скорость равномерного прямолинейного перемещения, м/с;

\(\overline\) – перемещение тела, м;

\(δt\) – промежуток времени перемещения, с.

Скорость равномерного прямолинейного перемещения является векторной величиной. То есть её направление также имеет значение, как и модуль.

Равноускоренное движение тела

При равноускоренном перемещении скорость постоянно изменяется. Если речь идет об убыстрении, скорость постоянно растет. То есть ускорение остаётся величиной постоянной, а темп постоянно растет.

Помимо равноускоренного движения еще выделяют равнозамедленное, где темп постоянно уменьшается с одинаковой быстротой.

Различают одномерное и многомерное ускорение. Первое происходит вдоль одной оси координат, а второе – в плоскости или в пространстве.

Не нашли что искали?

Просто напиши и мы поможем

Ускорение тела

Формулы равномерного движения для расчета ускорения могут применяться без учёта времени в разных плоскостях. Например, при расчёте свободного падения жестких тел, можно определять их местоположение. Это бывает полезно при различных геометрических расчётах.

Неравномерное перемещение тела, так же как и равноускоренное, характеризуется изменением скорости. Но в чём же тогда их отличие? При равноускоренном – скорость тела не просто изменяется, она равно ускоряется.

Понятие ускорения часто ассоциируют с ростом скорости. Поскольку скорость растет одинаково, говорят о равном возрастании скорости. Как же определить, скорость растет равномерно или нет? Для этого засекают время, оценивают приращение скорости за равные промежутки времени, если при этом приращение одинаково на каждом новом участке, передвижение считается равноускоренным.

Ускорение – это физическая величина, показывающая на сколько возрастает скорость.

Замедленным движением есть перемещение с уменьшающейся скоростью. Поскольку в физике любое перемещение с меняющейся скоростью называется ускоренным, то неважно разгоняется автомобиль либо тормозит, в любом случае он передвигается с ускорением.

Значит, ускорение описывает быстроту изменения скорости. Оно показывает на сколько меняется скорость за одну секунду. Чем больше величина ускорения, тем стремительнее тело набирает скорость либо сбрасывает её. Ускорение обозначается буквой a и определяется соотношением изменения скорости δv к промежутку времени δt, за которое оно осуществлено:

Источник