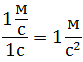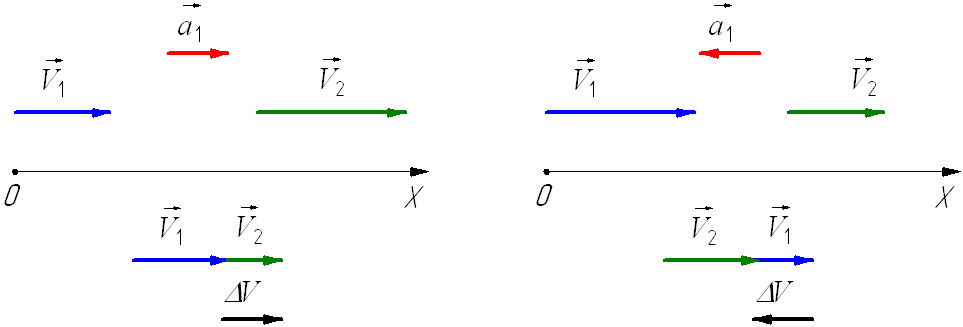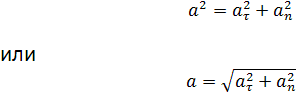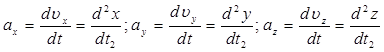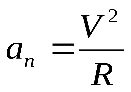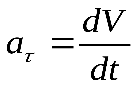Что называется ускорением материальной точки
Тема 1.7. Ускорение точки и его виды
§1. Вектор ускорения точки
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.
Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v, а в момент t 1 приходит в положение M 1 и имеет скорость v 1 (рис. 1).
Рис.1. Движение точки М с ускорением
Отношение приращения вектора скорости к соответствующему промежутку времени ∆t определяет вектор среднего ускорения точки за этот промежуток времени:
Ускорение точки равно нулю лишь тогда, когда скорость точки v постоянна как по величине, так и по направлению: это соответствует только прямолинейному и равномерному движению.
Найдем, как располагается вектор по отношению к траектории точки. При прямолинейном движении вектор направлен вдоль прямой, по которой движется точка.
При прямолинейном движении с возрастающей по модулю скоростью (рис. 2, а) векторы и сонаправлены () и проекция ускорения на направление движения положительна.
При прямолинейном движении с убывающей по модулю скоростью (рис. 2, б) направления векторов и противоположны () и проекция ускорения на направление движения отрицательна.
Ускорение материальной точки

Всего получено оценок: 169.
Всего получено оценок: 169.
Большинство движений в Природе являются неравномерными, они происходят с ускорением или замедлением. Рассмотрим понятие «ускорение материальной точки» более подробно.
Неравномерное движение
При равномерном движении материальная точка проходит за одинаковые промежутки времени одинаковые расстояния, и измерение скорости на любом участке дает одно и то же значение.
При неравномерном движении ситуация иная. Измерение скорости в различные моменты времени дает различные результаты. Нередок случай, когда мгновенная скорость в любой точке пути отличается от мгновенной скорости в любой другой точке. Возникает вопрос определения не только координаты, но и скорости в каждый момент времени и в каждой точке пути для неравномерного движения.
Ускорение
Для исследования свободного падения можно измерять мгновенную скорость через равный промежуток времени (например, через 0.1с), и результаты представить в виде таблицы. В первом столбце будет момент времени, во втором – мгновенная скорость. В третьем столбце вычислим разницу мгновенной скорости между текущим и предыдущим моментом времени.
t(сек)
Δv(м/с)
Сразу бросается в глаза, что цифры в последнем столбце таблицы одинаковы. Это означает, что, хотя скорость постоянно меняется, разница скорости за одинаковый промежуток времени составляет одинаковую величину. Следовательно, для вычисления скорости в любой момент времени можно ввести специальную меру – ускорение.
Ускорение материальной точки равно отношению изменения скорости материальной точки к промежутку времени, за который это изменение произошло.

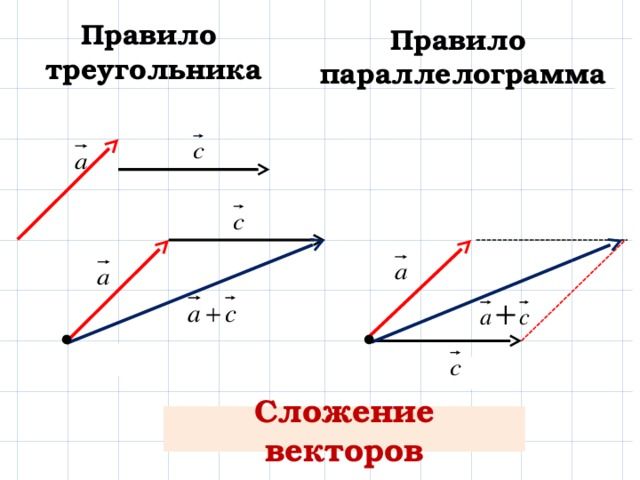
Также из этой формулы видно, что ускорение – это векторная величина, и направление ускорения материальной точки совпадает с направлением изменения скорости. При этом и величину, и направление этого изменения необходимо получать с помощью правил сложения векторов. В частности, если конечная скорость больше начальной, и направлена в том же направлении, то и ускорение будет направлено туда же. Если конечная скорость меньше начальной, то ускорение будет направлено в противоположную сторону. В случае, если вектора начальной и конечной скоростей не параллельны, для определения результата следует либо пользоваться правилом параллелограмма, либо проецировать вектора на оси координат, и складывать или вычитать проекции в зависимости от их направления, а потом по проекциям получать результат.
Что мы узнали?
При неравномерном движении скорость тела изменяется. Для характеристики быстроты этого изменения вводится специальная величина – ускорение. Ускорение равно отношению изменения скорости за некоторый промежуток времени к величине этого промежутка.
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
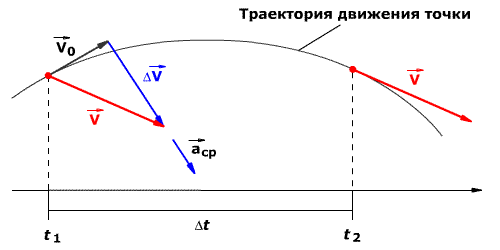
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 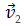
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 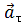
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 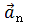
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
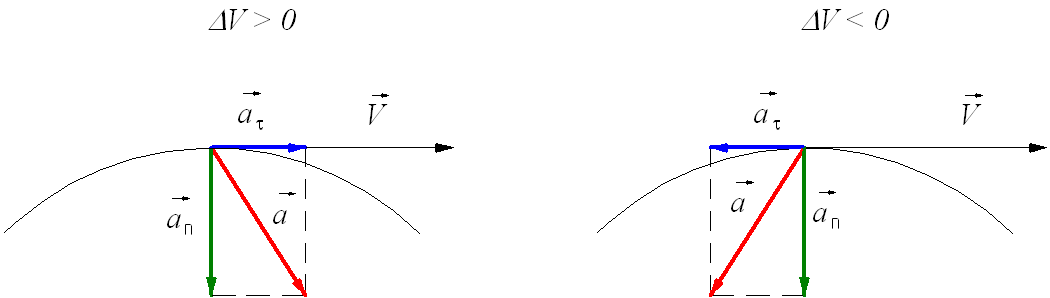
Направление полного ускорения также определяется правилом сложения векторов:
Ускорение материальной точки
Ускорение 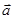
Отношение изменения вектора скорости к промежутку времени Δt, за которое это изменение произошло, называется вектором среднего ускорения:
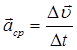
Мгновенное ускорение материальной точки равно первой производной от скорости по времени или второй производной от радиуса вектора 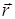
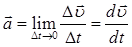
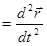
Единица измерения ускорения [а]= 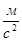
Следует также отметить, что вектор ускорения 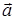
Проекции вектора 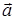
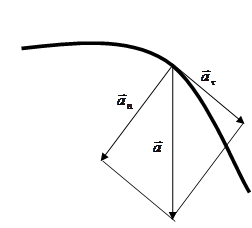
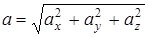
Пусть точка совершает криволинейное движение. Вектор ускорения в этом случае можно представить в виде суммы двух проекций: 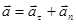

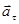
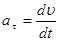
Нормальное (центростремительное) ускорение 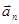
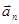
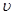
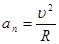
Величина полного ускорения:
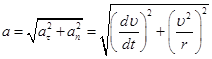
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
1. 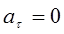
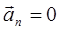
2. 
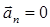
Если 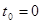
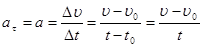
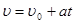
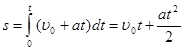
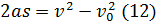
Если начальная скорость υ0=0, то формулу пути 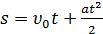
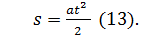
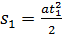
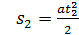
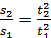
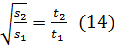
3. 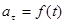

4. 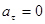
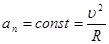
5. 
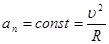
6. 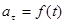
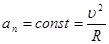
7. 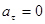
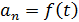
8. 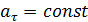
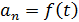
9. 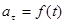
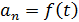
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. Измерение средней и мгновенной скоростей неравномерного движения
Опыт 1
1. Установка для выполнения опыта схематически изображена на рисунке 6.


2. Установите датчики на наклонной части желоба: первый датчик разместите на нулевой отметке шкалы, а второй датчик на расстоянии 20 см от первого (см. рис.6).
3. Освободите шарик и измерьте не менее трех раз промежутки времени, в течение которых шарик двигался между оптическими датчиками.
4. Повторите измерения, каждый раз уменьшая расстояние между датчиками на 4 см (по 2 см с каждой стороны), так, чтобы середина отрезка между датчиками располагалась в точке желоба, при прохождении которой требуется найти мгновенную скорость (на расстоянии 10 см от нулевой отметки шкалы). При последнем измерении датчики должны находиться на минимальном расстоянии друг от друга.
7. Рассчитайте значения средней скорости шарика по формуле 1 при различных расстояниях между датчиками. Результаты измерений и вычислений занесите в таблицу.
Таблица 1 – Определение средней скорости
| № п/п | x1 | x2 | Δr | Δt | υср |
8. Подсоедините оптический датчик к гнезду 1 секундомера, включите секундомер и установите прибор в режим (ONE).
9. Установите датчик на наклонной части желоба на расстоянии 10 см от нулевой отметки шкалы.
10. Освободите шарик, установленный в пусковом устройстве, и измерьте промежуток времени, в течение которого шарик перекрывал световой пучок, излучаемый светодиодом, двигаясь в створе оптического датчика (диаметр шарика d =22 мм).
11. Рассчитайте модуль скорости шарика (для расчета достаточно разделить диаметр шарика на измеренный промежуток времени) и сравните полученный результат с последним результатом измерений мгновенной скорости двумя датчиками.
Опыт 2.
1. 
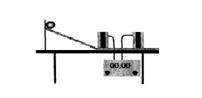
2. Для определения средней и мгновенной скорости шарика при его движении на горизонтальном участке желоба, установите датчики на расстоянии 10 см друг от друга на горизонтальной части желоба так, чтобы середина отрезка между датчиками располагалась около точки желоба, при прохождении которой требуется найти мгновенную скорость.
3. Установите шарик в пусковое устройство.
5. Освободите шарик и не менее трех раз измерьте промежутки времени, в течение которых шарик двигался между оптическими датчиками.
6. Повторите измерения, каждый раз уменьшая расстояние между датчиками на 4 см (по 2 см с каждой стороны). При последнем измерении разместите датчики на минимальном расстоянии друг от друга.
7. Вычислите значения средней скорости шарика по формуле 1для различных расстояний между датчиками, с точностью до 0.01.
8. Результаты измерений и вычислений занесите в таблицу 2.
Таблица 2 – Вычисление значения средней скорости шарика для различных расстояний между датчиками
| № п/п | x1 | x2 | Δr | Δt | υср |
9. Измерьте модуль скорости шарика на горизонтальном участке желоба, используя один датчик, и сравните полученные результаты с результатами измерений скорости двумя датчиками.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
.Нормальное ускорение– векторная физическая величина, характеризующая изменение направления скорости, численно равная отношению квадрата скорости к радиусу кривизны траектории, направленная вдоль радиуса кривизны к центру кривизны:

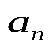
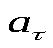







24. Что называется тангенциальным ускорением материальной точки, как его вычислить? –
Тангенциальное ускорение– векторная физическая величина, характеризующая изменение скорости тела по абсолютному значению, численно равная первой производной от модуля скорости по времени и направленная по касательной к траектории в ту же сторону, что и скорость, если скорость возрастает, и противоположно скорости, если она убывает.

25. Напишите формулу для определения полного ускорения материальной точки. –
Импульс
Единицы измерения
Ньютон (обозначение: Н) — единица измерения силы в СИ. Принятое международное название — newton (обозначается N).
Ньютон — производная единица. Исходя из второго закона Ньютона, она определяется как сила, сообщающая телу массой 1 кг ускорение 1 м/с² в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с2
Единицы измерения СИ кг/м³.
Дата добавления: 2019-09-13 ; просмотров: 2138 ; Мы поможем в написании вашей работы!