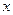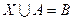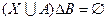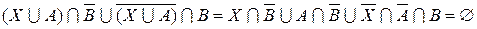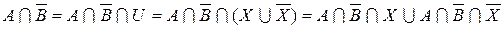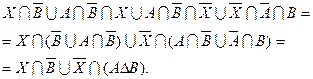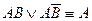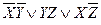Что называется уравнением множества

Решение уравнений алгебры множеств

Пусть дано уравнение вида:

(23)

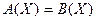
Алгоритм решения уравнений алгебры множеств имеет следующий алгоритм:

1. Представляем данное уравнение в следующем виде:

(24)

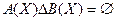
2. Используя алгебру множеств, преобразуем данное уравнение к виду:

(25)

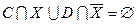
3. Решением уравнения является следующее выражение:

(26)

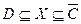
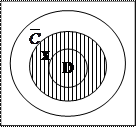Рис 2. Диаграмма Эйлера-Венна для решения уравнения алгебры множеств.

Необходимо решить уравнение:

1. Преобразуем данное уравнение:

2. С помощью алгебры множеств преобразуем данное выражение следующим образом:

C учетом данных преобразований имеем:

Таким образом, имеем множества C и D в следующем виде:

.

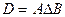
Решением уравнения будет множество:

.

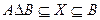
Решение уравнения (один из вариантов) может быть представлено на диаграмме Эйлера-Венна

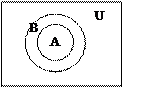Рис 3 Диаграмма Эйлера-Венна для решения уравнения алгебры множеств.

При изображении решения уравнения алгебры множеств следует иметь в виду, что два множества могут иметь следующие диаграммы Эйлера-Венна

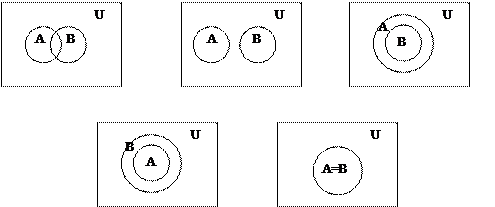Рис 4 Диаграмма Эйлера-Венна для решения уравнения алгебры множеств.

Источник

Решение уравнений алгебры множеств.

Теория множеств.

Множеством Sназывается объединение в одно целое объектов, хорошо различимых нашей мыслью или интуицией. Эти объекты называется элементами множества S. Такое интуитивное определение дал немецкий математик Г. Кантор. В данном определении важны следующие два момента:

1. Множество- это нечто, состоящее из хорошо различимых объектов.

2. Это нечто мыслится как единое целое.

Множества могут быть заданы следующими способами:

1. перечислением (списком своих элементов);

2. описанием свойств, которыми должны обладать его элементы;

3. порождающей процедурой.

Множество экзаменационных оценок может быть задано:

2. описанием свойств: А=

3. порождающей процедурой: А= <а| а=2+i, i= >

Подмножеством множества А называется множество В, если любой элемент множества В принадлежит множеству А:

(1)

Символом Í обозначается отношение включения. Запись АÍВ означает множество А является подмножеством множества В.

Не следует смешивать отношение принадлежности Î и отношение включения Í. Отношение принадлежности применяется к элементам множества, а отношение включения к множествам. Хотя 1Î<1>,<1>Î<<1>>, не верно, что 1Î<<1>>, так как единственным элементом множества <<1>> является <1>.

Если АÍB и A¹B, то AÌB, то есть множество А строго включено в множество В. Символ Ì называется строгим включением.

Свойства подмножеств.

1. Рефлексивность. Множество А является подмножеством множества А:

. (2)

(3)

3. Принцип объемности. Если множество А является подмножеством множества В, а множество В является подмножеством множество А, то множество А равно множеству В:

(4)

Операции над множествами.

1. Объединением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В:

(5)

2. Пересечениеммножеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат множеству А и множеству В:

(6)

3. Разностьюмножества А и В называется множество всех тех элементов, которые принадлежат множеству А и не принадлежат множеству В:

(7)

(8)

5. Дополнениеммножества А называется множество всех тех элементов, которые не принадлежат множеству А:

(9)

Для наглядного представления операций над множествами используют диаграммы Эйлера- Венна.

Рис 1. Диаграмма Эйлера-Венна

где — это области 1,2,3

— это область 3;

— это область 1;

— это область 1,3

— это области 2,4.

Алгебра теории множеств.

Для любых множеств А, В и С выполнимы следующие тождества:

1. Коммутативный закон

(9)

2. Ассоциативный закон

(10)

3. Дистрибутивный закон

(11)

4. Закон поглощения

(12)

5. Закон идемпотентности

(13)

6. Закон де Моргана

(14)

7. Закон исключенного третьего

(15)

8. Закон противоречия

(16)

9. Операции с универсумом:

(17)

10. Операции с пустым множеством:

(18)

11. (19)

12. Закон двойного дополнения

(20)

13. (21)

14. (22)

При преобразованиях выражений над множествами по законам алгебры логики существуют следующие приоритеты: самой приоритетной операцией является дополнение, затем пересечение и в последнюю очередь объединение.

Кортеж.

Проекцией кортежа на i-тую осьназывается его i-тая компонента.

Проекцией кортежа на пустое множество осей является пустой кортеж.

Пр А₅ не определена

Пр А_4,2 не определена.

Проекция множества.

Проекция множества определена только для множеств, элементами которого являются кортежи одинаковой длины.

Проекцией множестваназывается множество проекций соответствующих кортежей.

Пр А_3,1 не определена.

График и свойства графика

Графиком называется множество пар. Графики могут задаваться :

1. перечислением:

2. описанием свойств:

График называется симметричным, если вместе с каждой парой он содержит её инверсию.

(27)

Диагональнымназывается график вида:

, (28)

Композицией графиков называется график R, такой что для любой пары ÎR есть такой элемент z, что ÎP, а ÎQ.

, (29)

P Q=<;;; ; >.

2. Пусть заданы графики P и Q:

Рис 5. Композиция графиков.

Свойства графиков.

Функциональным графиком называется график, который не содержит пары с одинаковыми первыми и различными вторыми компонентами.

Инъективным графикомназывается график, который не содержит пары с одинаковыми вторыми и различными первыми компонентами.

Рис 6. Примеры графиков.

P1-График функциональный, но не инъективный.

P2-График инъективный, но не функциональный.

P3- График функциональный и инъективный.

Возможно другое изображение графиков.. Пусть 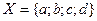, а

P1-График функциональный, но не инъективный.

P2-График инъективный, но не функциональный.

P3- График функциональный и инъективный.

Соответствия.

Соответствием называется тройка вида 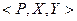. При этом — область отправления (определения), — область прибытия (значений), — график соответствия.

Рис. 9 График соответствия.

Если , то данное соответствие называется полным.

Если , то данное соответствие называется пустым.

Свойства соответствий.

1. Соответствие называется функциональным, если его график функционален.

2. Соответствие называется инъективным, если его график инъективен.

3. Соответствие называется всюду определенным, если проекция его графика на первую ось совпадает с областью отправления. Пр P₁=X.

4. Соответствие называется сюръективным, если проекция его графика на вторую ось совпадает с областью прибытия. Пр P₂=Y.

5. Соответствие называется биективным (взаимнооднозначным), если оно функционально, инъективно, всюду определенно, сюръективно.

Дано соответствие

1. функциональное, так как две и более конфет не может быть упаковано в один фантик;

2. инъективное, так как одна конфета не может быть завернута в два антика одновременно (брак упаковочной техники не рассматривается);

3. не всюду определенное, так как существуют сорта конфет, которые продаются без фантиков (зефир, мармелад);

5. не биективное, так как является несюръективным соответствием.

Отношения.

Пусть дано , где , а график отношения определяется как . Это отношение ”X больше Y” на множестве натуральных чисел. Данное отношение задано описанием свойств. Перечислением данное отношение может быть задано следующим образом:

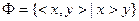
Отношение называется отношением равенства, если F=DM=< ; ;¼>.

Отношение называется отношением неравенства, если F=M 2 \DM.

Запись xjy означает, что между x и y существует отношение j.

Операции над отношениями.

3. дополнение `

Антирефлексивность.

Отношение называется антирефлексивным, если для всех x выполняется условие: ùxjx (символ “ù“ означает “не выполняется”) или .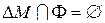

3. Симметричность.

Антисимметричность.

Отношение называется антисимметричным, если для всех x выполняется условие: xjy и x¹y Þù yjx или ÍDM.

Асимметричность.

Отношение называется асимметричным, если для всех x выполняется условие: xjy Þù yjx или =Æ.

6. Связность (полнота).

Отношение называется связным (полным), если для всех x выполняется условие: x¹y Þ xjy или yjx или М 2 \DMÍ .

Транзитивность.

Отношение называется транзитивным, если для всех x выполняется условие: xjy и yjz Þ xjz или Ф ФÍФ.

— рефлексивным, так как DXÍФ;

— антисимметричным, так как ÍDX;

— транзитивным, так как Ф Ф=< ;;; >ÍФ;

Отношение называется отношением эквивалентности, если оно рефлексивное, симметричное и транзитивное.

Отношение называется отношением нестрогого (частичного) порядка( ) ,если оно рефлексивное, антисимметричное и транзитивное.

Отношение называется совершенно нестрого порядка( ),если оно рефлексивное, антисимметричное, транзитивное и связное.

Отношение называется строго порядка( ),если оно антирефлексивное, антисимметричное и транзитивное .

Отношение называется совершенно строго порядка( ),если оно антирефлексивное, транзитивное и связное.

Решетки.

Диаграммы Хассе.

Рассмотрим отношение частичного порядка: “быть подмножеством“ на множестве-степени М=<1,2>.

Графически данное отношение можно изобразить следующим образом:

РИС 10 Графическое изображения отношения

Для отношений частичного порядка применимы диаграммы Хассе, которые строятся на основе обыкновенной диаграммы следующим образом:

1. рефлексивные петли и транзитивные связи не изображаются;

2. большие элементы ( элементы, в которые входят стрелки) располагают выше.

Таким образом, диаграмма Хассе для вышеприведенного примера будет выглядеть следующим образом:

РИС 11 Диаграмма Хассе

Для частично упорядоченного множества справедливо следующее:

4. Множество мажорант В образует верхнюю границу множества В. Множество минорант В образует нижнюю границу множества В.

5. Наименьший элемент верхней границы называется точной верхней границей, илиsupremum ( sup ) B. Наибольший элемент нижней границы называется точной нижней границей, или infimum (inf) B.

Пусть дано отношение, представленное на диаграмме Хассе

РИС 12 Диаграмма Хассе

Отношение А не является решеткой, т.к. элементы 7 и 8 не имеют sup.

Отношение В является решеткой, т.к. любая пара имеет sup и inf.

Математическая логика

Формулы равносильности.

АV(ВVС) º (АVВ)VС А&(В&С) º (А&В) &С

АV(В&С) º (АVВ)&(АVС) А&(ВVС) º (А&В)V(А&С)

6) Закон де Моргана

º & º V

7) Закон исключающий третьего

8) Закон противоречия

9) Закон двойного отрицания

º A

11) A®B º VB

13) AÅB º A& V &B

14) A | B º º V

15) A¯B º º &

Доказать:

Представление произвольной функции алгебры логики в виде формулы алгебры логики

Пусть — произвольная функция алгебры логики переменных.

(2.1)

которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции при некоторых определенных значениях переменных , остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0..

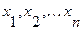
Вместе с тем формула (2.1) содержит в виде логических слагаемых всевозможные конъюнкции указанного вида.

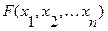
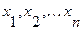
Ясно, что формула (2.1)полностью определяет функцию . Иначе говоря, значения функции и формулы (2.1) совпадают на всех наборах значений переменных . То есть функция

Составление формул по таблице истинности. 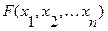может быть представлена в виде:

(2.2)

ПРИМЕР Пусть функция имеет следующую таблицу истинности:

Тогда функция может быть определена в следующем виде:

Нетрудно заметить, что для определении функции берутся только те наборы переменных , при которых функция принимает значения 1, что значительно упрощает процедуру определения функции .

Формула (2.1) обладает свойствами:

2. Все логические слагаемые формулы различны.

3. Ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание.

4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

5. Перечисленные свойства называются свойствами совершенства.

Метод Квайна.

Алгоритм метода Квайна включает в себя следующие этапы:

1. Любая формула приводится к СДНФ.

2. СДНФ приводится к сокращенной ДНФ (СкДНФ). При получении СкДНФ используются следующие формулы равносильности:

а) Формула склеивания

б) Формула неполного склеивания

в) Формула поглощения

Применяя все возможные процедуры склеивания, СДНФ приводится к СкДНФ.

Необходимо найти МДНФ формулы:

Осуществляем всевозможные склеивания

1-2

1-4

2-3

3-6

4-5

5-6

Составляем импликантную матрицу

	+	+
	+	+
	+	+
	+	+
	+	+
	+	+

По данной импликантной матрице можно выбрать следующие МДНФ

Метод минимизирующих карт.

Алгоритм метода минимизирующих карт включает в себя следующие этапы:

1. Любая формула приводится к СДНФ.

2. Составляется таблица всевозможных сочетаний переменных.

3. Из таблицы вычеркиваются те строки, которые не содержат конституенты СДНФ. Конъюнкции этих строк вычеркиваются в других строках.

4. В каждой строке оставляются конъюнкции с минимальным количеством переменных.

5. Из каждой строки выбирается олна конъюнкция и составляется ДНФ.

6. Из построенных ДНФ выбирается минимальная.

							*
							*

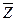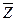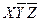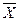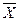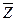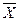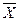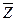После соответствующих преобразований получаем следующую таблицу

*
*

После всевозможного перебора остаются следующие МДНФ:

Логика предикат.

Предикатом является высказывание – быть четным числом на множестве натуральных чисел:

— быть четным числом;

Квантовые операции.

Для предикатов кроме логических операций применимы кванторные операции: всеобщности и существования.

Пусть — предикат, определенный на множестве . Тогда — означает «для всякого (любого) истинно ». Символ называется квантором всеобщности.

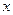
Переменную в предикате называют свободной ( ей можно придавать различные значения из М), в высказывании

Источник