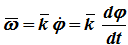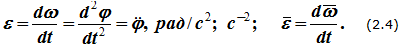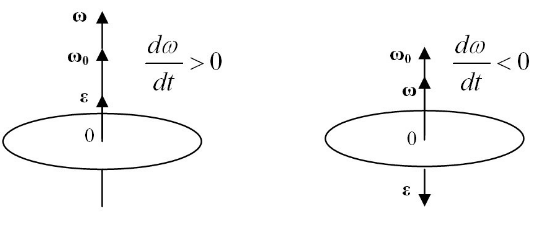Что называется угловым ускорением

Формула для вычисления углового ускорения

Угловое ускорение – что это?

Угловое ускорение \(\varepsilon\) – физическая величина, характеризующая изменение угловой скорости при движении тела.

Единица измерения: \(\lbrack\varepsilon\rbrack=\frac1<с^2>\) или \(с^<-2>\)

Угловая скорость

Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Угловая скорость \(\omega\) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.

При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).

Вектор угловой скорости направлен вдоль оси вращения.

Основные формулы для вычисления угловой скорости

Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):

Единица измерения угловой скорости в СИ: \(\lbrack\omega\rbrack=\frac<рад>с\)

Связь между угловой скоростью и нормальным (центростремительным) ускорением

Центростремительное (нормальное) ускорение \(a_n\) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.

Центростремительное ускорение определяется по формуле:

где \(V\) – скорость движения, \(R\) – радиус окружности.

Единица измерения в СИ: \(\lbrack a_n\rbrack=\frac м<с^2>\)

Итак, формула связывающая эти две величины:

Основные формулы для расчета углового ускорения

Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.

Угловое ускорение маховика

Среднее угловое ускорение

Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.

Тангенциальное ускорение

Тангенциальным (касательным) ускорением \(a_\tau\) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.

Мгновенное угловое ускорение

Мгновенное угловое ускорение \(\alpha\) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.

Источник

iSopromat.ru

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела:

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

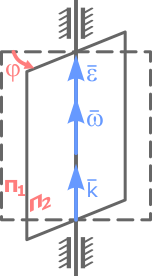
Быстрота изменения угла φ (перемещения из положения П₁ в положение П₂) – это и есть угловая скорость:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

Приняв k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Угловое ускорение

Смотреть что такое «Угловое ускорение» в других словарях:

Угловое ускорение — Размерность T−2 Единицы измерения СИ рад*с−2 СГС … Википедия

УГЛОВОЕ УСКОРЕНИЕ — УГЛОВОЕ УСКОРЕНИЕ, степень изменения угловой скорости. Средняя величина углового ускорения предмета, угловая скорость которого изменяется от q1 до q2 за время t, выражается как (q1 q2)/t. Мгновенным угловым ускорением называется величина,… … Научно-технический энциклопедический словарь

УГЛОВОЕ УСКОРЕНИЕ — УГЛОВОЕ УСКОРЕНИЕ, величина, характеризующая быстроту изменения угловой скорости твердого тела. При вращении тела вокруг неподвижной оси, когда его угловая скорость w растет (или убывает) равномерно, абсолютная величина углового ускорения e=Dw/Dt … Современная энциклопедия

УГЛОВОЕ УСКОРЕНИЕ — величина, характеризующая быстроту изменения угловой скорости твёрдого тела. При вращении тела вокруг неподвижной оси, когда его угловая скорость w растёт (или убывает) равномерно, численно У. у. e=Dw/Dt, где Dw приращение, к рое получает w за… … Физическая энциклопедия

УГЛОВОЕ УСКОРЕНИЕ — величина, характеризующая быстроту изменения угл. скорости твёрдого тела. При вращении тела вокруг неподвижной оси, когда его угл. скорость w растёт (или убывает) равномерно, численно У. у. e = dw/dt, где dw приращение, к рое получает w за… … Физическая энциклопедия

угловое ускорение — Мера изменения угловой скорости тела, равная производной от угловой скорости по времени. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики… … Справочник технического переводчика

Угловое ускорение — УГЛОВОЕ УСКОРЕНИЕ, величина, характеризующая быстроту изменения угловой скорости твердого тела. При вращении тела вокруг неподвижной оси, когда его угловая скорость w растет (или убывает) равномерно, абсолютная величина углового ускорения e=Dw/Dt … Иллюстрированный энциклопедический словарь

угловое ускорение — векторная величина, характеризующая быстроту изменения угловой скорости твердого тела. При вращении тела вокруг неподвижной оси, когда его угловая скорость ω растёт (или убывает) равномерно, абсолютная величина углового ускорения ε = Δω/Δt, где… … Энциклопедический словарь

угловое ускорение — kampinis pagreitis statusas T sritis automatika atitikmenys: angl. angular acceleration vok. Winkelbeschleunigung, f rus. угловое ускорение, n pranc. accélération angulaire, f … Automatikos terminų žodynas

угловое ускорение — kampinis pagreitis statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis dydis, lygus kampinio greičio pokyčiui per vienetinį laiko tarpą, t. y. α = dω/dt; čia dω – kampinio greičio pokytis, dt – laiko tarpas. atitikmenys: angl.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

Угловое ускорение

Угловое ускорение – это псевдовекторная физическая величина, которая равна первой производной от псевдовектора угловой скорости по времени:

.

Угловое ускорение характеризует силу изменения модуля и направления угловой скорости при движении твердого тела.

Ускорение точки твердого тела при свободном движении.

К понятию углового ускорения можно прийти, изучая определение ускорения точки твердого тела, находящегося в свободном движении. Определение скорости точки тела В (по формуле Эйлера) в свободном движении:

.

где — скорость точки тела А, которая была принята как полюс; — псевдовектор угловой скорости тела; — вектор, который был выпущен из полюса в точку – его скорость определяем. Продифференцировав это выражение по времени данное выражение, получаем:

.

где — является ускорением полюса А; — псевдовектором углового ускорения.

Составляющая ускорения точки В, которая определяется через угловое ускорение называется вращательным ускорением точки В около полюса А.

.

Последнее слагаемое в полученной формуле, которое зависит от угловой скорости, называется осестремительным ускорением точки В вокруг полюса А.

.

Угловое ускорение при вращении тела вокруг неподвижной оси.

Когда происходит вращение тела около неподвижной оси, которая проходит через недвижимые точки тела О₁ и О₂, производные орта оси вращения = 0:

.

Отсюда вектор углового ускорения вычисляется тривиально через вторую производную угла поворота

или .

где — это алгебраическая величина углового ускорения.

Здесь псевдовектор углового ускорения (и угловая скорость) идет по оси вращения тела. В случае наличия одинакового знака у первой и второй производной угла поворота:

,

значит, вектор углового ускорения и вектор угловой скорости имеют одинаковое направление и тело имеет ускоренное вращение. Иначе, при , векторы угловой скорости и углового ускорения имеют противоположные направления, а, значит, тело вращается замедленно.

В теормехе обычно вводится понятие угловой скорости и углового ускорения, когда рассматривается вращение тела вокруг не двигающейся оси. При чем, для решения задачи используют зависимость от времени угла поворота тела

Отсюда закон движения точки тела можно выразить натурально, как длина дуги окружности, которую прошла точка, совершая поворот тела от определенного исходного положения φ₀ = φ (t₀)

где R является расстоянием от точки до оси вращения.

Продифференцировав вышеуказанное выражение по времени, найдем алгебраическую скорость точки:

.

где является алгебраической величиной скорости угловой.

Через геометрическую сумму тангенциального и нормального ускорения можно выразить ускорение точки тела при вращении:

.

При этом тангенциальное ускорение выходит в виде производной от алгебраической скорости точки:

.

где является алгебраической величиной углового ускорения. А при помощи ниже приведенной формулы определим нормальное ускорение точки тела:

.

Источник

Угловое ускорение

Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.

Основные понятия

Угловое ускорение – величина, характеризующая изменение скорости с течением времени.

Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.

Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.

Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.

В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.

Закон равнопеременного вращения

Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:

Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.

Вращение является равнозамедленным, когда ω и ε противоположны по знаку.

Практические примеры

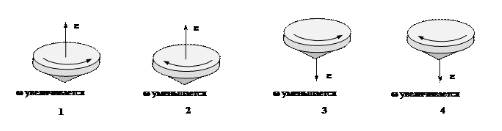
На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.

Запишем выражения для угловой скорости и углового ускорения заданной точки:

Полное ускорение запишем как:

Источник